NCERT Exemplar Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry and its Equation Exercise 8.3

Chapter 8 Introduction to Trigonometry and its Equation NCERT Exemplar Solutions Exercise 8.3 Class 10 Maths

Chapter Name	NCERT Maths Exemplar Solutions for Chapter 8 Introduction to Trigonometry and its Equation Exercise 8.3
Book Name	NCERT Exemplar for Class 10 Maths
Other Exercises	Exercise 8.1 Exercise 8.2 Exercise 8.4
Related Study	NCERT Solutions for Class 10 Maths

Exercise 8.3 Solutions

Short Answer Questions

Prove the following (from Q.1  to Q.7):

1. Sinθ/(1 + cosθ) + (1 + cosθ)/sinθ = 2cosecθ

Solution

L.H.S = 

Hence proved.

2. tanA/(1 + secA) - tanA/(1 - secA) = 2cosecA

Solution

L.H.S 

As,
sec²A – tan²A = 1
⇒ sec²A – 1  = tan²A
= R.H.S
Hence proved.

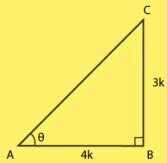
3. If tan A = 3/4, then sin A cos A = 12/25 

Solution

As given in the question, 
tan A = 3/4 
Also, 
tan A = Perpendicular/Base 
So, 
tan A = 3k/4k
Where, 
Perpendicular = 3k
Base = 4k 

Using Pythagoras Theorem,
(hypotenuse)² = (perpendicular)² + (base)² 
⇒ (hypotenuse)² = (3k)² + (4k)² 
= 9k² + 16k² 
= 25k² 
hypotenuse = 5k
Now find sin A and cos A, 
sin A = 3k/5k
= 3/5
cos A = 4k/5k
= 4/5
So, 
sin A cos A = 3/5 × 4/5 
= 12/25
Hence, proved. 

4. (sinα + cosα)(tanα + cotα) = secα + cosecα

Solution

L.H.S: 
(sinα + cosα) 
So, 
 (sinα + cosα)(tanα + cotα) 

secα + cosecα 
= R.H.S 
Hence, proved.

5. (√3 + 1)(3 - cot30°) = tan³ 60° - 2sin60°

Solution

(√3 + 1)(3 - cot30°)
= (√3 + 1)(3 - √3)
[as, cot 30° = √3]
= (√3 + 1) √3(√3 - 1)
[ as, (3 - √3) = √3(√3 - 1)]
= [(√3)2 - 1]√3
[as, (√3 + 1)(√3 - 1) = [(√3)² - 1]
= (3 - 1)√3
= 2√3
Also, solving
R.H.S : 
tan³ 60° - 2sin 60°
As, 
tan 60° = √3 and 
sin 60° = √3/2, 
we get, 
(√3)3 - 2(√3/2) = 3√3 - √3 = 2√3
So, 
L.H.S = R.H.S 
Hence, proved.

6. 1 + cot² α/(1 + cosec α) = cosec α

Solution

Taking LHS, 

7. tan θ + tan (90° - θ) = sec θ sec(90 - θ)

Solution

L.H.S = tan (90° - θ) = cot θ
tan θ + tan (90 - θ) = tan θ + cot(θ) 

= sec θ cosec θ
= sec θ sec(90 - θ)
Hence proved.

8. Find the angle of elevation of the sun when the shadow of a pole h metres high is √3h metres long. 

Solution

Let the angle of elevation of the Sun is θ.

Given, height of pole = h m

Now, in ∆ABC,

tan θ = 1/√3
= tan 30°
θ = 30°
So, the angle of elevation of the Sun is 30°.

9. If √3 tan θ = 1, then find the value of sin²θ - cos²θ.

Solution
Given, 
√3 tan θ = 1,
⇒ tanθ = 1/√3
⇒ tanθ = tan 30°
 θ = tan 30° 
So, 
sin² θ - cos² θ = sin² 30° - cos² 30°
= (1/2)² - (√3/2)² 
= -1/2 

10. A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.

Solution

Given,

height of the ladder = 15 m

Let the height of the vertical wall = h

Because, and the ladder makes an angle of 60° with the wall i.e., θ = 60°

In ∆QPR,

cos60° = PR/PQ 
1/2 = h/15 
h = 15/2 m

11. Simplify (1 + tan² θ)(1 - sinθ)(1 + sinθ) 

Solution

(1 + tan² θ)(1 - sinθ)(1 + sinθ)
= (1 + tan² θ)(1 - sin² θ)  [as, (a - b)(a + b) = a² - b²]
= sec² θ.cos² θ  [as, 1 + tan² θ= sec² θ and cos² θ + sin² θ = 1]

= (1/cos² θ).cos² θ
= 1  [as, sec θ = 1/cosθ]

12. If 2 sin² θ - cos² θ = 2, then find the value of θ.

Solution

Given, 2 sin² θ - cos² θ = 2
2 sin² θ - (1 - sin² θ) = 2  [as, sin² θ + cos² θ = 1]
⇒ 2sin² θ - sin² θ - 1 = 2
⇒ 3sin² θ = 3 
⇒ sin² θ = 1
⇒ sinθ = 1 = sin90°  [as, sin 90° = 1]
⇒ θ = 90°

13. Show that [cos² (45° + θ) + cos² (45° - θ)/tan(60° + θ)tan(30° - θ) = 1 

Solution

14. An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.

Solution

Let the angle of elevation of the top of the tower from the eye of the observer is θ 
Given that, 

AB = 22m,

PQ = 1.5 m = MB

and

QB = PM = 20.5 m

Also,

AM = AB - MB

22 - 1.5 = 20.5 m

Now in ∆APM,

tanθ = AM/PM

=20.5/20.5

=1

= tan45°

tanθ = tan45°

⇒ θ = 45°

Hence, the required angle of elevation of the top of the tower from the eye of the observer is

45°.

15. Show that tan⁴ θ + tan² θ = sec⁴ θ - sec² θ.

Solution

LHS = tan⁴ θ + tan² θ
= tan² θ(tan² θ + 1)
= tan² θ.sec² θ  [as, sec² θ = tan² θ + 1]
= (sec² θ - 1).sec² θ  [as, tan² θ = sec² θ - 1]
= sec⁴ θ - sec² θ

= RHS