NCERT Exemplar Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Exercise 7.4

Chapter 7 Coordinate Geometry NCERT Exemplar Solutions Exercise 7.4 Class 10 Maths

Chapter Name	NCERT Maths Exemplar Solutions for Chapter 7 Coordinate Geometry Exercise 7.4
Book Name	NCERT Exemplar for Class 10 Maths
Other Exercises	Exercise 7.1 Exercise 7.2 Exercise 7.3
Related Study	NCERT Solutions for Class 10 Maths

Exercise 7.4 Solutions

Long Answer Questions

1. If (-4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.

Solution
Let us take the vertices be (x, y) 

Distance between (x, y) & (4, 3) is = √((x-4)² + (y-3)²) ...(1)
Distance between (x, y) & (-4,3) is = √((x+4)² + (y-3)²)  ...(2)
Distance between (4,3) &(-4,3) is =√((4+4)² + (3-3)²)
= √(8)² 
= 8
As given in the question,
Equation (1) = (2)
(x-4)² = (x+4)² 
⇒ x² -8x+16 = x² +8x+16
⇒ 16x = 0
⇒ x = 0
Also, equation (1) = 8
(x-4)² +(y-3)² = 64  ...(3)
Putting the value of x in (3)
We get,
(0-4)² +(y-3)² = 64
⇒ (y-3)² = 64-16
⇒ (y-3)² = 48
⇒ y-3 = √48
⇒ y = 3 + 4√3, 3 - 4√3 
We do not take y = 3 + 4√3 as if y = 3 + 4√3 then origin cannot be at interior of triangle 
Therefore, the third vertex = (0, 3 - 4√3)

2. A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of △ ADE.

Solution

As given in the question, 
The three vertices of a parallelogram ABCD are A(6, 1), B(8, 2) and C(9, 4)
Let the fourth vertex of parallelogram = (x, y) 
We know that, diagonals of a parallelogram bisect each other 

Mid - point of a line segment joining the points (x₁ , y₁ ) and (x₂ , y₂ ) is given by, 

So, fourth vertex is D(7, 3)
Now, Midpoint of DC, 
(7 + 9)/2, (3 + 4)/2 = E 
⇒ 8, 7/2 = E 
Now,
Area of ΔABC with vertices (x₁ , y₁ ) and (x₂ , y₂ ) and (x₃ , y₂ ) = ½ [ x₁(y₂ – y₃ ) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂) ] 
Area of ΔADE with vertices A (6, 1), D(7, 3) and E(8, 7/2)
Putting value in the formula we get, 
The required area of ΔADE is 3/4 sq. units.

3. The points A (x₁ , y₁ ), B (x₂ , y₂ ) and C (x₃ , y₃ ) are the vertices of ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
(iv) What are the coordinates of the centroid of the triangle ABC?

Solution

Given, 
The vertices of ΔABC = A, B and C
Coordinates of A, B and C = A (x₁ , y₁ ), B (x₂ , y₂ ) , C (x₃ , y₃ )
(i) As given in the question D is the mid - point of BC and it bisect the line into two equal parts. 
Coordinates of the mid - point of BC; 
D = [(x₂ + x₃ )/2 , (y₂ + y₃ )/2]
(ii) Let the coordinates of a point P be (x, y) 

Given, 
The ratio in which the point P(x, y), divide the line joining, 
A (x₁ , y₁) and D = [(x₂ + x₃)/2 , (y₂ + y₃)/2] = 2 : 1 
Then, 
Coordinates of P = 

(iii) Let the coordinates of a point Q be (p, q) 

Given, 
The point Q (p, q), divides the line B and E in 2 : 1, 

Also, 
Midpoint of AC = Coordinates of E (As BE is median of CE), 
E = [ (x₁ , x₃ )/2 , (y₁ , y₃ )/2]
Also point R divides the line CF in the ratio 2 : 1, 
So coordinates of R = 

(iv) Coordinates of the centroid of the ΔABC, 
R = [(Sum of all coordinates of all vertices)/3, (Sum of all coordinates of all vertices)/3]
R = [(x₂ + x₃ + x₁ )/3, (y₂ + y₃ + y₁)/3]

4. If the points A (1, –2), B (2, 3) C (a, 2) and D (– 4, –3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base.

Solution
In parallelogram, we know that, diagonals are bisects each other so,
Mid-point of AC = mid-point of BD

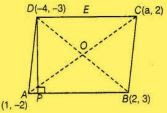
[(1 + a)/2 , (-2+2)/2] = [(2 - 4)/2, (3 - 3)/2]

⇒ (1 + a)/2 = -2/2 
⇒ a = -1
So, the required value of a is – 3.

Given that, AS as base of a parallelogram and drawn a perpendicular from D to AS which

meet AS at P. So, DP is a height of a parallelogram.

Equation of the points passing through the points (1,-2) and (2,3) is :

Taking slope of DP m₂ , as DP is perpendicular to AB, we can apply the condition, 
m₁ . m₂ = -1
⇒ 5.m₂ = -1
⇒ m₂ = -1/5
Now, equation of DP having slope m₂ , passing through point (-4, -3) is, 
y - y₁ = m₂ (x - x₁ )
⇒ y + 3 = (-1/5)(x + 4) 
⇒ x + 5y = -19
Now, on solving both the equations we ge, 
x = 8/13
y = -51/13
Coordinates of P = (8/13, -51/13)
So, height of parallelogram, 

5. Students of a school are standing in rows and columns in their playground for a drill practice. A, B, C and D are the positions of four students as shown in figure. Is it possible to place Jaspal in the drill in such a way that he is equidistant from each of the four students A, B, C and D?

If so, what should be his position?

Solution

Yes, from the figure we observe that the positions of four students A, B, C and D are (3, 5),

(7, 9), (11, 5) and (7,1) respectively and these are four vertices of a quadrilateral.

Now, we will find the type of this quadrilateral.

For this, we will find all its sides.

BD = 8 
As, 
AB = BC = CD = DA 
Also, AC = BD 
We see that, AB = BC = CD = DA, all sides are equal.

So, it represents a square.

Coordinates of point P = Mid point of AC 
[(3 + 11)/2, (5+5)/2]
(7, 5) 

The required position of Jaspal is (7, 5).

6. Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in km.   

Solution

In the figure we had located every place with its coordinates and direction, 
By distance formula, 
= √[(x₂ – x₁)² + (y₂ – y₁)²]
Distance between house and the bank =  √[(5 – 2)² + (8 – 4)²] = 5 
Distance between bank and the daughter school = √[(13 – 5)² + (14 – 8)²] = 10
Distance between the daughter school and office = √[(13 – 13)² - (26 – 14)²] = 12  
Now, 
Total distance = 5 + 10 + 12 = 27 units 

Now, 
Distance between house to offices = √[(13 – 2)² + (26 – 4)²] = 24.6 km

Therefore, extra distance travelled by Ayush in reaching his office;

= 27 – 24.6

= 2.4 km

Hence, the required extra distance travelled by Ayush is 2.4 km.