Chapter 2 Exponents of Real Numbers RD Sharma Solutions Exercise 2.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 2 Exponents of Real Numbers Exercise 2.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	No other Exercises
Related Study	NCERT Solutions for Class 10 Maths

Exercise 2.1 Solutions

1. Assuming that x, y, z are positive real numbers, simplify each of the following :
(i) (√(x^-3)⁵
(ii) √(x³y^-2 )
(iii) [x^-2/3 y^-1/2 ]²
(iv) (√x)^-2/3 (√y⁴) ÷ √(xy) ^-1/2
(v)
(vi) [x^-4/y^-10]^5/4

Solution

(i) We have,

(ii) We have,

(iii) We have,

(iv) We have,

(v) We have,

(vi) We have,

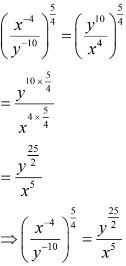
2. Simplify :
(i) [16^-1/5]^5/2(ii) ∛(342)^-2(iii) (0.001)^1/3(iv) [(25)^3/2 × (243)^3/5 ]/[(16)^5/4 × (8)^4/3 ]
(v) (√2/5)⁸ ÷ (√2/5)¹³
(vi) [(5^-1 × 7²)/(5² × 7^-4)]^7/2 × [(5^-2 × 7³ )/(5³ × 7^-5 )]^-5/2

Solution

3. Prove that :
(i) 9^3/2 – 3×5⁰ – (1/81)^-1/2 = 15
(ii) (1/4)^-2 – 3×8^2/3 × 4⁰ + (9/16)^-1/2 = 16/3
(iii) [2^1/2 × 3^1/3 × 4^1/4]/[10^-1/5 × 5^3/5 ] ÷ [3^4/3 × 5^-7/5 ]/[4^-3/5 × 6] = 10
(iv) [(0.6)⁰ – (0.1)^-1]/[(3/8)^-1 (3/2)³ + (-1/3)^-1 ] = -3/2
(v) √(1/4) + (0.01)^-1/2 – (27)^2/3 = 3/2
(vi) (2ⁿ + 2^n-1)/(2ⁿ⁺¹ – 2ⁿ ) = (2ⁿ + 2ⁿ × 2^-1)/(2ⁿ × 2¹ – 2ⁿ )
(vii) (64/125)^-2/3 + 1/(256/625)^1/4 + (√25/∛64)
(viii) (3^-3 × 6² × √98)/[5² × ∛1/25 × (15)^-4/3 × 3^1/3 ]

Solution