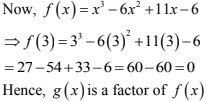Chapter 6 Factorisation of Algebraic Expressions RD Sharma Solutions Exercise 6.4 Class 9 Maths

Chapter Name | RD Sharma Chapter 6 Factorisation of Polynomials Exercise 6.4 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 6.4 Solutions
In each of the following, use factor theorem to find whether polynomial g(x) is a factor of polynomial f(x) or, not: (1 - 7)
1. f(x) = x3 - 6x2 + 11x - 6; g(x) = x - 3
Solution
We have f(x) = x3 - 6x2 + 11x - 6 and g(x) = x - 3
In order to find whether polynomial g(x) = x - 3 is a factor of f(x), it is sufficient to show that f(3) =0
Solution
We have
f(x) = 3x3 + 17x3 + 9x3 - 7x - 10; and g(x) = x + 5
In order to find whether g(x) = x - (-5) is a factor of f(x) or not, it is sufficient to show that f(-5) = 0
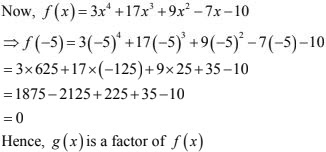
3. f(x) = x5 + 3x4 - x3 - 3x2 + 5x + 15, g(x) = x + 3
Solution
We have
f(x) = x5 + 3x4 - x3 - 3x2 + 5x + 15, and g(x) = x + 3
In order to find whether g(x) = x -(-3) is a factor of f(x) or not, it is sufficient to prove that f(-3) = 0


4. f(x) = x3 - 6x3 - 19x + 84, g(x) = x - 7
Solution
We have, f(x) = x3 - 6x3 - 19x + 84, and g(x) = x - 7
In order to find whether g(x) = x -7 is a factor of f(x) or not, it is sufficient to show that f(7) = 0

In order to find whether g(x) = x -7 is a factor of f(x) or not, it is sufficient to show that f(7) = 0

5. f(x) = 3x3 + x2 - 20x + 12 and g(x) = 3x - 2
Solution
We have
f(x) = 3x3 + x2 - 20x + 12 and g(x) = 3x - 2
In order to find whether g(x) = 3(x - 2/3) is a factor of f(x) or not, it is sufficient to prove
that f(2/3) = 0

6. f(x) = 2x3 - 9x2 + x + 12, g(x) = 3 - 2x
Solution
We have f(x) = 2x3 - 9x2 + x + 12, and g(x) = 3 - 2x
In order to find whether g(x) = 3 - 2x = -2(x - 3/2) is a factor of f(x) or not, it is sufficient to prove that f(3/2) = 0

7. f(x) = x3 - 6x2 + 11x - 6, g(x) = x3 - 3x + 2
Solution
We have
f(x) = x3 - 6x2 + 11x - 6, g(x) = x3 - 3x + 2
f(x) = x3 - 6x2 + 11x - 6, g(x) = x3 - 3x + 2
⇒ g(x) = x2 - 3x + 2 = (x - 1)(x - 2)
Clearly, (x - 1) and (x - 2) are factors of g(x)
In order to find whether g(x) = (x - 1)(x - 2) is a factor of f(x) or not, it is sufficient to prove that (x - 1) and (x - 2) are factors of f(x).
Clearly, (x - 1) and (x - 2) are factors of g(x)
In order to find whether g(x) = (x - 1)(x - 2) is a factor of f(x) or not, it is sufficient to prove that (x - 1) and (x - 2) are factors of f(x).
i.e., we should prove that f(1) = 0 and f(2) = 0

8. Show that (x - 2), (x + 3) and (x - 4) are factors of x3 - 3x2 - 10x + 24.
Solution
Let f(x) = x3 - 3x2 - 10x + 24 be the given polynomial.
In order to prove that (x - 2), (x + 3), (x - 4) are factors of f(x), it is sufficient to prove that f(2) = 0, f(-3) = 0 and f(4) = 0 respectively.
In order to prove that (x - 2), (x + 3), (x - 4) are factors of f(x), it is sufficient to prove that f(2) = 0, f(-3) = 0 and f(4) = 0 respectively.
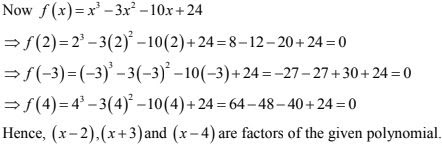
Solution
Let f(x) = x3 - 6x2 - 19 + 84 be the given polynomial
In order to prove that (x + 4), (x - 3) and (x - 7) are factors of f(x), it is sufficient to prove that f(-4) = 0 , f(3) = 0 and f(7) = 0 respectively

In order to prove that (x + 4), (x - 3) and (x - 7) are factors of f(x), it is sufficient to prove that f(-4) = 0 , f(3) = 0 and f(7) = 0 respectively

10. For what value of a is (x - 5) a factor of x3 - 3x3 + ax - 10 ?
Solution
Let f(x) = x3 - 3x3 + ax - 10 be the given polynomial
From factor theorem,
If (x - 5) is a factor of f(x) then f(5) = 0
From factor theorem,
If (x - 5) is a factor of f(x) then f(5) = 0

11. Find the value of a such that (x - 4) is a factor of 5x3 - 7x2 - ax - 28.
Solution
Let f(x) = 5x3 - 7x2 - ax - 28 be the given polynomial from factor theorem, if (x - 4) is a factor of f(x) then f(4) = 0

Hence (x - 4) is a factor of f(x) when a = 45
12. For what value of a, if x + 2 is a factor of factor of 4x4 + 2x3 - 3x2 + 8x + 5a.
Solution
Let f(x) = 4x4 + 2x3 - 3x2 + 8x + 5a be the given polynomial
From factor theorem if (x + 2) is a factor of f(x) then f(-2) = 0

From factor theorem if (x + 2) is a factor of f(x) then f(-2) = 0

Solution
Let f(x) = k2x3 - kx2 + 3kx - k be the given polynomial from factor theorem if (x - 3) is a factor of f(x) then f(3) = 0


14. Find the values of a and b, if x2 - 4 is a factor of ax4 + 2x3 - 3x2 + bx - 4.
Solution
Let f(x) = ax4 + 2x3 - 3x2 + bx - 4 and g(x) = x2 - 4
We have g(x) = x2 - 4 = (x - 2)(x + 2)
Given g(x) is a factor of f(x).
We have g(x) = x2 - 4 = (x - 2)(x + 2)
Given g(x) is a factor of f(x).

15. Find α and β, if x + 1 and x + 2 are factors of x3 + 3x2 - 2ax +β.
Solution
Let f(x) = x3 + 3x2 - 2ax +β be the given polynomial from factor theorem, if (x + 1) and (x + 2) are factors of f(x) then f(-1) = 0 and f(-2) = 0

16. Find the values of p and q so that x3 + px3 - 2x2 - 3x + q is divisible by (x2 - 1)
Solution
Let f(x) = x3 + px3 + 2x3 - 3x + q be the given polynomial and let g(x) = x3 - 1 = (x - 1)(x + 1)
Clearly, (x - 1) and (x + 1) are factors of g(x)
Given g(x) is a factor of f(x)
⇒ (x - 1) and (x + 1) are factors of f(x)
From factor theorem,
If (x - 1) and (X + 1) are factors of f(x) then f(1) = 0 and f-1) = 0 respectively
Clearly, (x - 1) and (x + 1) are factors of g(x)
Given g(x) is a factor of f(x)
⇒ (x - 1) and (x + 1) are factors of f(x)
From factor theorem,
If (x - 1) and (X + 1) are factors of f(x) then f(1) = 0 and f-1) = 0 respectively

17. Find the values of a and b so that (x + 1) and (x - 1) are factors of x4 + ax3 - 3x2 + 2x + b.
Solution
Let f(x) = x4 + ax3 - 3x2 + 2x + b be the given polynomial.
From factor theorem ; if (x + 1) and (x - 1) are factors of f(x) then f(-1) = 0 and f(1) = 0 respectively.
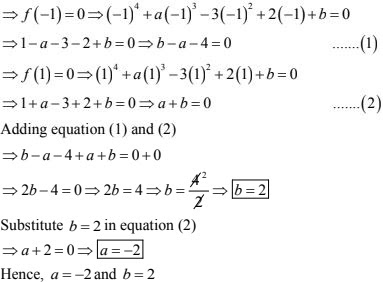
18. If x3 + ax2 - bx + 10 is divisible by x2 - 3x + 2, find the values of a and b.
Solution
Let f(x) = x3 + ax2 - bx + 10 and g(x) = x2 - 3x + 2 be the given polynomials.
We have g(x) = x2 - 3x + 2 = (x - 2)(x - 1)
⇒Clearly, (x - 1) and (x - 2) are factors of g(x)
Given that f(x), is divisible by g(x)
⇒ g(x) is a factor of f(x)
⇒ (x - 2) and (x - 1) are factors of f(x)
From factor theorem,
If (x - 1) and (x - 2) are factors of f(x) then f(1) = 0 and f(2) = 0 respectively.
Given that f(x), is divisible by g(x)
⇒ g(x) is a factor of f(x)
⇒ (x - 2) and (x - 1) are factors of f(x)
From factor theorem,
If (x - 1) and (x - 2) are factors of f(x) then f(1) = 0 and f(2) = 0 respectively.

19. If both x + 1 and x - 1 are factors of ax3 + x2 - 2x + b, find the values of a and b.
Solution
Let f(x) = ax3 + x2 - 2x + b be the given polynomial.
Given (x + 1) and (x - 1) are factor of f(x).
From factor theorem,
If (x + 1) and (x - 1) are factors of f(x) then f(-1) = 0 and f(1) = 0 respectively.
From factor theorem,
If (x + 1) and (x - 1) are factors of f(x) then f(-1) = 0 and f(1) = 0 respectively.

20. What must be added to x3 - 3x2 - 12x + 19 so that the result is exactly divisible by x2 + x - 6 ?
Solution
Let p(x) = x3 - 3x2 - 12x + 19 and q(x) = x2 + x - 6.
By division algorithm, when p(x) is divided by q(x), the remainder is a linear expression in x.
By division algorithm, when p(x) is divided by q(x), the remainder is a linear expression in x.
So, let r(x) = ax + b is added to p(x) so that p(x) + r(x) is divisible by q(x).
Let f(x) = p(x)+ r(x)

21. What must be subtracted from x3 - 6x2 - 15x + 80 so that the result is exactly divisible by x2 + x - 12 ?
Solution
Let p(x) = x3 - 6x2 - 15x + 80 and q(x) = x2 + x - 12
By division algorithm, when p(x) is divided nu q(x) the remainder is a linear expression in x.
So, let r(x) = ax + b is subtracted from p(x), So that p(x) - r(x) is divisible by q(x)
Let f(x) - p(x) - r(x)
Clearly, (3x - 2) and (x + 3) are factors of q(x)
Therefore, f(x) will be divisible by q(x) if (3x - 2) and (x + 3) are factors of f(x) i.e., from factor theorem,

By division algorithm, when p(x) is divided nu q(x) the remainder is a linear expression in x.
So, let r(x) = ax + b is subtracted from p(x), So that p(x) - r(x) is divisible by q(x)
Let f(x) - p(x) - r(x)
Clearly, (3x - 2) and (x + 3) are factors of q(x)
Therefore, f(x) will be divisible by q(x) if (3x - 2) and (x + 3) are factors of f(x) i.e., from factor theorem,

22. What must be added to 3x3 + x2 - 22x + 9 so that the result is exactly divisible by 3x3 + 7x - 6?
Solution
Let p(x) = 3x3 + x2 - 22x + 9 and q(x) = 3x3 + 7x - 6
By division algorithm,
When p(x) is divided by q(x), the remainder is a linear equation in x.
So, let r(x) = ax + b is added to p(x), so that p(x) + r(x) is divisible by q(x)
Let f(x) = p(x) + r(x)
When p(x) is divided by q(x), the remainder is a linear equation in x.
So, let r(x) = ax + b is added to p(x), so that p(x) + r(x) is divisible by q(x)
Let f(x) = p(x) + r(x)

23. If x - 2 is a factor of each of the following two polynomials, find the values of a in each case :
(i) x3 - 2ax2 + ax - 1
(ii) x5 - 3x4 - ax3 + 3ax2 + 2ax + 4
(ii) x5 - 3x4 - ax3 + 3ax2 + 2ax + 4
Solution

24. In each of the following two polynomials, find the value of a, if x - a is a factor:
(i) x6 - ax5 + x4 - ax3 + 3x - a + 2
(ii) x5 - a2x3 + 2x + a + 1
Solution(ii) x5 - a2x3 + 2x + a + 1
Let f(x) = x6 - ax5 + x4 - ax3 + 3x - a + 2 be the given polynomial.
From factor theorem,
If (x - a) is a factor of f(x) then f(a) = 0 [ ∵ x - a = 0 ⇒ x = a]

25. In each of the following two polynomials, find the value of a, if x + a is a factor.
(i) x3 + ax2 - 2x + a + 4
(ii) x4 - a2x2 + 3x - a
(i) x3 + ax2 - 2x + a + 4
(ii) x4 - a2x2 + 3x - a
Solution