Chapter 6 Factorisation of Algebraic Expressions RD Sharma Solutions Exercise 6.3 Class 9 Maths

Chapter Name | RD Sharma Chapter 6 Factorisation of Polynomials Exercise 6.3 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 6.3 Solutions
In each of the following, using the remainder theorem, find the remainder when f(x) is divided by g(x) and verify the result by actual division : (1 - 8)
1. f(x) = x3 + 4x2 - 3x + 10, g(x) = x + 4
Solution
We have f(x) = x3 + 4x2 - 3x + 10, g(x) = x + 4
Therefore, by remainder theorem when f(x) is divided by g(x) = x - (- 4), the remainder is equal to f(-4)
2. f(x) = 4x4 - 3x3 - 2x2 + x - 7, g(x) = x - 1
Solution
We have,
f(x) = 4x4 - 3x3 - 2x2 + x - 7, and g(x) = x - 1
Therefore by remainder theorem when f(x) is divide by g(x) = x - 1, the remainder is equal to f(+1)
Solution
We have,
f(x) = 2x4 - 6x3 + 2x2 - x + 2, and g(x) = x + 2
Therefore, by remainder theorem when f(x) is divide by g(x) = x - (-2), the remainder is equal to f(-2)


4. f(x) = 4x3 - 12x3 + 14x - 3, g(x) = 2x - 1
Solution
We have
f(x) = 4x3 - 12x3 + 14x - 3, and g(x) = 2x - 1
Therefore, by remainder theorem when f(x) is divide by g(x) = 2[x - 1/2], the remainder is equal to f(1/2)

f(x) = 4x3 - 12x3 + 14x - 3, and g(x) = 2x - 1
Therefore, by remainder theorem when f(x) is divide by g(x) = 2[x - 1/2], the remainder is equal to f(1/2)

5. f(x) = x3 - 6x3 + 2x - 4, g(x) = 1 - 2x
Solution
We have
f(x) = x3 - 6x3 + 2x - 4, and g(x) = 1 - 2x
Therefore, by remainder theorem when f(x) is divided by g(x) = -2(x - 1/2), the remainder is equal to f(1/2)
f(x) = x3 - 6x3 + 2x - 4, and g(x) = 1 - 2x
Therefore, by remainder theorem when f(x) is divided by g(x) = -2(x - 1/2), the remainder is equal to f(1/2)
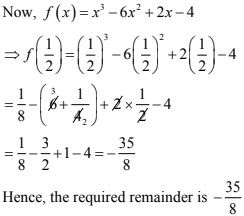
6. f(x) = x3 - 3x3 + 4, g(x) = x - 2
Solution
We have
f(x) = x3 - 3x3 + 4, and g(x) = x - 2
Therefore, by remainder theorem when f(x) is divided by g(x) = x - 2, the remainder is equal to f(2)


7. f(x) = 9x3 - 3x3 + x - 5, g(x) = x - 2/3
Solution
We have
f(x) = 9x3 - 3x3 + x - 5, and g(x) = x - 2/3
Therefore, by remainder theorem when f(x) is divided by g(x) = x - 2/3, the remainder is equal to f(2/3)

f(x) = 9x3 - 3x3 + x - 5, and g(x) = x - 2/3
Therefore, by remainder theorem when f(x) is divided by g(x) = x - 2/3, the remainder is equal to f(2/3)

8. f(x) = 3x3 + 2x3 - x3/3 - x/9 + 2/27, g(x) = x+ 2/3
Solution
We have,

9. If the polynomials 2x3 + ax2 + 3x - 5 and x3 + x2 -4x + a leave the same remainder when divided by x - 2, find the value of a.
Solution
Let p(x) = 2x3 + ax2 + 3x - 5 and q(x) = x3 + x2 - 4x + a be the given polynomials
The remainders when p(x) and q(x) are divided by (x - 2) are p(2) and q(2) respectively.
The remainders when p(x) and q(x) are divided by (x - 2) are p(2) and q(2) respectively.
By the given condition we have

10. The polynomials ax3 + 3x2 - 3 and 2x3 - 5x + a when divided by (x - 4) leave the remainder R1 and R2 respectively. Find the values of a in each of the following cases, if
(i) R1 = R2
(ii) R1 + R2 = 0
(iii) 2R1 + R2 = 0
Solution

11. If the polynomials ax3 + 3x2 - 13 and 2x3 - 5x + a, when divided by (x - 2) leave the same remainder, find the value of a.
Solution



