RD Sharma Solutions for Class 9 Chapter 5 Factorisation of Algebraic Expressions Exercise 5.1

Chapter 5 Factorisation of Algebraic Expressions RD Sharma Solutions Exercise 5.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 5 Factorisation of Algebraic Expressions Exercise 5.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 5.2 Exercise 5.3 Exercise 5.4
Related Study	NCERT Solutions for Class 10 Maths

Exercise 5.1 Solutions

Factorize : 

1. x³ + x – 3x² - 3

Solution

x³ + x – 3x² - 3
Taking x common in (x³ + x)
= x(x² + 1) - 3x² - 3 
Taking -3 common in (-3x² - 3)
= x(x² +1) - 3(x² + 1)
Now, we take (x² + 1) common 
= (x² + 1)(x - 3)
∴ x³ + x - 3x² - 3 = (x² + 1)(x - 3)

2. a(a + b)³ - 3a² b(a +b)

Solution

Taking (a + b) common in two terms 
= (a + b){a(a + b)² - 3a²b}
Now, using (a + b)² = a² + b² + 2ab

3. x(x³ - y³ ) + 3xy(x - y) 

Solution

4. a²x² + (ax² + 1)x + a

Solution

We multiply x(ax² + 1) = ax³ + x

5. x² + y - xy - x

Solution

On rearranging 
x² + y - xy - x 
Taking x common in the (x² + y) and -1 in (-x + y) 
= x( x - y)-1(x - y) 
Taking (x - y) common in both the terms 
= (x - y)(x - 1) 
∴ x² + y - xy - x = (x- y)(x - 1)

6. x³ - 2x²y + 3xy² - 6y³ 

Solution

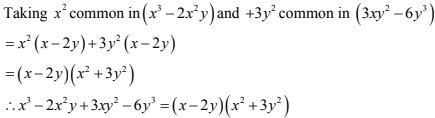
7. 6ab - b² + 12ac - 2bc

Solution

Taking common b in (6ab - b² ) and 2c in (12ac - 2bc)
= b(6a - b) + 2c(6a - b)
Taking (6a - b) common in both terms 
= (6a - b)(b + 2c) 
∴ 6ab - b² + 12ac - 2bc = (6a - b)(b + 2c)

8. [x² + 1/x² ] - 4[x + 1/x] + 6

Solution

9. x(x - 2)(x - 4) + 4x - 8

Solution

= x(x - 2)(x - 4) + 4(x - 2)
Taking (x - 2)common in both terms 
= (x - 2){x(x - 4)+ 4}
= (x - 2){x² - 4x + 4}
Now splitting middle term of x² - 4x + 4 

10. (x + 2)(x² + 25) - 10x² - 20x 

Solution

11. 2a² + 2√6ab + 3b² 

Solution

12. (a - b + c)² + (b - c + a)² + 2(a - b + c)(b - c + a)

Solution

Let (a - b + c) = x and (b - c + a) = y 

13. a² + b² 2(ab + bc + ca)

Solution

14. 4(x - y)² - 12(x - y)(x + y) + 9(x + y)² 

Solution

Let (x - y) = a, (x + y) = b 
= 4a² - 12ab + 9b² 
Splitting middle term -12 = -6 - 6 
also 4× 9 = -6 × - 6

15. a² - b² + 2bc - c² 

Solution

16. a² + 2ab + b² - c²

Solution

Using identity a² + 2ab + b² = (a + b)² 
= (a + b)² - c² 
Using identity a² - b² =(a +b)(a - b) 
= (a + b + c)(a + b - c)
∴ a² + 2ab + b² - c² = (a + b + c)(a + b -c)

17. a² + 4b² - 4ab - 4ac²

Solution

On rearranging 
= a² - 4ab + 4b² - 4c² 
= (a)² - 2× a × 2b + (2b)² - 4c² 
Using identity a² - 2ab + b² = (a - b)² 
= (a - 2b)² - 4c² 
= (a - 2b)² - 2c² 
Using identity a² - b² = (a + b)(a -b) 
= (a - 2b + 2c)(a - 2b - 2c)
∴ a² + 4b² - 4ab - 4c²  = (a - 2b +2c)(a - 2b - 2c)

18. xy⁹ - yx⁹ 

Solution

xy⁹ - yx⁹ 

19. x⁴ + x²y² + y⁴ 
Solution

Adding x² y² and subtracting x²y²  to the given equation 

20. x² - y² - 4xz + 4z² 

Solution

On rearranging the terms 

21. x² + 6√2 x + 10 

Solution

Splitting middle term, 

22. x² - 2√2x - 30

Solution

Splitting the middle term, 

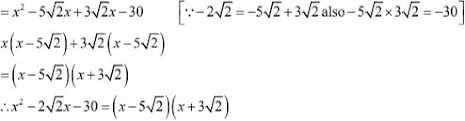
23. x²  - √3x - 6 

Solution

Splitting the middle term, 

24. x²  + 5√5x + 30 

Solution

Splitting the middle term, 

25. x²  + 2√3x - 24

Solution

Splitting the middle term, 

26. 2x²  - 5/6 x + 1/12

Solution

Splitting the middle term, 

27. x²  + 12/35 x + 1/35

Solution

Splitting the middle term, 

28. 21x²  - 2x + 1/21

Solution

29. 5√5x²  + 20x + 3√5

Solution

Splitting the middle term, 

30. 2x² + 3√5x + 5 

Solution

Splitting the middle term, 

31. 9(2a - b)²  - 4(2a - b) - 13 

Solution

Let 2a - b = x 

9x²  - 4x - 13 
Splitting the middle term, 

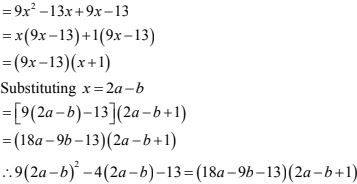
32. 7(x - 2y)² - 25(x - 2y) + 12

Solution

Let x - 2y = P
= 7P² - 25P + 12 
Splitting the middle term, 

= 7P² - 21P - 4P + 12 
= 7P (P - 3) -4(P - 3)
= (P - 3)(7P - 4) 
Substituting P = x - 2y 
= (x - 2y - 3){7(x - 2y) - 4)
= (x - 2y - 3)(7x - 14y - 4)
∴ 7(x - 2y)² - 25(x - 2y) + 12 = (x - 2y - 3)(7x - 14y - 4) 

33. 2(x + y)² - 9(x + y) - 5 

Solution

Let x + y = z 
= 2z²  - 9z - 5
Splitting the middle term, 

34. Given possible expressions for the length and breadth of the rectangle having 35y² + 13y - 12 as its area.

Solution

Area = 35y²  + 13y - 12 

Splitting the middle term, 
Area = 35y² + 28y - 15y - 12 
= 7y(5y + 4) - 3(5y + 4) 
Area = (5y + 4)(7y - 3)
Also area of rectangle  = Length × Breadth 
∴  Possible length = (5y + 4) and breadth = (7y - 3) 
Or Possible length = (7y - 3) and breadth = (5y + 4) 

35. What are the possible expressions for the dimensions of the cuboid whose volume is 3x² - 12x. 

Solution

Here volume = 3x²  - 12x 
= 3x(x - 4)
= 3× x(x-4)
Also volume = Length × Breadth × Height 
∴ Possible expressions for dimensions of the cuboid are = 3, x, (x - 4)