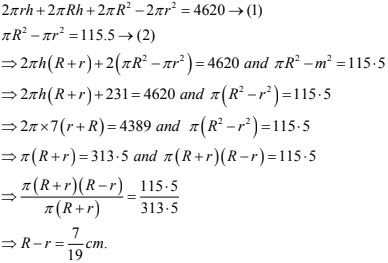RD Sharma Solutions for Class 9 Chapter 19 Surface Areas and Volume of a Circular Cylinder Exercise 19.1

Chapter 19 Surface Areas and Volume of a Circular Cylinder RD Sharma Solutions Exercise 19.1 Class 9 Maths

Chapter Name	RD Sharma Chapter 19 Surface Areas and Volume of a Circular Cylinder Exercise 19.1
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	No Other Exercises
Related Study	NCERT Solutions for Class 10 Maths

Exercise 19.1 Solutions

1. Curved surface area of a right circular cylinder is 4.4 m² . If the radius of the base of the cylinder is 0.7 m, find its height. 

Solution

Given that,
Radius of base of the cylinder e_r = 0.7 m
Curved surface area of cylinder = 4.4 m² = 2πrh
Let h be the height of the cylinder 
WKT,
2πrh = 4.4m² 
⇒ 2 ×3.14 ×0.7 ×h = 4.4
⇒ (4.4)h =  4.4 
⇒ h = 1 
∴ The height of the cylinder = 1m.

2. In a hot water heating system, there is a cylinder pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system. 

Solution

Given that 
Height of cylinder = length of cylinder pipe = 28 m.
Radius (r) of circular end of pipe = 5/2 cm = 2.5 cm = 0.025 m
Curved surface area of cylindrical pipe = 2πrh
= 2 × 3.14 ×0.025 ×28 = 4.4 cm 
∴ The area of radiation surface of the system is 4.4 m² or 44000cm²

3. A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of 12.50 per m²

Solution

Given that 
Height of the pillar = 3.5 m 
Radius of the circular end of the pillar = 50/2= cm. 
= 25 cm = 0.25 m 
Curved surface area of pillar = 2πrh

4. It is required to make a closed cylindrical tank of height 1 m and base diameter 1400 cm from a meal sheet. How many square meters of the sheet are required for the same ? 

Solution

Height of the cylindrical tank(h) = 1 m
Base radius of cylindrical tank (r) = 140/2 m = 70 cm = 0.7 m
Area of sheet required - total surface area of tank = 2π(r + h)
= 2 ×3.14 × 0.7 (0.7 + 1) m²
= 4.4 ×1.7 m²
= 7.48 m²
∴ So, it will required 7.48 m² of metal sheet.

5. A solid cylinder has total surface area of 462 cm² . Its curved surface area is one - third of its total surface area. Find the radius and height of the cylinder. 

Solution

We have 

6. The total surface area of a hollow cylinder which is open from both sides is 4620 sq. cm, area of base ring is 115.5 sq. cm and height 7 cm. Find the thickness of the cylinder.

Solution

Let the inner radii of hollow cylinder ⇒ r cm 
Outer radii of hollow cylinder ⇒ R cm 
Then, 

7. Find the ratio between the total surface area of a cylinder to its curved surface area, given that its height and radius are 7.5 cm and 3.5 cm.

Solution

For cylinder, total surface Area = 2πr(h + r)
Curved surface area = 2πrh 

8. The total surface area of a hollow metal cylinder, open at both ends of external radius 8 cm and height 10 cm is 338 p cm². Taking r to be inner radius, obtain an equation in r and use it to obtain the thickness of the metal in the cylinder.

Solution

Given that, 

External radius (R) = 8 cm
Height (h) = 10 cm 
The total surface area of a hollow metal cylinder = 338 IT cm²  
We know that 

9. A cylindrical vessel, without lid, has to be tin - coated on its both sides. If the radius of the base is 70 cm and height is 1.4 m, calculate the cost of tin - coating at the rate of Rs. 3.50 per 1000 cm² .

Solution

Given that 

r = 70 cm , h = 1.4m = 140 cm 

∴ Area to be tin coated  = 2(2πrh + πr² ) = 2πr(2h + r)
= 2 × 22/7 × 70(280 + 70) 
= 154000 cm² 
Required cost = (154000 × 3.50)/1000 = Rs. 539

10. The inner diameter of a circular well is 3.5 m. It is 10 m deep find.
(i) inner curved surface area.
(ii) the cost of plastering this curved surface at the rate of Rs. 40 per m²

Solution

Inner radius(r) of circular well = 1.75 m 
Depth (n) of circular well = 10 m

(i) Inner curved surface area = 2πrh
= 2 × 22/7 × 1.75 × 10m²
= (144 × 0.25 ×10)m²
= 110 m²

(ii) Cost of plastering 1m² area = Rs. 40
Cost of plastering 110 m² area = Rs.(110 × 40)= Rs. 4400

11. Find the lateral curved surface area of a cylinderical petrol storage tank that is 4.2 m in diameter and 4.5 m high. How much steel was actually used, if 1/12 of steel actually used was wasted in making the closed tank ?

Solution

Height (h) cylindrical tank = 4.5 m

Radius (r)  of circular end of cylindrical tank = 4.2/2 m = 2.1 m

(i) Lateral or curved surface area of tank = 2πrh
⇒ 2 × 3.14 × 2.1 ×4.5 m²
= 59.4 m²

(ii) Total surface area of tank = 2πr(r + h)

15. The students of a Vidyalaya were asked to participate in a competition for making and decorating pen holders in the shape of a cylinder with a base, using cardboard. Each pen holder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Solution

Radius of circular end of cylinder pen holder = 3 cm 

Height of pen holder = 10.5 cm 

Surface area of 1 pen holder = CSA of penholder + Area of base of SA of 1 penholder = 

Area of car board sheet used by 1 competitor = 1584/7 cm²
Area of car board sheet used by 35 competitors = 1584/7 × 35 cm² = 7920 cm²

13. The diameter of roller 1.5 m long is 84 cm. If it takes 100 revolutions to level a playground, find the cost of levelling this ground at the rate of 50 paise per square metre.

Solution

Given that, 

Diameter of the roller = 84 cm = 0.84m

Length of the roller = 1.5 m
Radius of the roller = D/2 = 0.84/2 = 0.42
Area covered by the roller on one revolution = covered surface area of roller 

Curved surface of roller = 2πrh = 2 × 22/7 × 0.42 × 1.5 = 0.12 ×22 × 1.5 m² 
Area of the playground = 100 × Area covered by roller in one revolution 
= (100 × 0.12 × 22 × 1.5)m² = 396 m² 
Now,
Cost of leveling 1m² = 50P = 50/100

⇒ P = 1/2
Cost of leveling 396 m²  = 1/2 × 396 = Rs. 198
Hence, cost of leveling 396 m² is Rs. 198

14. Twenty cylindrical pillars of the Parliament House are to be cleaned. If the diameter of

each pillar is 0.50 m and height is 4 m. What will be the cost of cleaning them at the rate of

Rs. 2.50 per square metre?

Solution

Diameter of each pillar = 0.5 m
Radius of each pillar (r) = a/2 = 0.5/2 = 0.25 m. 
Height of each pillar = 4m
Curved surface area of each pillar = 2πrh 
= 2 × 3.14 × 0.25 × 4m² 
= 44/7 m² 
Curved surface area of 20 pillars = 20 × 44/7 m² 
Given , cost of cleaning = Rs. 2.50 per square meter 

∴ Cost of cleaning 20 pillars = Rs. 2.50 × 20 ×44/7 = Rs. 314.28