Chapter 17 Constructions RD Sharma Solutions Exercise 17.3 Class 9 Maths

Chapter Name | RD Sharma Chapter 17 Constructions Exercise 17.3 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 17.3 Solutions
1. Construct a ΔABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B = 60°
Solution

Steps of construction :
- Draw a line segment BC of 3.6 cm.
- At the point B, draw ∠x BC of 60°
- With center B and radius 4.8 cm, draw an arc which intersects XB at D.
- Join DC
- Draw the perpendicular bisector of DC which intersects DB at A.
- Join AC
Hence ΔABC is the required triangle
2. Construct a ΔABC in which AB + AC = 5.6 cm, BC = 4.5 cm, AB - AC = 1.5 cm and ∠B = 45° .
Solution

Steps of construction :
- Draw a line segment BC of 4.5 cm.
- At B, draw an angle XBC of 45°
- With center B and radius 5.6 cm, draw an arc which intersects BX at D.
- Join DC
- Draw the perpendicular bisector of DC which intersects BD at A.
- Join AC
∴ Δ ABC is a required triangle
3. Construct a ΔABC in which BC = 3.4 cm, AB - AC = 1.5 cm and ∠B = 45°
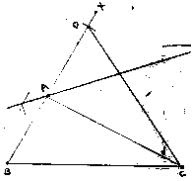 Steps of construction :
Steps of construction :
Solution

Steps of construction :
Step 1: Draw a line segment BC of 3.5 cm.
Step 2: At B, draw an angle XBC of 45°.
Step 3: With center B and radius 1.5 cm, draw an arc which intersects BX at D.
Step 4: Join DC
Step 5: Draw the perpendicular bisector of DC which intersects BD produced at A.
Step 6: Join AC
∴ ΔABC is the required triangle
4. Using ruler and compasses only construction a ΔABC, given base BC = 7cm, ∠ABC = 60° and AB + AC = 12 cm.
Solution

- Draw a line segment BC of 7 cm.
- At B, draw an angle XBC of 60°
- With center B and radius 12 cm, draw an arc which intersects BX at D.
- Join DC
- Draw the perpendicular bisector of DC which intersects BD at A.
- Join AC
∴ ΔABC is the required triangle.
5. Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45°.
Solution

Steps of construction :
- Draw a line segment XY of 6.4 cm.
- Draw ∠DXY = B = 60° and ∠EYX = ∠C = 45°
- Draw the angle bisector of ∠DXY and ∠EYX which interest each other at A.
- Draw the perpendicular bisector of AX and AY which interest XY at B and C respectively.
- Join AB and AC
∴ ΔABC is the required triangle.
6. Using ruler and compasses only, construct a ΔABC from the following data :
AB + BC + CA = 12 cm, ∠B = 45° and ∠C = 60° .
Solution

Steps of construction :
Step 1: Draw a line segment XY of 12 cm.
Step 2: Draw ∠DXY = ∠B = 45° and ∠EYX = ∠C = 60°
Step 3: Draw the angle bisectors of angles of DXY and EYX which intersects each other at A.
Step 4: Draw the perpendicular of AX and AY which intersect XY at B and C respectively.
Step 5: Join AB and AC
∴ ΔABC is the required triangle .
7. Construct a right - angled triangle whose perimeter is equal to 10 cm and one acute angle to 60°.
Solution

Steps of construction :
Step 1: Draw a line segment XY of 10 cm.
Step 2: Draw ∠DXY = ∠B = 90° and ∠FYX = ∠C = 60°
Step 3: Draw the angle bisectors of ∠DXY and ∠EYX which intersects each other at A. Step 4: Draw the perpendicular of AX and AY which intersect XY at B and C respectively.
Step 5: Join AB and AC
∴ ΔABC is the required triangle
8. Construct a triangle ABC such that BC= 6 cm, AB = 6cm and median AD = 4 cm.
Solution

Steps of construction :
Step 1: Draw a line segment BC of 6 cm.
Step 2: Take midpoint D of BC.
Step 3: With center B and D and radii 6 cm and 4 cm draw two arcs which intersects each other A.
Step 4: Join AB, AD and AC
∴ Δ ABC is the required triangle
9. Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Solution

Steps of construction :
Step 1: Draw a line segment BC of 6cm.
Step 2: At B draw an angle le × BC of 90° .
Step 3: With center B and radius 10cm draw an arc which intersects XB at D.
Step 4: Join DC. Step 5: Draw the perpendicular bisector of DC which intersects DB at A
Step 6: Join AC
∴ ΔABC is the required triangle
10. Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11.

Solution

Steps of construction :
Step 1: Draw a line segment AB of 11 cm.
Step 2: Draw ∠DAB = Y = 30° and ∠FBA = ∠Z = 90°
Step 3: Draw the angle bisector of ∠DAB and ∠EBA which intersect each other at x
Step 4: Draw the perpendicular bisector XA and XB which intersect AB at Y and Z respectively.
Step 5: Join XY and XZ
∴ ΔXYZ is the required triangle .
