Chapter 16 Circles RD Sharma Solutions Exercise 16.2 Class 9 Maths

Chapter Name | RD Sharma Chapter 16 Circles Exercise 16.2 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 16.2 Solutions
1. The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.
Solution
Given that,
Radius of circles (OA) = 8 cm
Chord (AB) = 12 cm
Draw OC ⊥ AB.
WKT,
The perpendicular from center to chord bisects the chord
∴ AC = BC = 12/2 = 6 cm
Now in ΔOCA, by Pythagoras theorem
2. Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm.
Solution

Given that
Distance (OC) = 5 cm
Radius of circle (OA) = 10 cm
In ΔOCA by Pythagoras theorem

3. Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Solution

AC = BC = 4.47 cm
Then, AB = 4.47 + 4.47 = 8.94 cm .
4. Two chords AB, CD of length 5 cm, 11 cm respectively of a circle are parallel. If the distance between AB and CD is 3cm, find the radius of the circle.
Solution

5. Give a method to find the centre of a given circle.
Solution
Steps of construction:
(1) Take three point A, B and C on the given circle
(2) Join AB and BC
(3) Draw thee perpendicular bisectors of chord AB and BC which intersect each other at O
(4) Point will be required circle because WKT, perpendicular bisector of chord always passes through center

6. Prove that the line joining the mid - point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Solution
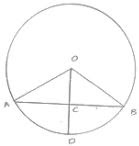
Given : C is the midpoint of chord AB
To prove : D is the midpoint of arc AB
Proof:
In ΔOAC and ΔOBC
OA = OB [Radius of circle]
OC = OC [Common]
AC = BC [C is the midpoint of AB]
Then, ΔOAC ≅ ΔOBC [By SSS condition ]
∴ ∠AOC = ∠BOC [c.p.c.t]

OC = OC [Common]
AC = BC [C is the midpoint of AB]
Then, ΔOAC ≅ ΔOBC [By SSS condition ]
∴ ∠AOC = ∠BOC [c.p.c.t]

7. Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Solution

Given : PQ is a diameter of circle which Bisects
Chord AB at C
To prove : PQ bisects ∠AOB
Proof:
In ΔAOC and ΔBOC
OA = OB [Radius of circle]
OC = OC [Common]
AC = BC [Given]
Then ΔAOC ≅ ΔBOC [by SSS condition]
∴ ∠AOC = ∠BOC [c.p.c.t]
OC = OC [Common]
AC = BC [Given]
Then ΔAOC ≅ ΔBOC [by SSS condition]
∴ ∠AOC = ∠BOC [c.p.c.t]
Hence PQ bisects ∠AOB
8. Given an arc of a circle, show how to complete the circle.
Solution

Steps of construction :
(i) Take three point A, B and C on the given Arc
(ii) Join AB and BC
(iii) Draw the perpendicular bisectors of chords AB and BC which interest each other at point O, then O will required center of the required circle
(iv) Join OA
(v) With center O and radius OA, complete the circle
9. Prove that two different circles cannot intersect each other at more than two points.
Solution
Suppose two circles intersect in three points A,B,C,
Then A,B,C are non-collinear. So, a unique circle passes through these three points. This is
contradiction to the face that two given circles are passing through A,B,C. Hence, two
circles cannot intersect each other at more than two points.
10. A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
Solution

(i) Draw a line segment AB of 5cm
(ii) Draw the perpendicular bisectors of AB
(iii) Draw an arc which intersects the perpendicular bisectors at point O will be required
center.
(iv) With center O and radius OA draw a circle. No, we cannot draw a circle of radius
2cm passing through A and B because when we draw an arc of radius 2cm with
center A, the arc will not interest the perpendicular bisector and we will not find the
center
11. An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
Solution

Let ABC be an equilateral triangle of side 9 cm and let AD one of its medians. Let G be the centroid of ΔABC. Then AG : GD = 2 : 1
WKT in an equilateral centroid coincides with the circumcenter
Therefore, G is the center of the circumference with circum radius
GA
Also G is the center and GD ⊥ BC . Therefore,
In right triangle ADB, we have

12. Given an arc of a circle, complete the circle.
Solution
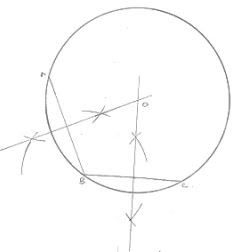
Steps of construction:
(i) Take three point A, B, C on the given Arc
(ii) Join AB and BC
(iii) Draw the perpendicular bisectors of chords AB and BC which interest each other at
point O, then O will required center of the required circle
(iv) Join OA
(v) With center O and radius OA, complete the circle
13. Draw different pairs of circles. How many points does each pair have in common ? What is the maximum number of common points ?
Solution

Each pair of circles have 0, 1, or 2 points in common
The maximum number of points in common is '2'
14. Suppose you are given a circle. Give a construction to find its centre.
Solution

Steps of constructions:
(1) Take three point A, B and C the given circle
(2) Join AB and BC
(3) Draw the perpendicular bisectors of chord AB and BC which intersect each other at O.
(4) Point O will be the required center of the circle because we know that the perpendicular
bisector of the cord always passes through the center
15. Two chords AB and CD of length 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
Solution
Draw OM ⊥ AB and ON ⊥ CD. Join OB and OD
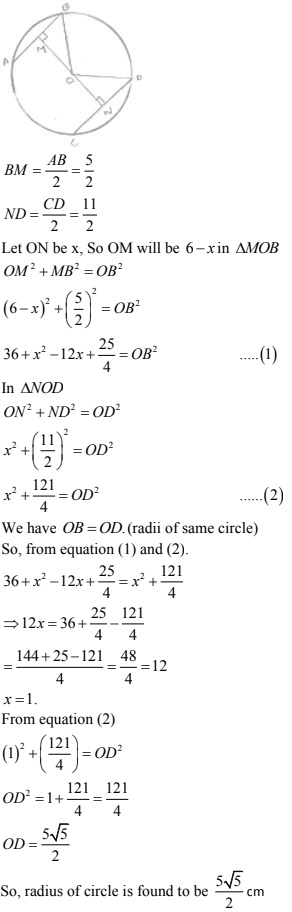
16. The lengths of two parallel chords of a circle are 6 cm and 8 cm if the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre ?
Solution

Distance of smaller chord AB from centre of circle = 4 cm , OM = 4 cm


