Chapter 13 Linear Equations in Two Variables RD Sharma Solutions Exercise 13.4 Class 9 Maths

Chapter Name | RD Sharma Chapter 13 Linear Equations in Two Variables Exercise 13.4 |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 13.4 Solutions
1. Given the geometric representations of the following equations
(a) on the number line
(b) on the Cartesian plane :
(i) x = 2
(ii) y + 3 = 0
(iii) y = 3
(iv) 2x+ 9 = 0
(v) 3x - 5 = 0
Solution

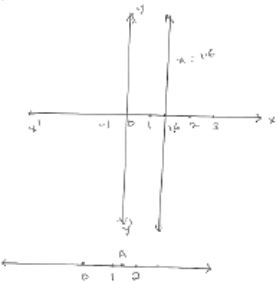
Point A represents x = 2 number line
On Cartesian plane, equation represents all points on y - axis for which x = 2
(ii)

y = 3
Point A represents 3 on number line

y = 3
Point A represents 3 on number line
On Cartesian plane, equation represents all the points on x - axis for which y = -3 .
(iii)

y = 3.
Point A represents 3 on number line
On Cartesian plane, equation represents all points all points on x - axis for which y = 3

2x + 9 = 0
2x = -9
x = -9/2 = -4.5
Point A represents -4.5 on number line
2x = -9
x = -9/2 = -4.5
Point A represents -4.5 on number line
On Cartesian plane, equation represents all points on y - axis for which x = -4.5
(v)
3x = 5
x = 5/3 = 1.6 (Approx)
Point A represents 1(1/2) or 5/3 on number line
On Cartesian plane, equation represents all points on y - axis for which x = 16
2. Give the geometrical representation of 2x + 13 = 0 as an equation in
(i) one variable
(i) one variable
(ii) two variable
Solution
Solution
(i)


One variable representation of 2x + 13 = 0
2x = -13
x = -13/2 = -6(1/2)
Points A represents -13/2
2x = -13
x = -13/2 = -6(1/2)
Points A represents -13/2
(ii)
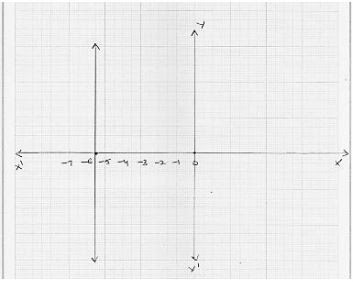
2x + 0y + 13 = 0
⇒ 2x + 13 = 0
⇒ 2x = - 13
⇒ x = -13/2
⇒ x = -6.5
On Cartesian plane, equation represents all points y - axis for which x = -6.5.
3. Solve the equation 3x + 2 = x - 8, and represent the solution (i) the number line (ii) the Cartesian plane.
Solution
(i)

⇒ 3x - x = -8 - 2
⇒ 2x = -10
⇒ x = -5
Points A represents -5 on number line

4. Write the equation of the line that is parallel to x - axis and passing through the point
(i) (0, 3)
(ii) (0, -4)
(iii) (2, -5)
(iv) (-4, - 3)
Solution
Solution
(i) The equation of the line that is parallel to x - axis and passing through the point (0, 3) is y = 3
(ii) The equation of the line that is parallel to x - axis and passing through the point (0, -4) is y = 4
(iii) The equation of the line that is parallel to x - axis and passing through the point (2, -5) is y = -5
(iv) The equation of the line that is parallel to x - axis and passing through the point (-4, - 3) is y = -3
(ii) The equation of the line that is parallel to x - axis and passing through the point (0, -4) is y = 4
(iii) The equation of the line that is parallel to x - axis and passing through the point (2, -5) is y = -5
(iv) The equation of the line that is parallel to x - axis and passing through the point (-4, - 3) is y = -3
5. Write the equation of the line that is parallel to y - axis and passing through the point
(i) (4, 0)
(ii) (-2, 0)
(iii) (3, 5)
(iv) (-4, -3)
Solution
(i) The equation of the line that is parallel to y - axis and passing through (4, 0) will be x = 4
(ii) The equation of the line that is parallel to y - axis and passing through (-2, 0) will be x = -2
(iii) The equation of the line that is parallel to y - axis and passing through (3, 5) will be x = 3
(iv) The equation of the line that is parallel to y- axis and passing through (-4, -3) will be x = -4.
(ii) The equation of the line that is parallel to y - axis and passing through (-2, 0) will be x = -2
(iii) The equation of the line that is parallel to y - axis and passing through (3, 5) will be x = 3
(iv) The equation of the line that is parallel to y- axis and passing through (-4, -3) will be x = -4.
