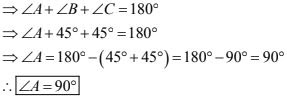RD Sharma Solutions for Class 9 Chapter 10 Congruent Triangles Exercise 10.6

Chapter 10 Congruent Triangles RD Sharma Solutions Exercise 10.6 Class 9 Maths

Chapter Name	RD Sharma Chapter 10 Congruent Triangles Exercise 10.6
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 10.1 Exercise 10.2 Exercise 10.3 Exercise 10.4 Exercise 10.5
Related Study	NCERT Solutions for Class 10 Maths

Exercise 10.6 Solutions

1. In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle. 

Solution

Given that in ΔABC, ∠A = 40° and ∠B = 60°

We have to find longest and shortest side 

We know that, 

Sum of angles in a triangle 180° 

2. In a ΔABC, if ∠B = ∠C = 45° , which is the longest side ?

Solution

Given that in ΔABC, 
∠B = ∠C = 45°
We have to find longest side 
We know that, 
Sum of angles in a triangle = 180°

3. In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60°, ∠A = 70° , prove that :

(i) AD > CD

(ii) AD > AC

Solution

Given that in ΔABC, side AB is produced to D So that BD = BC and ∠B = 60°, ∠A = 70°

We have to prove that 

(i) AD > CD 
(ii) AD > AC
First join C and D

Now, in ΔABC 

4. Is it possible to draw a triangle with sides of length 2cm, 3cm and 7cm ? 

Solution

Given length of sides are 2cm, 3cm and 7cm we have to check whether it is possible to draw a triangle with ten the given lengths of sides 

We know that, 

A triangle can be drawn only when the sum of any two sides is greater than the third side. 

So, let's check the rule. 

2 + 3 ⊁ 7 or 2 + 3 < 7
2 + 7 > 3
and 3 + 7 > 2
Here,  2 + 3 ⊁ 7 So, the triangle does not exit. 

5. O is any point in the interior of ΔABC. Prove that 

(i) AB + AC > OB + OC

(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC > 1/2(AB + BC + CA)

Solution

Given that O is any point in the interior of ΔABC 
We have to prove 

(i) AB + AC > OB + OC

(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC > 1/2(AB + BC + CA)

We know that, in a triangle the sum of any two sides is greater than the third side

So, we have 

In ΔABC 
AB + BC > AC

BC + AC > AB

AC + AB > BC

In ΔOBC 

OB + OC > BC ...(1)
In ΔOAC 

OA + OC > AC ...(2)
In ΔOAB

OA + OB > AB  ...(3)
Now, extend (or) produce BO to meet AC in D. 

Now, in ΔABD, we have 

AB + AD > BD 

⇒ AB + AD > BO + OD  ...(4) [∵ BD = BO + OD]

Similarly in ΔODC, we have 

OD + DC > OC ...(5)

6. Prove that the perimeter of a triangle is greater than the sum of its altitudes. 

Solution

Given A ΔABC in which AD ⊥ BC, BE ⊥ AC and CF ⊥ AB.

To prove : 

AD + BE + CF < AB + BC + AC

Figure : 

Proof: 

We know that of all the segments that can be drawn to a given line, from a point not lying on it, the perpendicular distance i.e., the perpendicular line segment is the shortest. 

Therefore,

AD ⊥ BC 

7. In Fig. 10.131, prove that : 

(i) CD + DA + AB + BC >2AC 
(ii) CD + DA + AB > BC 

Solution

Given to prove 

(i) CD + DA + AB + BC > 2AC 
(ii) CD + DA + AB > BC 

From the given figure, 

We know that, in a triangle sum of any two sides is greater than the third side.

(i) So, 

In ΔABC, we have 

AB + BC > AC    .....(1) 

8. Which of the following statement are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one. 

Solution

(i) False (F)
Reason: Sum of these sides of a triangle is greater than sum of its three altitudes

(ii) True (F)

(iii) True (T)

(iv) False (F)
Reason: The difference of any two sides of a triangle is less than third side.

(v) True (T)
Reason: The side opposite to greater angle is longer and smaller angle is shorter in a triangle

(vi) True (T)
Reason: The perpendicular distance is the shortest distance from a point to a line not containing it. 

9. Fill in the blanks to make the following statements true. 
(i) In a right triangle the hypotenuse is the ...... side.
(ii) The sum of three altitudes of a triangle is ..... than its perimeter.
(iii) The sum of any two sides of a triangle is .... than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the side opposite to it.
(v) Difference of any two sides of a triangle is than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.

Solution

(i) In a right triangle the hypotenuse is the largest side.
Reason : Since a triangle can have only one right angle, other two angles must be less than 90°.
⇒ The right angle is the largest angle.
⇒ Hypotenuse is the largest side. 
(ii) The sum of three altitudes of a triangle is less than its perimeter.
(iii) The sum of any two sides of a triangle is greater than the third side.
(iv) If two angles of a triangle are unequal, then the smaller angle has the smaller side opposite to it.
(v) Difference of any two sides of a triangle is less than the third side.
(vi) If two sides of a triangle are unequal, then the larger side has greater angle opposite to it.