RD Sharma Solutions for Class 10 Chapter 9 Arithmetic Progression Exercise 9.5

RD Sharma Solutions Chapter 9 Arithmetic Progression Exercise 9.5 Class 10 Maths

Chapter Name	RD Sharma Chapter 9 Arithmetic Progression
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 9.1 Exercise 9.2 Exercise 9.3 Exercise 9.4 MCQ
Related Study	NCERT Solutions for Class 10 Maths

Exercise 9.5 Solutions

1. Find the sum of the following arithmetic progressions: 
(i) 50, 46, 42, ...... to 10 terms 
(ii) 1, 3, 5, 7, ..... to  12 terms 
(iii) 3, 9/2, 6, 15/2, ..... to  25 terms 
(iv) 41, 36, 31, ..... to 12 terms 
(v) (a + b), (a - b), (a - 3b), ..... to 22 terms 
(vi ) (x - y)² ,(x² + y² ), (x + y)² ,......., to n terms 
(vii) (x - y)/(x + y), (3x - 2y)/(x + y), (5x - 3y)/(x + y), .... to n terms 
(viii) - 26, -24, -22, ..... to 36 terms 

Solution

In an A.P
Let,
First term = a, 
Common difference = d, and there are n terms. Then, sum of n terms is, 

2. Find the sum to n term of the A.P. 5, 2, - 1, -4, -7,..........

Solution

Given AP is 5, 2, -1, -4, -7,..........

3. Find the sum of n terms of an A.P. whose the terms is given by a_n = 5 – 6n.

Solution

4. If the sum of a certain number of terms starting from first term of an A.P. is 25, 22, 19, .... is 116. Find the last term.

Solution
Given AP is  25, 22, 19, ..... 
First term (a) = 25, d = 22 - 25 = -3. 
Given, S_n = n/2(2a + (n - 1)d)
116 = n/2(2×25+(n -1)-3)
⇒ 232 = n(50 - 3(n -1))
⇒ 232 = n(53 - 3n)
⇒ 232 = 53n - 3n² 
⇒ 3n² - 53n + 232 = 0 
⇒ (3n - 29)(n - 8) = 0 
∴ n = 8
⇒ a₈ = 25 + (8 - 1) - 3 
25 - 24 = 4
∴ n =8, a₈ = 4 

5. (i) How many terms of the sequence 18, 16, 14, .......... should be taken so that their 
(ii) How many terms are there in the A.P. whose first and fifth terms are -14  and 2 respectively and the sum of the terms is 40?
(iii) How many terms of the A.P. 9, 17, 25, ..... must be taken so that their sum is 636 ? 
(iv) How many terms of the A.P. 63, 60, 57, ...... must be taken so that their sum is 693 ? 

Solution

(i) Given sequence, 18, 16, 14, .....
a = 18, d = 16- 19 = - 2. 
Let, sum of n terms in the sequence is zero 

(ii) ∵ n = 0 is not possible. Therefore, sum of 19 number in the sequence is zero. 
Given, a = - 14, a₅ = 2
a + (5 - 1)d = 2 
⇒ -14 + 4d = 2 
⇒ 4d = 2+ 14 = 16 
⇒ d = 16/4 = 4 
Sequence is -14, -10, -6, -2, 2, .........

6. The first and the last terms of an A.P are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum ? 

Solution

Given, a = 17, L = 350, d = 9 
L = a_n  = a + (n - 1)d 
350 = 17 + (n - 1)9 
⇒ 333 = (n - 1)9
⇒ n - 1 = 333/9 = 37
⇒ n = 38
∴ 38 terms are there 
s_n  = n/2(a + l) 
= 38/2(17 + 350)
= 19.367 
∴ s_n  = 6973

7. The third term of an A.P is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference and the sum of first 20 terms. 

Solution

8. The first term of an A.P. is 2 and the last term is 50. The sum of all these terms is 442. Find the common difference. 

Solution

9. If  12 th term of an A.P. is  -13 and the sum of the first four terms is 24,  what is the sum of first 10 terms ? 

Solution

10. Find the sum of first 22 terms of an A.P. in which d = 22 and a = 149. 

Solution

11. Find the sum of all natural numbers between 1 and 100, which are divisible by 3. 

Solution

The numbers between 1 and  100 which are divisible by 3 are 3, 6, 9, ...  99. 
∴ Sum of all natural numbers between 1 and 100, which are divisible by 3 is 1683.

12. Find the sum of first n odd natural numbers. 

Solution

The sequence is 1, 3, 5, ......, n. 
In this first term (a) = 1, common difference d = 3 - 1 = 2 

13. Find the sum of all odd numbers between (i) 0 and 50  (ii) 100 and 200

Solution

(i) Odd numbers between 0 and 50 are 1, 3, 5, ...., 49 
In this a  = 1, d = 2, l = 49 = a_n  
49 = 1 + (n - 1)2  (∴ a_n  = a + (n - 1)d)

∴ Sum of all odd numbers between 0 and 50 is 625.

(ii) Odd numbers between 100 and 200 are 101, 103, ..... 199
In this a = 101, d = 2, l = a_n  = 199
199 = 101 + (n - 1)2
⇒ n - 1 = 98/2 = 49 
⇒ n = 49+ 1 = 50 
∴ There are 50 terms. 

14. Show that the sum of all odd integers between 1 and 1000 which are divisible by 3 is 83667. 

Solution

Odd integers between 1 and 1000 which are divisible by 3 are 3, 6, 9, 15, ....., 999. 

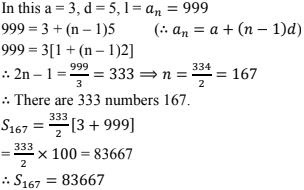
∴ Sum of all odd integers between 1 and 4000 which are divisible by 3 is 83667.

15. Find the sum of all integers between 84 and  719, which are muliples of 5. 

Solution

The numbers between 84 and 719, which are multiples of 5 are 85, 90, 95, ......, 715. 

∴ Sum of all integers between 84 and 719, which are multiples of 5 is 50800.

16. Find the sum of all integers between 50 and 500, which are divisible by 7. 

Solution

Numbers between 50 and 500, which are divisible by  7 are 56, 63, ......, 497.

∴ Sum of all integers between 50 and 500, which are divisible by 7 is 17696. 

17. Find the sum of all even integers between 101, and 999. 

Solution

Even integers between 101 and 999 are  102, 104, ....., 998

∴ Sum of all even integers between 101 and  999 is 24690. 

18. Find the sum of all integers between 100 and 550, which are divisible by 9. 

Solution

Integers between 100 and 550 which are divisible by 9 are  108, 117, .....,549.

∴ Sum of all integers between 100 and 550, which are divisible by 9 is 16425.

19. In an A.P., if the first term is 22, the common difference is - 4 and the sum to n terms is 64, find n. 

Solution

20. In an A.P., if the 5 the and 12th terms are 30 and 65 respectively, what is the sum of first 20 terms ? 

Solution

21.  Find the sum of the first 
(i) 11 terms of the A.P. 2, 6, 10, 14, .... 
(ii) 13 terms of the A.P.  -6, 0, 6, 12, ......
(iii) 51 terms of the A.P. whose second term is  2 and fourth term is 8. 

Solution

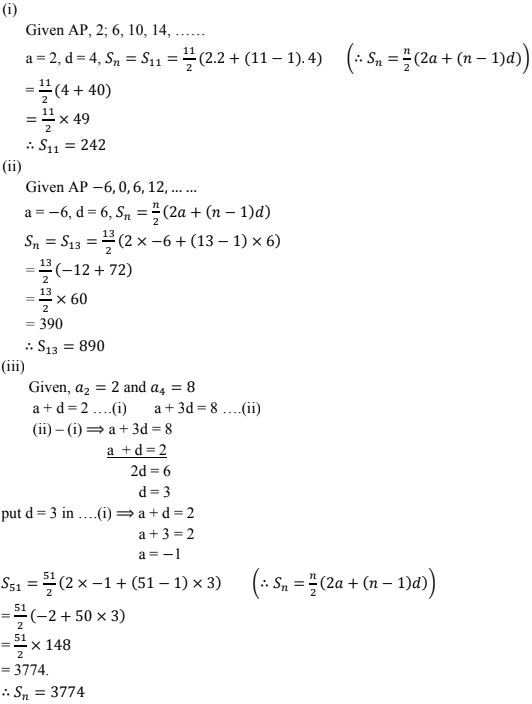
22. Find the sum of 
(i) the first 15 multiples of 8 
(ii) the first 40 positive integers divisible by (a) 3 (b) 5 (c) 6. 
(iii) all  3 digit natural numbers which are divisible by 13. 
(iv) all 3 - digit natural numbers, which are multiples of 11. 

Solution

The first 15 multiples of 8 are 8, 16, 24, ..... 
a = 8, d = 8, n = 15 

23. Find the sum : 
(i) 2 + 4 + 6+ ....... + 200
(ii) 3 + 11 + 19+ ...... + 803 
(iii) 34 + 32 + 30 + ...... + 10 
(iv) 25 + 28 + 31 + ..... + 100

Solution

24. Find the sum of the first 15 terms of each of the following sequence having nth term as 

(i) a_n = 3 + 4n
(ii) b_n = 5 + 2n
(iii) Y_n = 9 - 5n

Solution

25. Find the sum of first 20 terms of the sequence whose nth term is a = An + B. 

Solution

26. Find the sum of the first 25 terms of an A.P. whose nth term is given by a_n = 2 - 3n.

Solution

27. Find the sum of the first 25 terms of an A.P. whose nth term is given by a_n = 7 - 3n. 

Solution

28. Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18 respectively. 

Solution

29. If the sum of 7 terms of an A.P. is 49 and that of 17 terms is 289, find the sum of n terms. 

Solution

30. The first term of an A.P. is 5, the last term is 45 and the sum is 400. find the number of terms and the common difference. 

Solution

31. In an A.P., the sum of first n terms is 3n² /2 + 13n/2 . Find its 25th term. 

Solution

32. Let there be an A.P. with first term 'a' common difference 'd'. If a denotes its nth term and s_n the sum of first n terms, find. 

(i) n and s_n and if a = 5, d = 3 and a = 50 
(ii) n and a, if a_n = 4, d = 2 and s_n = -14
(iii) d, if a = 3, n = 8 and s_n = 192
(iv) a, if a_n = 28, s_n = 144 and n = 9 
(v) n and d, if a = 8, a = 62 and s_n = 210 
(vi) n and a_n , if a = 2, d = 8 and s_n = 90

Solution

33. A man saved Rs 16500 in ten years. In each years after the first he saved Rs 100 more than he did in the preceding year. How much did he save in the first year ? 

Solution

Let 'a' be the money he saved in first year 
⇒ First year he saved the money = Rs a 
He saved Rs 100 more than, he did in preceding year. 
⇒ Second year he saved the money = Rs (a + 100)
⇒ Third year he saved the money = Rs. (a + 2(100)]

So, the sequence is a, a + 100, a + 2(100), ....., This is in AP with common difference (d) = 100.
⇒ Sum of money he saved in 10 years s₁₀ = 16500 rupees 

34. A man saved Rs 32 during the first year, Rs 36 in the second year and in this way he increases his saving by Rs 4 every year. Find in what time his saving will be Rs 200. 

Solution

35. A man arranges to pay off a debt of Rs 3600 by 40 annual installments which form an arithmetic series. When 30 of the installments are paid, he dies leaving one -third of the debt unpaid, find the value of the first installment. 

Solution

Given, 
A man arranges to pay off a debt of Rs 3600 by 40 annual installments which form an A.P. 
i.e., sum of all 40 installments = Rs 3600 
 s₄₀ = 3600 
Let, the money he paid in first installment is a, and every year he paid with common difference  =d 
Then, 

but, 
He died by leaving one third of the debt unpaid that means he paid remaining money in 30 installments. 
∴ The money he paid in 30 installments = 3600 - 3600/3 = 3600 - 1200 = 2400
∴ s₃₀ = 2400