RD Sharma Solutions Chapter 10 Circles Exercise 10.2 Class 10 Maths

Chapter Name | RD Sharma Chapter 10 Circles |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 10.2 Solutions
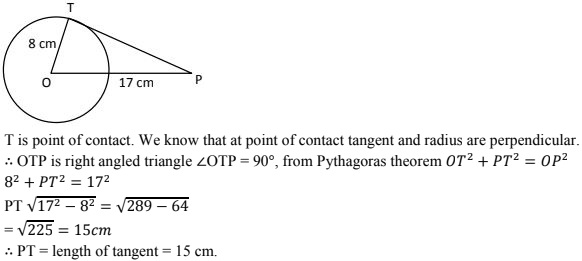
1. If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Solution
OT = radius = 8 cm
OP = 17 cm
PT = length of tangent = ?
2. Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
Solution
Consider a circle with center O.
OP = radius = 5cm.
A tangent is drawn at point P, such that line through O intersects it at Q, OB = 13cm.
Length of tangent PQ = ?
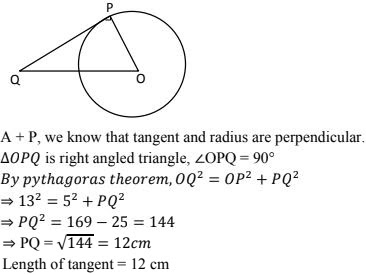
3. A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
Solution
Given OP = 26 cm
PT = length of tangent = 10 cm
radius = OT = ?
XY is the common chord.
Suppose 'A' is a point on the common chord and AM and AN be the tangents drawn A to the circle.

"Let PT be a tangent to the circle from an external point P and a secant to the circle through P intersects the circle at points A and B, then PT2 = PA × PB"
Now AM is the tangent and AXY is a secant
AN is a tangent and AXY is a secant
∴ AM = AN

We know that
The tangents drawn from same external points to the circle are equal in length.
1. Consider tangents from point A [AM ⊥ AE]
AH = AE ...(i)
2. From point B [EB & BF]
BF = EB ...(ii)
3. From point C [CF & GC]
FC = CG ...(iii)
4. From point D [DG & DH]
DH = DG ...(iv)
Adding (i), (ii), (iii), & (iv)
(AH + BF + FC + DH) = [(AC + CB) + (CG + DG)]
⇒ (AH + DH) + (BF + FC) = (AE + EB) + (CG + DG)
⇒ AD + BC = AB + DC [from fig.]
Sum of one pair of opposite sides is equal to other.



∠APB = 60°
Represented in the figure
We know that

A line drawn from center to point from where external tangents are drawn divides or bisects the angle made by tangents at that point ∠APO = ∠OPB = 1/2 × 60° = 30°
The chord AB will be bisected perpendicularly
∴ AB = 2AM
In ΔAMP,

Perimeter of ΔPCD = PC + PD + CD = PC + PD + CE + ED

We know that
The two tangents drawn from external point to the circle are equal in length.
From point P, PA = PB = 14 cm
From point C, CE = CA
From, point D, DB = ED
Perimeter = PC + PD + CA + DB
= PA + PB = 14 + 14 = 28 cm.
As ABC is right angled triangle

AC = 10 cm
Consider BQOP ∠B = 90° ,
∠BPO = ∠OQB = 90° [At point of contact, radius is perpendicular to tangent]
All the angles = 90° & adjacent sides are equal
∴ BQOP is square BP = BQ = r
We know that
The tangents drawn from any external point are equal in length.
AP = AR = AB - PB = 8 - r
QC = RC = BC - BQ = 6 - r
AC = AR + RC ⇒ 10 = 8 - r + 6 - r
⇒ 10 = 14 - 2r
⇒ 2r = 4
⇒ Radius = 2 cm
Tangents drawn from external point to the circle are equal in length PA = PB


14. If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.

We know that
The tangents from external point to circle are equal in length
From point A, AP = AQ
But AB = AC
⇒ PB = PC ...(i)
From B, PB = BL ...(ii)
from C, CL = CQ ...(iii)
From (i), (ii) & (iii)
BL = CL
∴ L bisects BC.


The at point of contact, the tangent is perpendicular to the radius is line from center to point on circle. Therefore, perpendicular to tangent will pass through center of circle.
O is center of circle
BCD is tangent.


Let the circles be represented by (i) & (ii) respectively
TQ, TP are tangents to (i)
TP, TR are tangents to (ii)
We know that
The tangents drawn from external point to the circle will be equal in length.
For circle (i), TQ = TP ...(i)
For circle (ii), TP = TR ...(ii)
From (i) & (ii) TQ = TR
AB = 29 cm
∠ B = 90°
DS = 5 cm

From fig in quadrilateral POQB
∠OPB = ∠OQB = 90° = ∠B = ∠POQ
and PO = OQ
∴ POQB is a square PB = BQ = r
We know that
Tangents drawn from external point to circle are equal in length.
We know that
Tangents drawn from external point to circle are equal in length.
We know that
Tangents drawn from external point to circle are equal in length.
From A, AR = AQ ...(i)
From B, PB = QB ...(ii)
From C, PC = CS ...(iii)
From D, DR = DS ...(iv)

20. In fig. there are two concentric circles with Centre O of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles if AP = 12 cm, find the tangent length of BP.

Radius OB = OA = 10 cm.

Let line through Centre to point from where tangents are drawn be intersecting chord AB at M. we know that the line joining Centre to point from where tangents are drawn be intersecting chord AB at M. we know that the line joining Centre to point from where tangents are drawn bisects the chord joining the points on the circle where tangents intersects the circle.

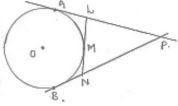
Given
O is Centre of circle
PA and PB are tangents
We know that
The tangents drawn from external point to the circle are equal in length.
From point P, PA = PB
⇒ PL + AL = PN + NB ...(i)
From point L & N, AL = LM and MN = NB
PL + LM = PN + MN
Hence proved.



Given
BC is tangent to circle
OE bisects AP, AE = EP
Consider ΔAOP