RS Aggarwal Solutions Chapter 8 Trigonometric Identities MCQ Class 10 Maths

Chapter Name | RS Aggarwal Chapter 8 Trigonometric Identities |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Trigonometric Identities MCQ Solutions
1. (cos2 56° + cos2 34°)/(sin2 56° + sin2 34°) + 3 tan2 56° tan2 34° = ?
(a) 3.1/2
(b) 4
(c) 6
(d) 5
Solution
(cos2 56° + cos2 34°)/(sin2 56° + sin2 34°) + 3 tan2 56° tan2 34°
= {cos(90° - 34°)}2 + cos2 34°}/{sin(90° - 34°)}2 + sin2 34° + 3{tan(90° - 34°)}2 tan2 34°
= (sin2 34° + cos2 34°)/(cos2 34° + sin2 34°) + 3 cot2 34° tan2 34°
[∵ cos (90° - θ) = sin θ, sin (90° – θ) = cos θ and tan (90° - θ) = cot θ]
= 1/1 + 3 × 1 [∵ cot θ = 1/tan θ and sin2 θ + cos2 θ = 1]
= 4
2. The value of (sin2 30° cos2 45° + 4 tan2 30° + 1/2 sin2 90° + 1/8 cot2 60°) = ?
(a) 3/8
(b) 5/8
(c) 6
(d) 2
Solution
(d) 2
(sin2 30° cos2 45°) + 4 tan2 30° + 1/2 sin2 90° + 1/8 cot2 60°
= 1/22 × 1/(√2)2 + 4 × 1/(√3)2 + 1/2 × 12 + 1/8 × 1/(√3)2
[∵ sin 30° = 1/2 and cos 45° = 1/√2 and tan 30° = 1/2 and cot 60° = 1/√3]
= 1/4 × 1/2 + 4 × 1/3 + 1/2 + 1/24
= 1/8 + 4/3 + 1/2 + 1/24
= 1/8 + 4/3 + 1/2 + 1/24
= (3 + 32 + 12 + 1)/24
= 48/24
= 2
3. If cos A + cos2 A = 1 then (sin2 A + sin4 A) = ?
(a) 1/2
(b) 2
(c) 1
(d) 4
Solution
cos2 A + A = 1
⇒ cos A = sin2 A ....(i)
Squaring both sides of (i), we get:
cos2 A = sin4 A ...(ii)
Adding (i) and (ii), we get:
sin2 A + sin4 A = cos A + cos2 A
⇒ sin2 A + sin4 A = 1 [∵ cos A + cos2 A = 1]
4. If sin θ = √3/2 then (cosec θ + cot θ) = ?
(a) (2 + √3)
(b) 2√3
(c) √2
(d) √3
Solution
(d) √3
Given: sin θ = √3/2 and cosec θ = 2/√3
cosec2 θ – cot2 θ = 1
⇒ cot2 θ = cosec2 θ – 1
⇒ cot2 θ = 4/3 – 1 [Given]
⇒ cot θ = 1/√3
∴ cosec θ + cot θ = 2/√3 + 1/√3
= 3/√3
= (√3 × √3)/√3
= √3
5. If cot A = 4/5, prove that (sin A + cos A)/(sin A – cos A) = 9.
Solution
Given: cot A = 4/5
Writing cot A = cos A/sin A and squaring the equation, we get:
cos2 A/sin2 A = 16/25
⇒ 25 cos2 A = 16 sin2 A
⇒ 25 cos2 A = 16 – 16 cos2 A
= cos2 A = 16/41

Solution
Given:
2x = sec A
⇒ x = sec A/2 ...(i)
and 2/x = tan A
⇒ 1/x = tan A ...(ii)
∴ x + 1/x = sec A/2 + tan A/2 [∵ From (i) and (ii)]
Also, x – 1/x = sec A/2 – tan A/2
∴ (x + 1/x)(x – 1/x) = (sec A/2 + tan A/2)(sec A/2 – tan A/2)
⇒ x2 – 1/x2 = 1/4 (sec2 A – tan2 A)
∴ x2 – 1/x2 = 1/4 × 1 (∵ sec2 A – tan2 A = 1)
= 1/4
Hence proved.
7. If √3 tan θ = 3 sin θ, prove that (sin2 θ – cos2 θ) = 1/3.
Solution
Given: √3 tan θ = 3 sin θ
⇒ √3/cos θ = 3 [∵ tan θ = sin θ/cos θ]
⇒ cos θ = √3/2
⇒ cos2 θ = 3/9
∴ sin2 θ = 1 – 3/9
⇒ sin2 θ = 6/9
∴ LHS = sin2 θ – cos2 θ
= 6/9 - 3/9 [∴ sin2 θ = 6/9, cos2 θ = 3/9]
= 3/9
= 1/3
= RHS
Hence proved.
8. Proved that (sin2 73° + sin2 17°)/(cos2 28° + cos2 62°) = 1.
Solution
(sin2 73 + sin2 17°)/(cos2 28° + cos2 62°) = 1
LHS = (sin2 73° + sin2 17°)/(cos2 28° + cos2 62°)
= [sin (90° - 17°)]2 + sin2 17°)/[cos(90° - 62°)]2 + cos2 62°
= cos2 17° + sin2 17°)/(sin2 62° + cos2 62°)
= 1/1 [∵ sin2 + cos2 θ = 1]
= 1
= RHS
9. If 2 sin 2θ = √3, prove that θ = 30°.
Solution
2 sin (2θ) = √3
⇒ sin (2θ) = √3/2
⇒ sin (2θ) = sin (60°)
⇒ 2θ = 60°
⇒ θ = 60°/2
⇒ θ = 30°
10. Prove that = (cosec A + cot A).
Solution

= 1/sin A + cos A/sin A
= cosec A + cot A = RHS
Hence proved.
11. If cosec θ + cot θ = p, prove that cos θ = (p2 – 1)/(p2 + 1).
Solution
cosec θ + cot θ = p
⇒ 1/sin θ + cos θ/sin θ = p
⇒ (1 + cos θ)/sin θ = p
Squaring both sides, we get:
(1 + cos θ/sin θ)2 = p2
⇒ (1 + cos θ/sin2 θ)2 = p2
⇒ (1 + cos θ)2/(1 – cos2 θ) = p2
⇒ (1 + cos θ)2/(1 + cos θ)(1 – cos θ) = p2
⇒ (1 + cos θ )/(1 – cos θ) = p2
⇒ 1 + cos θ = p2(1 – cos θ)
⇒ 1 + cos θ = p2 – p2 cos θ
⇒ cos θ (1 + p2) = p2 – 1
⇒ cos θ = (p2 – 1)/(p2 + 1)
Hence proved.
12. Prove that (cosec A – cot A)2 = (1 – cos A)/(1 + cos A).
Solution
(cosec A – cot A)2 = (1 – cos A)/(1 + cos A).
LHS = (cosec A – cot A)2
= (1/sin A – cos A/sin A)2
= (1 – cos A/sin A)2
= (1 – cos A)2/sin2 A
= (1 – cos A)2/(1 – cos2 A) [∵ sin2 θ + cos2 θ = 1]
= (1 – cos A)(1 – cos A)/(1 – cos A)(1 + cos A)
= (1 – cos A)/(1 + cos A)
= RHS
Hence proved.
13. If 5 cot θ = 3, show that the value of (5 sin θ – 3 cos θ)/(4 sin θ + 3 cos θ) is 16/29.
Solution
Given 5 cot = 3
⇒ 5 cos θ/sin θ = 3 [∵ cot θ = cos θ/sin θ]
⇒ 5 cos θ = 3 sin θ
Squaring both sides, we get:
25 cos2 θ = 9 sin2 θ
⇒ 25 cos2 θ = 9 – 9 cos2 θ [∵ sin2 θ + cos2 θ = 1]
⇒ 34 cos2 θ = 9

Solution
(sin 32° cos 58° + cos 32° sin 58°) = 1
LHS = sin 32° cos 58° + cos 32° sin 58°
= sin (90° - 58°) cos 58° + cos(90° - 58°) sin 58°
= cos 58° × cos 58° + sin 58° × sin 58° [∵ sin(90° - θ) = cos θ, cos (90° - θ) = sin θ]
= cos2 58° + sin2 58°
= 1 [∵ sin2 θ + cos2 θ = 1]
= RHS
15. If x = a sin θ + b cos θ and y = a cos θ – b sin θ, prove that x2 + y2 = a2 + b2.
Solution
Given: x = a sin θ + b cos θ
Squaring both sides, we get:
x2 = a2 sin2 θ + 2ab sin θ cos θ + b2 cos2 θ ...(i)
Also, y = a cos θ – b sin θ
Squaring both sides, we get:
y2 = a2 cos2 θ – 2ab sin θ cos θ + b2 sin2 θ ...(ii)
∴ LHS = x2 + y2
= a2 sin2 + 2absin θ cos θ + b2 cos2 θ + a2 cos2 θ – 2ab sin θ cos θ + b2 sin2 θ
[using (i) and (ii)]
= a2 (sin2 θ + cos2 θ) + b2(sin2 θ + cos2 θ)
= a2 + b2 [∵ sin2 θ + cos2 θ = 1]
= RHS
Hence proved.
16. Proved that (1 + sin θ)/(1 – sin θ) = (sec θ + tan θ)2.
Solution
(1 + sin θ)/(1 – sin θ) = (sec θ + tan θ)2
LHS = (1 + sin θ)/(1 – sin θ)
Multiplying the numerator and denominator by (1 = sin θ), we get
(1 + sin θ)2/(1 – sin2 θ)
= (1 + 2 sin θ + sin2 θ)/cos2 θ [∵ sin2 θ + cos2 θ = 1]
= sec2 θ + 2 × sin θ/cos θ × sec θ + tan2 θ
= sec2 θ + 2 × tan θ × sec θ + tan2 θ
= (sec θ + tan θ)2
= RHS
Hence proved.
17. Prove that 1/(sec θ – tan θ) – 1/cos θ = 1/cos θ = 1/(sec θ + tan θ).
Solution
1/(sec θ – tan θ) – 1/cos θ = 1/cos θ = 1/(sec θ + tan θ)
LHS = 1/(sec θ – tan θ) – 1/cos θ
= (sec θ + tan θ)/(sec2 θ – tan2 θ) – sec θ [∵ sec2 θ – tan2 θ = 1]
= tan θ
RHS = 1/cos θ – 1/(sec θ + tan θ)
= sec θ – (sec θ – tan θ)/(sec2 θ – tan2 θ) (Multiplying the numerator and denominator by (sec θ – tan θ)
= sec θ + tan θ – sec θ [∵ sec2 θ – tan2 θ = 1]
= tan θ
∴ LHS = RHS
Hence proved.
18. Prove that (sin A – 2 sin3 A)/(2 cos3 A – cos A) = tan A
Solution
LHS = (sin A – 2 sin3 A)/(2 cos3 A – cos A)
= sin A(1 – 2 sin2 A)/cos A(2 cos2 A – 1)
= tan A{(sin2 A + cos2 A – 2 sin2 A)/(2 cos2 A – sin2 A – cos2 A)} [∵ sin2 A + cos2 A = 1]
= tan A{(cos2 A – sin2 A)/(cos2 A – sin2 A)}
= tan A
= RHS
19. Prove that tan A/(1 – cot A) + cot A/(1 – tan A) = (1 + tan A + cot A).
Solution
LHS = tan A/(1 – cot A) + cot A/(1 – tan A)
= tan A/(1 – cot A) + cot2 A/(cot A – 1) [∵ tan A = 1/cot A]
= tan A/(1 – cot A) – cot2 A/(1 – cot A)
= (tan A – cot2 A)/(1 – cot A)
= 1/(cot A) – cot2 A/(1 – cot A)
= (1 – cot3 A)/cot A(1 - cot A)
= (1 – cot A)(1 + cot A + cot2 A)/cot A(1 – cot A) [∵ a3 - b3 = (a – b)(a2 + ab + b2)]
= 1/cot A + cot2 A/cot A + cot A/cot A
= 1 + tan A + cot A
= RHS
Hence proved.
20. If sec 5A = cosec (A - 36°) and 5A is an acute angle, show that A = 21°.
Solution
Given: sec 5A = cosec (A - 36°)
⇒ cosec(90° - 5A) = cosec(A - 36°) [∵ cosec (90° - θ) = sec θ]
⇒ 90° - 5A = A - 36°
⇒ 6A = 90° + 36°
⇒ 6A = 126°
⇒ A = 21°
Multiple choice Questions
1. sec 30°/cosec 60° = ?
(a) 2/√3
(b) √3/2
(c) √3
(d) 1
Solution
(d) 1
Sec 30°/cosec 60°
= sec 30°/(sec 90° - 60°)
= sec 30°/sec 30°
= 1
2. tan 35°/cot 55° + cot 78°/tan 12° = ?
(a) 0
(b) 1
(c) 2
(d) none of these
Solution
(c) 2
We have:
tan 35°/cot 35° + cot 78°/tan 12°
tan 35°/cot(90° - 35°) + cot(90° - 12°)/tan 12°
= tan 35°/tan 35° + tan 12°/tan 12° [∵ cot(90° - θ)]
= 1 + 1
= 2
3. tan 10° tan 15° tan 75° tan 80° = ?
(a) √3
(b) 1/√3
(c) –1
(d) 1
Solution (d) 1
We have,
tan 10° tan 15° tan 75° tan 80°
= tan 10° × tan 15° × tan (90° - 15°) × tan (90° - 10°)
= tan 10° × tan 15° cot 15° × cot 10° [∵ tan(90° - θ) = cot θ]
= 1
4. tan 5° tan 25° tan 30° tan 65° tan 85° = ?
(a) √3
(b) 1/√3
(c) 1
(d) none of these
Solution
(b) 1/√3
We have:
tan 5° tan 25° tan 30°.tan 65° tan 85°
= tan 5° tan 25° tan 30° tan (90° - 25°) tan (90° - 5°)
= tan 5° tan 25° × 1/√3 × cot 25° cot 5° [∵ tan(90° - θ) = cot θ and tan 30° = 1/√3]
= 1/√3
5. cos 1° cos 2° cos 3° ...... cos 180° = ?
(a) -1
(b) 1
(c) 0
(d) 1/2
Solution (c) 0
cos 1° cos2° cos 3° ...... cos 180°
cos 1° cos 2° cos 3° .......cos 90° .......cos (180)°
= 0 [∵ cos 90° = 0]
6. (2 sin2 63° + 1 + 2 sin2 27°)/(3 cos2 17° - 2 + 3 cos2 73°) = ?
(a) 3/2
(b) 2/3
(c) 2
(d) 3
Solution
(d) 3
Given: (2 sin2 63° + 1 + 2 sin2 27°)/(3 cos2 17° - 2 + 3 cos2 73°)
= [2(sin2 63° + sin2 27°) + 1]/[3(cos2 17° + cos2 73°) – 2]
= 2[sin2 63° + sin2(90° - 63°) + 1]/3[cos2 17° + sin2 17°] – 2)
= 2(sin2 63° + cos2 63°) + 1/3(cos2 17° + sin2 17°) – 2
[∵ sin(90° - θ) = cos θ and cos (90° - θ) = sin θ]
= (2 × 1 + 1)/(3 × 1 – 2) [∵ sin2 θ + cos2 θ = 1]
= (2 + 1)/(3 – 2)
= 3/1
= 3
7. sin 47° cos 43° + cos 47° sin 43° = ?
(a) sin 4°
(b) cos 4°
(c) 1
(d) 0
Solution
(c) 1
(sin 43° cos 47° + cos 43° sin 47°)
= sin 43° cos (90° - 43°) + cos 43° sin(90° - 43°)
= sin 43° sin 43° + cos 43° sin 43° [∵ cos(90° - θ) = sin θ and sin(90° - θ) = cos θ]
= sin2 43° + cos2 43°
= 1
8. sec 70° sin 20° + cos 20° cosec 70° = ?
(a) 0
(b) 1
(c) -1
(d) 2
Solution
(d) 2
We have:
sec 70° sin 20° + cos 20°cosec 70°
= sin 20°/cos 70° + cos 20°/sin 70°
= sin 20°/cos(90° - 20°) + cos 20°/sin(90° - 20°)
= sin 20°/sin 20° + cos 20°/cos 20° [∵ cos(90° - θ) = sin θ and sin (90° - θ) = cos θ]
= 1 + 1
= 2
OR
sec 70° sin 20° + cos 20° cosec 70°
= cosec(90° - 70°) sin 20° + cos 20° sec (90° - 70°)
= cosec 20° sin 20° + cos 20° sec 20°
= 1/sin 20° × sin 20° + cos 20° × 1/cos2 0°
= 1 + 1
= 2
9. If sin 3A = cos (A - 10°) and 3A is acute then ∠A = ?
(a) 35°
(b) 25°
(c) 20°
(d) 45°
Solution
(b) 25°
We have:
[sin 3A = cos(A - 10°)]
⇒ cos(90° - 3A) = cos(A - 10°) [∵ sin θ = cos(90° - θ)]
⇒ 90° - 3A = A - 10°
⇒ -4A = - 100
⇒ A = 100/4
⇒ A = 25°
10. If sec 4A = cosec (A - 10°) and 4A is acute then ∠A = ?
(a) 20°
(b) 30°
(c) 30°
(d) 50°
Solution
(a) 20°
We have,
sec 4A = cosec(A - 10°)
⇒ cosec (90° - 4A) = cosec(A - 10°)
Comparing both sides, we get
90° - 4A = A - 10°
⇒ 4A + A = 90° + 10°
⇒ 5A = 100°
⇒ A = 100°/5
∴ A = 20°
11. If A and B are acute angles such that sin A = cos B then (A + B) = ?
(a) 45°
(b) 60°
(c) 90°
(d) 180°
Solution
(c) 90°
12. If cos (α + β) = 0 then sin (α – β) = ?
(a) sin α
(b) cos β
(c) sin 2α
(d) cos 2β
Solution
(d) cos 2β
We have:
cos (α + β) = 0
⇒ cos(α + β) = cos 90°
⇒ α + β = 90°
⇒ α = 90° - β ...(i)
Now, sin (α – β)
= sin [(90° - β) – β] [Using (i)]
= sin (90° - 2β)
= cos 2β [∵ sin(90° - θ) = cos θ]
14. sec2 10° - cot2 80°
(a) 1
(b) 0
(c) 3/2
(d) 1/2
Solution
(a) 1
We have (sin 79° cos 11° + cos 79° sin 11°)
= sin 79° cos(90° - 79°) + cos 79° sin(90° - 79°)
= sin 79° sin 79° + cos 79° cos 79° [∵ cos (90° - θ) = sin θ and sin(90° – θ) = cos θ]
= sin2 79° + cos2 79°
= 1
15. cosec2 57° - tan2 33° = ?
(a) 0
(b) 1
(c) – 1
(d) 2
Solution
We have:
(cosec2 57° - tan2 33°)
= [cosec2(90° - 33°) – tan2 33°]
= (sec2 33° - tan2 33°) [∵ cosec(90° - θ) = sec θ]
= 1 [∵ sec2 θ – tan2 θ = 1]
16. 2 tan2 30° sec2 52° sin2 38°)/(cosec2 70° - tan2 20°) = ?
(a) 2
(b) 1/2
(c) 2/3
(d) 3/2
Solution
We have:
[(2 tan2 30° sec2 52° sin2 38°)/(cosec2 70° - tan2 20°)]
= [2 × (1/√3)2 sec2 52°[sin2(90° - 52°)}/{cosec2 (90° - 20°)} – tan2 20°]
= [2/3 × (sec2 52°.cos2 52°/sec2 20° - tan2 20°)] [∵ sin (90° - θ) = cos θ and cosec(90° - θ) = sec θ]
= 2/3 × 1/1 [∵ sec2 θ – tan2 θ = 1]
= 2/3
17. {(sin2 22° + sin2 68°)/(cos2 22° + cos2 68°) + sin2 63° + cos 63° sin 27°} = ?
(a) 0
(b) 1
(c) 2
(d) 3
Solution
We have:
[(sin2 22° + sin2 68°/cos2 22° + cos2 68°) + sin2 63° + cos 63° sin 27°]
= {sin2 22° + sin2(90° - 22°)/cos2(90° - 68°) + cos2 68°} + sin2 63° + cos 63° {sin(90° - 63°)}]
= [sin2 22° + cos2 22°/sin2 68° + cos2 68° + sin2 63° + cos 63° cos 63°] [∵ sin(90° - θ)]
= cos θ and cos (90° - θ) = sin θ]
= [1/1 + sin2 63° + cos2 63°] [∵ sin2 θ + cos2 θ = 1]
= 1 + 1
= 2
18. [cot(90° - θ).sin(90° - θ)]/sin θ + cot 40°/tan 50° - (cos2 20° + cos2 70°) = ?
(a) 0
(b) 1
(c) – 1
(d) none of these
Solution
We have:
[cot(90° - θ). sin(90° - θ)/sin θ + cot 40°/tan 50° - (cos2 20° + cos2 70°)]
= tan θ. cos θ/cos θ + cot (90° - 50°)/tan 50° - {cos2 (90° - 70°) + cos2 70°}] [∵ cot (90° - θ) = tan θ and sin(90° - θ) = cos θ]
= [sin θ/sin θ + tan 50°/tan 50° - (sin2 70° + cos2 70°)] [∵ cos(90° - θ) = sin θ]
= (sin θ/sin θ + 1 – 1)
= 1 + 1 – 1
= 1
19. (cos 38° cosec 52°)/(tan 18° tan 35° tan 60° tan 72° tan 55° = ?
(a) √3
(b) 1/3
(c) 1/√3
(d) 2/√3
Solution
(c) 1/√3
We have:
[(cos 38° cosec 52°)/(tan 18° tan 35° tan 60° tan 72° tan 55°)]
= cos 38° cosec(90° - 38°)/[tan 18° tan 35° × √3 × tan(90° - 18°)tan(90° - 35°)] [∵ cos(90° - θ) = sec θ and tan (90° - θ) = cot θ]
= [cos 38° sec 38°]/[tan 18° tan 35° × √3 × cot 18° cot 35°]
= [1/sec 38° × sec 38°]/[1/(cot 18° cot 35°) × √3 cot 18° cot 35°]
= 1/√3
20. If 2 sin 2θ = √3 then θ = ?
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution
(a) 30°
2 sin 2θ = √3
⇒ sin 2θ = √3/2 = sin 60°
⇒ sin 2θ = sin 60°
⇒ 2θ = 60°
⇒ θ = 30°
21. If 2 cos 3θ = 1 then θ = ?
(a) 10°
(b) 15°
(c) 20°
(d) 30°
Solution
2 cos 3θ = 1
⇒ cos 3θ = 1/2
⇒ cos 3θ = cos 60° [∵ cos 60° = 1/2]
⇒ 3θ = 60°
⇒ θ = 60°/3 = 20°
22. If √3 tan 2θ – 3 = 0 then θ = ?
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Solution
√3 tan 2θ – 3 = 0
⇒ √3 tan 2θ = 3
⇒ tan 2θ = 3/√3
⇒ tan 2θ = √3 [∵ tan 60° = √3]
⇒ tan 2θ = tan 60°
⇒ 2θ = 60°
⇒ θ = 30°
23. If tan x = 3 cot x then x = ?
(a) 45°
(b) 60°
(c) 30°
(d) 15°
Solution
(b) 60°
tan x = 3 cot x
⇒ tan x/cot x = 3
⇒ tan2 x = 3 [∵ cot x = 1/tan x]
⇒ tan x = √3 = tan 60°
⇒ x = 60°
24. If x tan 45° cos 60° = sin 60° then x = ?
(a) 1
(b) 1/2
(c) 1/√2
(d) √3
Solution
(a) 1
x tan 45° cos 60° = sin 60° cot 60°
⇒ x(1)(1/2) = (√3/2)(1/√3)
⇒ x(1/2) = (1/2)
⇒ x = 1
25. If tan2 45° - cos2 30° = x sin 45° cos 45° then x = ?
(a) 2
(b) -2
(c) 1/2
(d) -1/2
Solution
(c) 1/2
(tan2 45° - cos2 30°) = x sin 45° cos 45°
⇒ x = (tan2 45° - cos2 30°)/(sin 45° cos 45°)
= [(1)2 – (√3/2)2]/(1/√2 × 1/√2)
= (1 – 3/4)/(1/2)
= (1/4)/(1/2)
= 1/4 × 2
= 1/2
26. sec2 60° - 1 = ?
(a) 2
(b) 3
(c) 4
(d) 0
Solution
(b) 3
sec2 60° - 1
= (2)2 – 1
= 4 – 1
= 3
27. (cos 0° + sin 30° + sin 45°)(sin 90° + cos 60° - cos 45°) = ?
(a) 5/6
(b) 5/8
(c) 3/5
(d) 7/4
Solution
(a) 7/4
(cos 0° + sin 30° + sin 45°)(sin 90° + cos 60° - cos 45°)
= (1 + 1/2 + 1/√2)(1 + 1/2 – 1/√2)
= (3/2 + 1/√2)(3/2 – 1/√2)
= [(3/2)2 – (1/√2)2]
= (9/4) – (1/2)
= (9 – 2)/4
= 7/4
28. sin2 30° + 4 cot2 45° - sec2 60° = ?
(a) 0
(b) 1/4
(c) 4
(b) 1
Solution
(b) 1/4
(sin2 30° + 4 cot2 45° - sec2 60°)
= [(1/2)2 + 4 × (1)2 – (2)2]
= (1/4 + 4 – 4)
= 1/4
29. 3 cos2 60° + 2 cot2 30° - 5 sin2 45° = ?
(a) 13/6
(b) 17/4
(c) 1
(d) 4
Solution
(b) 17/4
(3 cos2 60° + 2 cot2 30° - 5 sin2 45°)
= [3 × (1/2)2 + 2 × (√3)2 – 5 × (1/√2)2]
= [3/4 + 6 – 5/2]
= (3 + 24 – 10)/4
= 17/4
30. cos2 30° cos2 45° + 4 sec2 60° + 1/2 cos2 90° - 2 tan2 60° = ?
(a) 73/8
(b) 75/8
(c) 81/8
(d) 83/8
Solution
(d) 83/8
(cos2 30° cos2 45° + 4 sec2 60° + 1/2 cos2 90° - 2 tan2 60°)
= [(√3/2)2 × (1/√2)2 + 4 × (2)2 + 1/2 × (0)2 – 2 × (√3)2]
= [(3/4 × 1/2) + 16 – 6]
= [3/8 + 10]
= (3 + 80)/8
= 83/8
31. If cosec θ = √10 then sec θ = ?
(a)
(b)


Solution
(b)
Let us first draw a right ∆ABC right angled at B and ∠A = θ

32. If tan θ = 8/15 then cosec θ = ?
(a) 17/8
(b) 8/17
(c) 17/15
(d) 15/17
Solution
(a) 17/8
Let us first draw a right ∆ABC right angled at B and ∠A = θ.
Give: tan θ = 8/5, but tan θ = BC/AB
So, BC/AB = 8/15
Thus, BC = 8k and AB = 15k

Using Pythagoras theorem in triangle ABC, we have:
AC2 = AB2 + BC2
⇒ AC2 = (15k)2 + (8k)2
⇒ AC2 = 289k2
⇒ AC = 17k
∴ cosec θ = AC/BC = 17k/8k
= 17/8
33. If sin θ = b/a then cos θ = ?
(a)
(b)
(d) b/a
Solution
(b)
Let us draw a right ∆ABC right angled at B and ∠A = θ.
Given: sin θ = a/b, but sin θ = BC/AC
So, BC/AC = a/b
Thus, BC = ak and AC = bk

AC2 = AB2 + BC2
⇒ AB2 = AC2 – BC2
⇒ AB2 = (bk)2 – (ak)2
⇒ AB2 = (b2 – a2)k2

(a) 2/√3
(b) √3/2
(c) 1/2
(d) 2
Solution
(d) 2
Let us first draw a right ∆ABC right angled at B and ∠A = θ.
Give: tan θ = √3
But tan θ = BC/AB
so, BC/AB = √3/1
Thus, BC = √3k and AB = k

Using Pythagoras theorem, we get:
AC2 = AB2 + BC2
⇒ AC2 = (√3k)2 + (k)2
⇒ AC2 = 4k2
⇒ AC = 2k
∴ sec θ = AC/AB = 2k/k = 2/1
35. If sec θ = 25/7 then sin θ = ?
(a) 7/24
(b) 24/7
(c) 24/25
(d) none of these
Solution
(c) 24/25
Let us first draw a right ∆ABC right angled at B and ∠A = θ.
Given sec θ = 25/7
But cos θ = 1/sec θ = AB/AC = 7/25
Thus, AC = 25k and AB = 7k

Using Pythagoras theorem, we get:
AC2 = AB2 + BC2
⇒ BC2 = AC2 – AB2
⇒ BC2 = (25k)2 – (7k)2
⇒ BC2 = 576k2
⇒ BC = 24k
∴ sin θ = BC/AC = 24k/25k
= 24/25
36. If sin θ = 1/2 then cot θ = ?
(a) 1/√3
(b) √3
(c) √3/2
(d) 1
Solution
(b) √3
Given: sin θ = 1/2, but sin θ = BC/AC
So, BC/AC = 1/2
Thus, BC = k and AC = 2k
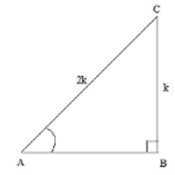
Using Pythagoras theorem in triangle ABC, we have:
AC2 = AB2 + BC2
AB2 = AC2 – BC2
AB2 = (2k)2 – (k2)
AB2 = 3k2
AB = √3k
So, tan θ = BC/AB = k/√3k = 1/√3
∴ cot θ = 1/ tan θ = √3
37. If cos θ = 4/5 then tan θ = ?
(a) 3/4
(b) 4/3
(c) 3/5
(d) 5/3
Solution
(a) 3/4
Since cos θ = 4/5 but cos θ = AB/AC
So, AB/AC = 4/5
Thus, AB = 4k and AC = 5k

Using Pythagoras theorem in triangle ABC, we have:
AC2 = AB2 + BC2
⇒ BC2 = (5k)2 – (4k)2
= BC2 = 9k2
⇒ BC = 3k
∴ tan θ = BC/AB = 3/4
38. If 3x = cosec θ and 3/x = cot θ then (x2 – 1/x2) = ?
(a) 1/27
(b) 1/81
(c) 1/3
(d) 1/9
Solution
(c) 1/3
Given: 3x = cosec θ and 3/x = cot θ
Also, we can deduce that x = cosec θ/3 and 1/x = cot θ/3
So, substituting the values of x and 1/x in the given expression, we get:
3(x2 – 1/x2) = 3 (cosec θ/3)2 – (cot θ/3)2)
= 3 (cosec2 θ)/9 – (cot2 θ/9))
3/9 (cosec2 θ – cot2 θ)
= 1/3 [By using the identity: (cosec2 θ – cot2 θ = 1)]
39. If 2x = sec A and 2/x = tan A then 2(x2 – 1/x2) = ?
(a) 1/2
(b) 1/4
(c) 1/8
(d) 1/16
Solution
(a) 1/2
Given: 2x = sec A and 2/x = tan A
Also, we can deduce that x = sec A/2 and 1/x = tan A/2
So, substituting the values of x and 1/x in the given expression, we get:
2(x2 – 1/x2) = 2(sec A/2)2 – (tan A/2)2
= 2((sec2 A/4) – (tan2 A/4))
= 2/4 (sec2 A – tan2 A)
= 1/2 [By using the identity: (sec2 θ – tan2 θ = 1)]
40. If tan θ = 4/3 then (sin θ + cos θ) = ?
(a) 7/3
(b) 7/4
(c) 7/5
(d) 5/7
Solution
(c) 7/5
Let us first draw a right ∆ABC right angled at B and ∠A = θ.
tan θ = 4/3 = BC/AB
So, AB = 3k and BC = 4k

Using Pythagoras theorem, we get:
AC2 = AB2 + BC2
⇒ AC2 = (3k)2 + (4k)2
⇒ AC2 = 25k2
⇒ AC = 5k
Thus, sin θ = BC/AC = 4/5
Ans cos θ = AB/AC = 3/5
∴ (sin θ + cos θ) = (4/5 + 3/5) = 7/5
41. If (tan θ + cot θ) = 5 then (tan2 θ + cot2 θ) = ?
(a) 27
(b) 25
(c) 24
(d) 23
Solution
(d) 23
We have (tan θ + cot θ) = 5
Squaring both sides, we get:
(tan θ + cot θ)2 = 52
⇒ tan2 θ + cot2 θ + 2 tan θ cot θ = 25
⇒ tan2 θ + cot2 θ + 2 = 25 [∵ tan θ = 1/cot θ]
⇒ tan2 θ + cot2 θ = 25 – 2
= 23
42. If (cos θ + sec θ) = 5/2 then (cos2 θ + sec2 θ) = ?
(a) 21/4
(b) 17/4
(c) 29/4
(d) 33/4
Solution
(b) 17/4
Solution
We have (cos θ + sec θ) = 5/2
Squaring both sides, we get:
(cos θ + sec θ)2 = (5/2)2
⇒ cos2 θ + sec2 θ + 2θ = 25/4
⇒ cos2 θ + sec2 θ + 2 = 25/4 [∵ sec θ = 1/cos θ]
⇒ cos2 θ + sec2 θ = 25/4 – 2 = 17/4
43. If tan θ = 1/√7 then (cosec2 θ + sec2 θ)/(cosec2 θ + sec2 θ) = ?
(a) -2/3
(b) -3/4
(c) 2/3
(d) 3/4
Solution
(d) 3/4
(cosec2 θ – sec2 θ)/(cosec2 θ + sec2 θ)
= sin2 θ(1/sin2 θ – 1/cos2 θ)/sin2 θ(1/ sin2 θ + 1/cos2 θ) [Multiplying the numerator and denominator by sin2 θ]
= (1 – tan2 θ)/(1 + tan2 θ)
= (1 – 1/7)/(1 + 1/7)
= 6/8
= 3/4
44. If tan θ = 4 then |(7 sin θ - 3 cos θ)/(7 sin θ + 3 cos θ ) = ?
(a) 1/7
(b) 5/7
(c) 3/7
(d) 5/14
Solution
(a) 1/7
7 tan θ = 4
Now dividing the numerator and denominator of the given expression by cos θ,
We get:
1/cos θ(7 sin θ - 3 cos θ )/1/cos θ(7 sin θ + 3 cos θ)
= (7 tan θ - 3)/(7 tan θ + 3)
= (4 – 3)/(4 + 3) [∵ tan θ = 4]
= 1/7
45. If 3 cot θ = 4 then (5 sin θ + 3 cos θ)/(5 sin θ + 3 cos θ )/(5 sin θ – 3 cos θ) = ?
(a) 1/3
(b) 3
(c) 1/9
(d) 9
Solution
(d) 9
We have (5 sin θ + 3 cos θ)/(5 sin θ – 3 cos θ)
Dividing the numerator and denominator of the given expression by sin θ, we get:
1/sin θ(5 sin θ + 3 cos θ)/1/sin θ(5 sin θ – 3 cos θ)
= (5 + 3 cot θ)/(5 – 3 cot θ)
= (5 + 4)/(5 – 4) = 9 [∵ 3 cot θ = 4]
46. If tan θ = a/b then (a sin θ – b cos θ)/(a sin θ + b cos θ) = ?
(a) (a2 + b2)/(a2 – b2)
(b) (a2 – b2)/(a2 + b2)
(c) a2/(a2 + b2)
(d) a2/(a2 + b2)
Solution
(b) (a2 – b2)/(a2 + b2)
We have tan θ = a/b
Now, dividing the numerator and denominator of the given expression by cos θ we get:
(a sin θ – b cos θ)/(a sin θ + b cos θ)
= [1/cos θ(a sin θ – b cos θ)]/[1/cos θ(a sin θ + b cos θ)]
= (a tan θ – b)/(a tan θ + b)
= (a2/b – b)/(a2/b + b)
= (a2 – b2)/(a2 + b2)
47. If sin A + sin2 A = 1 then cos2 A + cos4 A = ?
(a) 1/2
(b) 1
(c) 2
(d) 3
Solution
(b) 1
sin A + sin2 A = 1
⇒ sin A = 1 – sin2 A
⇒ sin A = cos2 A (∵ 1 – sin2 A)
⇒ sin2 A = cos4 A (Squaring both sides)
⇒ 1 – cos2 A = cos4 A
⇒ cos4 A + cos2 A = 1
48. If cos A + cos2 A = 1 then sin2 A + sin4 A = ?
(a) 1
(b) 2
(c) 4
(d) 3
Solution
(a) 1
cos A + cos2 A = 1
⇒ cos A = 1 – cos2 A
⇒ cos A = sin2 A (∵ 1 – cos2 A = sin2)
⇒ cos2 A = sin4 A (Squaring both sides)
⇒ 1 – sin2 A = sin4 A
⇒ sin4 A + sin2 A = 1
49.
(a) sec A + tan A
(b) sec A – tan A
(c) sec A tan A
(d) none of these
Solution

= 1/cos A – sin A/cos A
= sec A – tan A
50.
(a) cos sec A – cot A
(b) cos sec A – cot A
(c) cosec A cot A
(d) none of these
Solution
(b) cos sec A + cot A

= (1 – cos A)/sin A
= 1/sin A – cos A/sin A
= cosec A – cot A
51. If tan θ = a/b, then (cos θ + sin θ)/(cos θ – sin θ) = ?
(a) (a + b)/(a – b)
(b) (a + b)/(a - b)
(c) (b + a)/(b – a)
(d) (b – a) /(b + a)
Solution
(c) (b + a)/(b – a)
Given: tan θ = a/b
Now, (cos θ + sin θ)/(cos θ – sin θ)
= (1 + tan θ)/(1 – tan θ) [Dividing the numerator and denominator by cos θ ]
= (1 + a/b)/(1 – a/b)
= ((b + a)/b))/((b – a)/b)
= (b + a)/(b – a)
52. (cosec θ – cot θ)2 = ?
(a) (1 + cos θ)/(1 – cos θ)
(b) (1 – cos θ)/(1 + cos θ)
(c) (1 + sin θ)/(1 – sin θ)
(d) none of these
Solution
(b) (1 – cos θ)/(1 + cos θ)
(cosec θ – cot θ)2
= (1/sin θ - cos θ/sin θ)2
= ((1 – cos θ)/sin θ)2
= (1 – cos θ)2/(1 – cos2 θ)
= (1 – cos θ)2/(1 + cos θ)(1 – cos θ)
= (1 – cos θ)/(1 + cos θ)
53. (sec A + tan A)(1 – sin A) = ?
(a) sin A
(b) cos A
(c) sec A
(d) cosec A
Solution
(b) cos A
(sec A + tan A)(1 – sin A)
= (1/cos A + sin A/cos A)(1 – sin A)
= (1 – sin A)/cos A(1 – sin A)
= (1 – sin2 A)/cos A
= cos2 A/cos A
= cos A









