RS Aggarwal Solutions Chapter 13 Construction Exercise 13A Class 10 Maths

Chapter Name | RS Aggarwal Chapter 13 Construction |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 13A Solutions
1. Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that AP/AB = 3/5.
Solution
Steps of Construction:
Step 1: Draw a line segment AB = 7 cm
Step 2: Draw a ray AX, making an acute angle ∠BAX.
Step 3: Along AX, mark 5 points (greater of 3 and 5) A1, A2, A3, A4 and A5 such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5
Step 4: Join A5B.
Step 5: From A3, draw A3P parallel to A5B (draw an angle equal to ∠AA5B), meeting AB in P.

2. Draw a line segment of length 7.6 cm and divide it in the ration 5: 8. Measure the two parts.
Solution
Steps of Construction:
Step 1: Draw a line segment AB = 7.6 cm
Step 2: Draw a ray AX, making an acute angle ∠BAX.
Step 3: Along AX, mark (5 + 8 = 13) points A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12 and A13 such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A6A7 = A8A9 = A9A10 = A10A11 = A11A12 – A12A13.
Step 4: Join A13B.
Step 5: From A5, draw A5P parallel to A13B (draw an angle equal to ∠AA13B), meeting AB in P.

∴ Length of AP = 2.9 cm (Approx)
Length of BP = 4.7 cm (Approx)
3. Construct a ΔPQR, in which PQ = 6 cm, QR = 7 cm and PR = -8 cm. Then, construct another triangle whose sides are 4/5 times the corresponding sides of ΔPQR.
Solution
Steps of Construction
Step 1: Draw a line segment QR = 7 cm.
Step 2: With Q as center and radius 6 cm, draw an arc.
Step 3: With R as center and radius 8 cm, draw an arc cutting the previous arc at P
Step 4: Join PQ and PR. Thus, ΔPQR is the required triangle.
Step 5: Below QR, draw an acute angle ∠RQX.
Step 6: Along OX, mark five points R1, R2, R3, R4 and R5 such that
QR1 = R1R2 = R2R3 = R3R4 = R4R5.
Step 7: Join RR5
Step 8: From R4, draw R4R’ ∥ RR5 meeting QR at R’.
Step 9: From R’, draw P’R’ ∥ PR meeting QR at R’.
Here, ΔP’QR’ is the required triangle, each of whose sides are 4/5 times the corresponding sides of ΔPQR.
4. Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle.
Solution
Steps of construction:
Step 1: Draw a line segment BC = 4 cm.
Step 2: With B as center, draw an angle of 90°.
Step 3: With B as center and radius equal to 3 cm, cut an arc at the right angle and name it A.
Step 4: Join AB and AC.
Thus, ΔABC is obtained.
Step 5: Extend BC to D, such that BD = 7/5.BC = 75(4) cm = 5.6 cm
Step 6: Draw DE ∥ CA, cutting AB produced to E.

Thus, ΔEBD is the required triangle, each of whose sides is 7/5 the corresponding sides of ΔABC.
5. Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are 3/4 times the corresponding sides of ΔABC.
Solution
Steps of construction
Step 1: Draw a line segment BC = 7 cm
Step 2: At B, draw ∠XBC = 60°.
Step 3: With B as center and radius 6 cm, draw an arc cutting the ray BX at A.
Step 4: Join AC, Thus, ΔABC is the required triangle.
Step 5: Below BC, draw an acute angle ∠YBC.
Step 6: Along BY, mark four points B1, B2, B3 and B4 such that BB1 = B1B2 = B2B3 = B3B4.
Step 7: Join CB4.
Step 8: From B, draw B3C’ ∥ CB4 meeting BC at C’’.
Step 9: From C’, Draw A’C’ ∥ AC meeting AB in A’.

Here, ΔA’BC’ is the required triangle whose sides are 3/4 times the corresponding sides of ΔABC.
6. Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠AB = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Solution
Steps of Construction
Step 1: Draw a line segment AB = 6 cm
Step 2: At A, draw ∠XAB = 30°.
Step 3: At B, draw ∠YBA = 60°. Suppose AX and BY intersect at C.
Thus, ΔABC is the required triangle.
Step 4: Produce AB to B’ such that AB’ = 8 cm
Step 5: From B’, draw B’C’ ∥ BC meeting AX at C’.

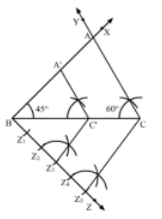
Solution
Steps of Construction:
Step 1: Draw a line segment BC = 8 cm.
Step 2: At B, draw ∠XBC = 45°.
Step 3: At C, draw ∠YCB = 60°. Suppose BX and CY intersect at A.
Thus, ΔABC is the required triangle.
Step 4: Below BC, draw an acute angle ∠ZBC.
Step 5: Along BZ, mark five points Z1, Z2, Z3, Z4 and Z5 such that
BZ1 = Z1Z2 = Z2Z3 = Z3Z4 = Z4Z5.
Step 6: Join CZ5.
Step 7: From Z3, draw Z3C’ ∥ CZ5 meeting BC at C’.
Step 8: From C’, draw A’C ∥ AC meeting AB in A’.
8. To construct a triangle similar to ΔABC in which BC = 4.5 cm, ∠B = 45° and ∠C = 60°, using a scale factor of 3/7, BC will be divided in the ratio
(a) 3 : 4
(b) 4 : 7
(c) 3 : 10
(d) 3 : 7
Solution
(a) 3 : 4
To construct a triangle similar to ΔABC in which BC = 4.5 cm, ∠B = 45° and ∠C = 60°, using a scale factor of 3/7, BC will be divided in the ratio 3 : 4.

Here, ΔABC ∼ ΔA’BC’
BC’: C’C = 3 : 4
Or BC’: BC = 3 : 7
Hence, the correct answer is option A.
9. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1.1/2 times the corresponding sides of the isosceles triangle.
Solution
Steps of Construction:
Step 1: Draw a line segment BC = 8 cm.
Step 2: Draw the perpendicular bisector XY to BC, cutting BC at D.
Step 3: With D as center and radius 4 cm, draw an arc cutting XT at A.
Step 4: Join AB and AC. Thus, an isosceles ΔABC whose base is 8 cm and altitude 4 cm is obtained.
Step 5: Extend BC to E such that BE = 3/2 BC = 3/2 × 8 cm = 12 cm
Step 6: Draw EF ∥ CA, cutting BA produced in F.

Here, ΔBEF is the required triangle similar to ΔABC such that each side of ΔBEF is 1.1/2 (or 3/2) times the corresponding side of ΔABC.
10. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm, Then, Construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Solution
Steps of Construction
Step 1: Draw a line segment BC = 3 cm.
Step 2: At B, draw ∠XBC = 90°.
Step 3: With B as center and radius 4 cm, draw an arc cutting BX at A.
Step 4: Join AC. Thus, a right ΔABC is obtained.
Step 5: Extend BC to D such that BD = 5/3 BC = 5/3 × 3 cm = 5 cm.
Step 6: Draw a DE ∥ CA, cutting BX in E.

