RS Aggarwal Solutions Chapter 12 Circles MCQ Class 10 Maths

Chapter Name | RS Aggarwal Chapter 12 Circles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Multiple Choice Questions
1. The number of tangents that can be drawn from an external point to a circle is
(a) 1
(b) 2
(c) 3
(d) 4
Solution
(b) 2
We can draw only two tangents from an external point to a circle.

2. In the given figure, RQ is a tangent to the circle with centre O, If SQ = 6 cm and QR = 4 cm, then OR is equal to

(b) 3 cm
(c) 5 cm
(d) 8 cm
Solution
We know that the radius and tangent are perpendicular at their point of contact OQ = 1/2QS = 3 cm [∵ Radius is half of diameter]
Now, in right triangle OQR
By using Pythagoras theorem, we have
OR2 = RQ2 + OQ2
= 42 + 32
= 16 + 9
= 25
∴ OR2 = 25
⇒ OR = 5 cm
3. If a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If O is the centre of the circle, then length OP = ?

(b) 28 cm
(c) 25 cm
(d) 18 cm
Solution
(c) 25 cm
The tangent at any point of a circle is perpendicular to the radius at the point of contact
∴ OT ⊥ PT
From right-angled triangle PTO,
∴ OP2 = OT2 + PT2 [Using Pythagoras’ theorem]
⇒ OP2 = (7)2 + (24)2
⇒ OP2 = 49 + 576
⇒ OP2 = 625

4. Which of the following pairs of lines in a circle cannot be parallel ?
(a) two chords
(b) a chord and tangent
(c) two tangents
(d) two diameters
Solution
Two diameters cannot be parallel as they perpendicular bisect each other.
5. The chord of a circle of radius 10 cm subtends a right angle at its centre. The length of the chord (in cm) is
(a) 5/√2
(b) 5√2
(c) 10√2
(d) 10√3
Solution
(c) 10√2

In right triangle AOB
By using Pythagoras theorem, we have
AB2 = BO2 + OA2
= 102 + 102
= 100 + 100
= 200
∴ OR2 = 200
⇒ OR = 10√2 cm
6. In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm, then the length of tangent PT is

(b) 10 cm
(c) 12 cm
(d) 16 cm
Solution
(a) 8 cm
In right triangle PTO
By using Pythagoras theorem, we have
PO2 = OT2 + TP2
⇒ 102 = 62 + TP2
⇒ 100 = 36 + TP2
⇒ TP2 = 64
⇒ TP = 8 cm
7. In the given figure, point P is 26 cm away from the center O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then, the radius of the circle is

(b) 12 cm
(c) 13 cm
(d) 15 cm
Solution
(a) 10 cm
Construction: Join OT.

We know that the radius and tangent are perpendicular at their point of contact
In right triangle PTO
By using Pythagoras theorem, we have
PO2 = OT2 + TP2
⇒ 262 = OT2 + 242
⇒ 676 = OT2 + 576
⇒ TP2 = 100
⇒ TP = 10 cm
8. PQ is a tangent to a circle with centre O at the point P. If ∆OPQ is an isosceles triangle, then ∠OQP is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution
(b) 45°

We know that the radius and tangent are perpendicular at their point of contact
Now, In isosceles right triangle POQ
∠POQ + ∠OPQ + ∠OQP = 180° [Angle sum property of a triangle]
⇒ 2∠OQP + 90° = 180°
⇒ ∠OQP = 45°
9. In the given figure, AB and AC are tangents to the circle with center O such that ∠BAC = 40°.Then, ∠BOC = 40°.

(b) 100°
(c) 120°
(d) 140°
Solution
(d) 140°
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBA = ∠OCA = 90°
Now, In quadrilateral ABOC
∠BAC + ∠OCA + ∠OBA + ∠BOC = 360° [Angle sum property of quadrilateral]
⇒ 40° + 90° + 90° + ∠BOC = 360°
⇒ 220° + ∠BOC = 360°
⇒ ∠BOC = 140°
10. If a chord AB subtends an angle of 60° at the center of a circle, then the angle between the tangents to the circle drawn from A and B is
(a) 30°
(b) 60°
(c) 90°
(d) 120°
Solution

We know that the radius and tangents are perpendicular at their point of contact
∵ ∠OBC = ∠OAC = 90°
Now, In quadrilateral ABOC
∠ACB + ∠OAC + ∠OBC + ∠AOB = 360° [Angle sum property of a quadrilateral]
⇒ ∠ACB + 90° + 90° + 60° = 360°
⇒ ∠ACB + 240° = 360°
⇒ ∠ACB = 120°
11. In the given figure, O is the centre of two concentric circles of radii 6 cm and 10 cm. AB is a chord of outer circle which touches the inner circle. The length of chord AB is

(b) 14 cm
(c) 16 cm
(d) √136 cm
Solution
(c) 16 cm
We know that the radius and tangent are perpendicular at their point of contact
In right triangle AOP
AO2 = OP2 + PA2
⇒ 102 = 62 + PA2
⇒ PA2 = 64
⇒ PA = 8 cm
Since, the perpendicular drawn from the center bisect the chord
∴ PA = PB = 8 cm
Now, AB = AP + PB = 8 + 8
= 16 cm
12. In the given figure, AB and AC are tangents to a circle with centre O and radius 8 cm. If OA = 17 cm, then the length of AC (in cm) is
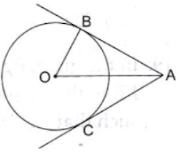
(b) 15
(c) √353
Solution
(b) 15
We know that the radius and tangent are perpendicular at their point of contact
In right triangle AOB
By using Pythagoras theorem, we have
OA2 = AB2 + OB2
⇒ 172 = AB2 + 82
⇒ 289 = AB2 + 64
⇒ AB2 = 225
⇒ AB = 15 cm
The tangents drawn from the external point are equal
Therefore, the length of AC is 15 cm
13. In the given figure, O is the centre of a circle, AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at the point A, then ∠BAT = ?

(b) 50°
(c) 60°
(d) 65°
Solution
(b) 50°
∠ABC = 90° (Angle in a semicircle)
In ΔABC, we have: ∠ACB + ∠CAB + ∠ABC = 180°
⇒ 50° + ∠CAB + 90° = 180°
⇒ ∠CAB = (180° - 140°)
⇒ ∠CAB = 40°
Now, ∠CAT = 90° (Tangents drawn from an external point are perpendicular to the radius at the point of contact)
∴ ∠CAB + ∠BAT = 90°
⇒ 40° + ∠BAT = 90°
⇒ ∠BAT = (90° - 40°)
⇒ ∠BAT = 50°
14. In the given figure, O is the center of a circle, PQ is a chord and Pt is the tangent at P. If ∠POQ = 70°, then ∠TPQ is equal to
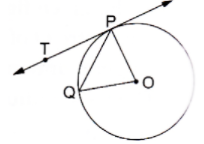
(b) 45°
(c) 55°
(d) 70°
Solution
(a) 35°
We know that the radius and tangent are perpendicular at their point of contact
Since, OP = OQ
∵ POQ is a isosceles right triangle
Now, In isosceles right triangle POQ
∠POQ + ∠OPQ + ∠OQP = 180° [Angle sum proper of a triangle]
⇒ 70° + 2∠OPQ = 180°
⇒ ∠OPQ = 55°
Now, ∠TPQ + ∠OPQ = 90°
⇒ ∠TPQ = 35°
15. In the given figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°, Then, AT = ?

(b) 2 cm
(c) 2√3 cm
(d) 4√3 cm
Solution
(c) 2√3 cm
OA ⊥ AT
So, AT/OT = cos 30°
⇒ AT/4 = √3/2
⇒ AT = (√3/2 × 4)
⇒ AT = 2√3
16. If PA and PB are two tangents to a circle with centre O such that ∠AOB = 110° then ∠APB is equal to

(b) 60°
(c) 70°
(d) 90°
Solution
(c) 70°
Given, PA and PB are tangents to a circle with center O, with ∠AOB = 110°.
Now, we know that tangents drawn from an external point are perpendicular to the radius at the point of contact.
So, ∠OAP = 90° and ∠OBP = 90°
⇒ ∠OAP + ∠OBP = 90° + 90° = 180°, which shows that OABP is a cyclic quadrilateral.
∴ ∠AOB + ∠APB = 180°
⇒ 110° + ∠APB = 180°
⇒ ∠APB = 180° - 110°
⇒ ∠APB = 70°
17. In the given figure, the length of BC is

(b) 10 cm
(c) 14 cm
(d) 15 cm
Solution
(b) 10 cm
We know that tangent segments to a circle from the same external point are congruent
Therefore, we have
AF = AE = 4 cm
BF = BD = 3 cm
EC = AC – AE = 11 – 4 = 7 cm
CD = CE = 7 cm
∴ BC = BD + DC = 3 + 7 = 10 cm
18. In the given figure, If ∠AOD = 135° then ∠BOC equal to

(b) 45°
(c) 52.5°
(d) 62.5°
Solution
(b) 45°
We know that the sum of angles subtended by opposite sides of a quadrilateral having a circumscribed circle is 180°
∴ ∠AOD + ∠BOC = 180°
⇒ ∠BOC = 180° - 135° = 45°
19. In the given figure, O is the centre of a circle and PT is the tangent to the circle. If PQ is a chord such that ∠QPT = 50° then ∠POQ = ?

(b) 90°
(c) 80°
(d) 75°
Solution
(a) 100°
Given, ∠QPT = 50°
And ∠OPT = 90° (Tangents drawn from an external point are perpendicular to the radius at the point of contact)
∴ ∠OPQ = (∠OPT - ∠QPT) = (90° - 50°) = 40°
OP = OQ (Radius of the same circle)
⇒ ∠OQP = ∠OPQ = 40°
In ΔPOQ, ∠POQ + ∠OQP + ∠OPQ = 180°
∴ ∠POQ = 180° - (40° + 40°) = 100°
20. In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then ∠OAB is

(b) 30°
(c) 60°
(d) 90°
Solution
(b) 30°
Construction: Join OB

We know that the radius and tangent are perpendicular at the point of contact
∴ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 60° + 90° = 360°
⇒ 240° + ∠AOB = 360°
⇒ ∠AOB = 120°
Now, In isosceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180° [Angle sum property of a triangle]
⇒ 120° + 2∠OAB = 180° [∵ ∠OAB = ∠OBA]
⇒ ∠OAB = 30°
21. If two tangents inclined at an angle of 60° are drawn to a circle of a radius 3 cm then the length of each tangent is
(a) 3 cm
(b) (3√3)/2 cm
(c) 3√3 cm
(d) 6 cm
Solution
(c) 3√3 cm
Given, PA and PB are tangents to circle with center O and radius 3 cm and ∠APB = 60°.
Tangents drawn from an external point are equal; so, PA = PB
And OP is the bisector of ∠APB, which gives ∠OPB = OPA = 30°.
OA ⊥ PA. So, from right -angled ΔOPA, we have:
OA/AP = tan 30°
⇒ OA/AP = 1/√3
⇒ 3/AP = 1/√3
= AP = 3√3 cm
22. In the given figure, PQ and PR are tangents to a circle with centre A. If ∠QPA = 27° then ∠QAR equals

(b) 117°
(c) 126°
(d) 153°
Solution
We know that the radius and tangent are perpendicular at the point of contact
Now, In ΔPQA
∠PQA + ∠QAP + ∠APQ = 180° [Angle sum property of a triangle]
⇒ 90° + ∠QAP + 27° = 180° [∵ ∠OAB = ∠OBA]
⇒ ∠QAP = 63°
In ΔPQA and ΔPRA
PQ = PR (Tangents draw from same external point are equal)
QA = RA (Ratio of the circle)
AP = AP (common)
By SSS congruency
ΔPQA ≅ PRA
∠QAP = ∠RAP = 63°
∴ ∠QAR = ∠QAP + ∠RAP = 63° + 63° = 126°
23. In the given figure, PQ and PR are tangents to a circle with centre A. If ∠QPA = 27° then ∠QAR equals

(b) 117°
(c) 126°
(d) 153°
Solution
(b) 117°
Construction: Join CA and CB

∵ ∠CAP = ∠CBP = 90°
Since, in quadrilateral ACBP all the angles are right angles
∴ ACPB is a rectangle
Now, we know that the pair of opposite sides are equal in rectangle
∴ CB = AP and CA = BP
Therefore, CB = AP = 4 cm and CA = BP = 4 cm
24. If PA and PB are two tangents to a circle with centre O such that ∠APB = 80°. Then,
∠AOP = ?

(b) 50°
(c) 60°
(d) 70°
Solution
(b) 50°
Given, PA and PB are two tangents to a circle with center O and ∠APB = 80°
∴ ∠APO = 1/2∠APB = 40°
[Since they are equally inclined to the line segment joining the center to that point and ∠OAP = 90°]
[Since tangents drawn from an external point are perpendicular to the radius at the point of contact]
Now, in triangle AOP:
∠AOP + ∠OAP + ∠APO = 180°
⇒ ∠AOP + 90° + 40° = 180°
⇒ ∠AOP = 180° - 130°
⇒ ∠AOP = 50°
25. In the given figure, O is the centre of the circle. AB is the tangent to the circle at the point P. If ∠APQ = 58° then the measure of ∠PQB is

(b) 58°
(c) 122°
(d) 132°
Solution
(a) 32°
We know that a chord passing through the center is the diameter of the circle.
∵ ∠QPR = 90° (Angle in a semi circle is 90°)
By using alternate segment theorem
We have ∠APQ = ∠PRQ = 58°
Now, In ΔPQR
∠PQR + ∠PRQ + ∠QPR = 180° [Angle sum property of a triangle]
⇒ ∠PQR + 58° + 90° = 180°
⇒ ∠PQR = 32°
26. In the given figure, O is the centre of the circle. AB is the tangent to the circle at the point P. If ∠PAO = 30° then ∠CPB + ∠ACP is equal to

(b) 90°
(c) 120°
(d) 150°
Solution
(b) 90°
We know that a chord passing through the center is the diameter of the circle.
∵ ∠DPC = 90° (Angle in a semicircle is 90°)
Now, In ΔCDP
∠CDP + ∠DCP + ∠DPC = 180° [Angle sum property of a triangle]
⇒ ∠CDP + ∠DCP + 90° = 180°
⇒ ∠CDP + ∠DCP = 90°
By using alternate segment theorem
We have ∠CDP = ∠CPB
∴ ∠CPB + ∠ACP = 90°
27. In the given figure, PQ is a tangent to a circle with centre O, A is the point of contact. If ∠PAB = 67°, then the measure of ∠AQB is
(a) 73°
(b) 64°
(c) 53°
(d) 44°

(d) 44°
We know that a chord passing through the center is the diameter of the circle.
∵ BAC = 90° (Angle in a semicircle is 90°)
By using alternate segment theorem
We have ∠PAB = ∠ACB = 67°
Now, In ABC
∠ABC + ∠ACB + ∠BAC = 180° [Angle sum property of a triangle]
⇒ ∠ABC + 67° + 90° = 180°
⇒ ∠ABC = 23°
Now, ∠BAQ = 180° - ∠PAB [Linear pair angles]
= 180° - 67°
= 113°
Now, In ΔABQ
∠ABQ + ∠AQB + ∠BAQ = 180° [Angle sum property of a triangle]
⇒ 23°+ ∠AQB + 113° = 180°
⇒ ∠AQB = 44°
28. In the given figure, two circles touch each other at C and AB is a tangent to both the circles. The measure of ∠ACB is

Solution
(c) 90°

We know that tangent segments to a circle from the same external point are congruent
Therefore, we have
NA = NC and NC = NB
We also know that angle opposite to equal sides is equal
∴ ∠NAC = ∠NCA and ∠NBC = ∠NCB
Now, ∠ANC + ∠BNC = 180° [Linear pair angles]
⇒ ∠NBC + ∠NCB + ∠NAC + ∠NCA = 180° [Exterior angle property]
⇒ 2∠NCB + 2∠NCA = 180°
⇒ 2(∠NCA + ∠NCA) = 180°
⇒ ∠ACB = 90°
29. O is the centre of a circle of radius 5 cm. At a distance of 13 cm from O, a point P is taken. From this point, two tangents PQ and PR are drawn to the circle. Then, the area of quad. PQOR is

(b) 32.5 cm2
(c) 65 cm2
(d) 30 cm2
Solution
(a) 60 cm2
Given,
OQ = OR = 5 cm, OP = 13 cm
∠OQP = ∠ORP = 90° (Tangents drawn from an external point are perpendicular to the radius at the point of contract)
From right-angled ΔPOQ:
PQ2 = (OP2 – OQ2)
⇒ PQ2 = (OP2 – OQ2)
⇒ PQ2 = 132 – 52
⇒ PQ2 = 169 – 25
⇒ PQ = 144

⇒ PQ = 12 cm
∴ ar(ΔOQP) = 1/2 × PQ × OQ
⇒ ar(ΔOQP) = (1/2 × 12 × 5) cm2
⇒ ar(ΔOQP) = 30 cm2
Similarly, ar(ΔORP) = 30 cm2
∴ ar(quad. PQOR) = (30 + 30) cm2
= 60 cm2
30. In the given figure, PQR is a tangent to the circle at Q, whose centre is O and AB is a chord parallel to PR such that ∠BQR = 70°. Then, ∠AQB = ?
(a) 20°
(b) 35°
(c) 40°
(d) 45°

(c) 40°
Since, AB ∥ PR, BQ is transversal
∠BQR = ∠ABQ = 70° [Alternative angles]
OQ ⊥ PQR (Tangents drawn from an external point are perpendicular to the radius at the point of contract)
and AB ∥ PQR
∴ QL ⊥ AB; so, OL ⊥ AB
∴ OL bisects chord AB [Perpendicular drawn from the center bisects the chord]
From ΔQLA and QLB:
∠QLA = ∠QLB = 90°
LA = LB (OL bisects chord AB)
QL is the common side.
∴ ΔQLA ≅ QLB [By SAS congruency]
∴ ∠QAL = ∠QBL
⇒ ∠QAB = ∠QBA
∴ ΔAQB is isosceles
∴ ∠LQA = ∠LQR
∠LQP = ∠LQR = 90°
∠LQB = (90° - 70°) = 20°
∴ ∠LQA = ∠LQB = 20°
⇒ ∠LQA = ∠LQB = 20°
⇒ ∠AQB = ∠LQA + ∠LQB
= 40°
31. The length of the tangent from an external point P to a circle of radius 5 cm is 10 cm. The distance of the point from the centre of the circle is
(a) 8 cm
(b) √104 cm
(c) 12 cm
(d) √125 cm
Solution
(b) √125 cm
We know that the radius and tangent are perpendicular at their point of contact
In right triangle PTO
By using Pythagoras theorem, we have
PO2 = OT2 + TP2
⇒ PO2 = 52 + 102
⇒ PO2 = 25 + 100
⇒ PO2 = 125
32. In the given figure, O is the centre of a circle, BOA is its diameter and the tangent at the point P meets BA extend ay T. If ∠PBO = 30° then ∠PTA = ?

(b) 30°
(c) 15°
(d) 45°
Solution
(b) 30°
We know that a chord passing through the center is the diameter of the circle
∵ ∠BPA = 90° (Angle in a semicircle is 90°)
By using alternate segment theorem
We have ∠APT = ∠ABP = 30°
Now, In ΔABP
∠PBA + ∠BPA + ∠BPA = 180° [Angle sum property of a triangle]
⇒ 30° + 90° + ∠BAP = 180°
⇒ ∠BAP = 60°
Now, ∠BAP = ∠APT + ∠PTA
⇒ 60° = 30° + ∠PTA
⇒ ∠PTA = 30°
33. In the given figure, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm then the perimeter of ΔEDF is

(b) 12 cm
(c) 13.5 cm
(d) 18 cm
Solution
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
EK = EM = 9 cm
Now, EK + EM = 18 cm
⇒ ED + DK + EF + FM = 18 cm
⇒ ED + DH + EF + HF = 18 cm (∵ DK = DH and FM = FH)
⇒ ED + DF + EF = 18 cm
⇒ Perimeter of ΔEDF = 18 cm
34. To draw a pair of tangents to a circle, which are inclined to each other at an angle of 45°, we have to draw tangents at the end points of those two radii, the angle between which is
(a) 105°
(b) 135°
(c) 140°
(d) 145°
Solution
(b) 135°

Suppose PA and PB are two tangents we want to draw which inclined at an angle of 45°
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBP = ∠OAP = 90°
Now, in quadrilateral AOBP
∠AOB + ∠OBP + ∠OAP + ∠APB = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 90° + 45° = 360°
⇒ ∠AOB + 225° = 360°
⇒ ∠AOB = 135°
35. In the given figure, O is the centre of a circle; PQL and PRM are the tangents at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and DE ⊥ DF OQ ⊥ BC and OR ⊥ AC. Then, ∠QSR = ?

(b) 50°
(c) 60°
(d) 70°
Solution
(d) 70°
PQL is a tangent OQ is the radius; so, ∠OQL = 90°
∴ ∠OQS = (90° - 50°) = 40°
Now, OQ = OS (Radius of the same circle)
⇒ ∠OSQ = ∠OQS = 40°
Similarly, ∠ORS = (90° - 60°) = 30°
And, OR = OS (Radius of the same circle)
⇒ ∠OSR = ∠ORS = 30°
∴ ∠QSR = ∠OSQ + ∠OSR
⇒ ∠QSR = (40° + 30°)
⇒ ∠QSR = 70°
36. In the given figure, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2 then the length of side of PQ is
(a) 17.5 cm
(b) 20 cm
(c) 22.5 cm
(d) 25 cm


We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
PS = PU = x
QT = QS = 12 cm
RT = RU = 9 cm
Now,
Ar(ΔPQR) = Ar(ΔPOR) + Ar(ΔQOR) + Ar(ΔPOQ)
⇒ 189 = 1/2 × OU × PR + 1/2 × OT × QR + 1/2 × OS × PQ
⇒ 378 = 6 × (x + 9) + 6 × (21) + 6 × (12 + x)
⇒ 63 = x + 9 + 21 + x + 12
⇒ 2x = 21
⇒ x = 10.5 cm
Now, PQ = QS + SP
= 12 + 10.5 + 10.5
= 22.5 cm
37. In the given figure, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm then the length of QR is

(b) 3.8 cm
(c) 5.7 cm
(d) 7.6 cm
Solution
(d) 7.6 cm
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
PT = PO = 3.8 cm and PT = PR = 3.8 cm
∴ QR = QP + PR = 3.8 + 3.8
= 7.6 cm
38. In the given figure, quad. ABCD is circumscribed touching the circle at P, Q, R and S. If AP = 5 cm, BC = 7 cm and CS = 3 cm. Then, the length of AB = ?

(b) 10 cm
(c) 12 cm
(d) 8 cm
Solution
(a) 9 cm
Tangents drawn from an external point to a circle are equal.
So, AQ = AP = 5 cm
CR = CS = 3 cm
And BR = (BC – CR)
⇒ BR = (7 – 3) cm
⇒ BR = 4 cm
BQ = BR = 4 cm
⇒ AB = (5 + 4) cm
⇒ AB = 9 cm
39. In the given figure, quad. ABCD is circumscribed, touching the circle at P, Q, R and S. If AP = 6 cm, BP = 5 cm, CQ = 3 cm and DR = 4 cm then perimeter of quad. ABCD is

(b) 27 cm
(c) 36 cm
(d) 32 cm
Solution
(c) 36 cm
Given, AP = 6 cm, BP = 5 cm, CQ = 3 cm and DR = 4 cm
Tangents drawn from an external point to a circle are equal
So, AP = AS = 6 cm, BP = BQ = 5 cm, CQ = CR = 3 cm, DR = DS = 4 cm.
∴ AB = AP + BP = 6 + 5 = 11 cm
BC = BQ + CQ = 5 + 3 = 8 cm
CD = CR + DR = 3 + 4 = 7 cm
AD = AS + DS = 6 + 4 = 10 cm
∴ Perimeter of quadrilateral ABCD = AB + BC + CD + DA
= (11 + 8 + 7 + 10) cm
= 36 cm
40. In the given figure, O is the centre of a circle, AB is a chord and AT is the tangent at A. If ∠AOB = 100° then ∠BAT is equal to

(b) 50°
(c) 90°
(d) 100°
Solution
(b) 50°
Given: AO and BC are the radius of the circle
Since, AO = BO
∴ ΔAOB is an isosceles triangle
Now, In ΔAOB
∠AOB + ∠OBA + ∠OAB = 180° (Angle sum property of triangle)
⇒ 100° + ∠OAB + ∠OAB = 180° (∠OBA = ∠OAB)
⇒ 2∠OAB = 80°
⇒ ∠OAB = 40°
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OAT = 90°
⇒ ∠OAB + ∠BAT = 90°
⇒ ∠BAT = 90° - 40 = 50°
41. In a right triangle ABC, right angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle is
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Solution
(b) 2 cm

In right triangle ABC
By using Pythagoras theorem we have
AC2 = AB2 + BC2
= 52 + 122
= 25 + 144
= 169
∴ AC2 = 169
⇒ AC = 13 cm
Now,
Ar(ΔABC) = Ar(ΔAOB) + Ar(ΔBOC) + Ar(ΔAOC)
⇒ 1/2 × AB × BC = 1/2 × OP × AB + 1/2 × OQ × BC + 1/2 × OR × AC
⇒ 5 × 12 = x × 5 + x × 12 + x × 13
⇒ 60 = 30x
⇒ x = 2 cm
42. In the given figure, a circle is inscribed in a quadrilateral ABCD touching its sides AB, BC, CD and AD at P, Q, R and S respectively. If the radius of the circle is 10 cm, BC = 38 cm, PB = 27 cm and AD ⊥ CD then the length of CD is

(b) 15 cm
(c) 20 cm
(d) 21 cm
Solution
(d) 21 cm
Construction: Join OR

We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
BP = BQ = 27 cm
CQ = CR
Now, BC = 38 cm
⇒ BQ + QC = 38
⇒ QC = 38 – 27 = 11 cm
Since, all the angles in quadrilateral DROS are right angles.
Hence, DROS is a rectangle.
We know that opposite sides of a rectangle are equal
∴ OS = RD = 10 cm
Now, CD = CR + RD
= CQ + RD
= 11 + 10
= 21 cm
43. In the given figure, ΔABC is right-angled at B such that BC = 6 cm and AB = 8 cm. A circle with center O has been inscribed the triangle. OP ⊥ AB, OQ ⊥ BC and OR ⊥ AC. If OP = OQ = OR = x cm then x = ?

(b) 2.5 cm
(c) 3 cm
(d) 3.5 cm
Solution
(a) 2 cm
Given, AB = 8 cm, BC = 6 cm
Now, in ΔABC:
AC2 = AB2 + BC2
⇒ AC2 = (82 + 62)
⇒ AC2 = (64 + 36)
⇒ AC2 = 100

⇒ AC = 10 cm
PBOQ is a square
CR = CQ (Since the lengths of tangents drawn from an external point are equal)
∴ CQ = (BC – BQ) = (6 – x) cm
Similarly, AR = AP = (AB = BP) = (8 – x) cm
∴ AC = (AR + CR) = [(8 – x) + (6 – x)] cm
⇒ 10 = (14 – 2x) cm
⇒ 2x = 4
⇒ x = 2 cm
∴ The radius of the circle is 2 cm.
44. Quadrilateral ABCD is circumscribed to a circle. If AB = 6 cm, BC = 7 cm and CD = 4 cm then the length of AD is
(a) 3 cm
(b) 4 cm
(c) 6 cm
(d) 7 cm
Solution
(a) 3 cm

We know that when a quadrilateral circumscribes a circle then sum of opposes sides is equal to sum of other opposite sides
∴ AB + DC = AD + BC
⇒ 6 + 4 = AD + 7
⇒ AD = 3 cm
45. In the given figure, PA and PB are tangents to the given circle such that PA = 5 cm and ∠APB = 60°. The length of chord AB is

Solution
(b) 5 cm
The lengths of tangents drawn from a point to a circle are equal
So, PA = PB and therefore, ∠PAB = ∠PBA = x (say).
Then, in ∆PAB:
∠PAB + ∠PBA + ∠APB = 180°
⇒ x + x + 60° = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = 60°
∴ Each angle of ∆PAB is 60°and therefore, it is an equilateral triangle.
∴ AB = PA = PB = 5 cm
∴ The length of the chord AB is 5 cm.
46. In the given figure, DE and DF are tangents from an external point D to a circle with centre A. If DE = 5 cm and DE ⊥ DF then the radius of the circle is
(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 6 cm
Solution
(c) 5 cm
Construction: Join AF and AE

We know that the radius and tangent are perpendicular at their point of contact
∵ ∠AED = ∠AFD = 90°
Since, in quadrilateral AEDF all the angles are right angles
∴ AEDF is a rectangle.
Now, we know that the pair of opposite sides is equal in rectangle
∴ AF = DE = 5 cm
Therefore, the radius of the circle is 5 cm.
47. In the given figure, three circles with centres A, B, C respectively touch each other externally. If AB = 5 cm, BC = 7 cm and CA = 6 cm then the radius of the circle with centre A is

Solution
(b) 2 cm
Given AB = 5 cm, BC = 7 cm and CA = 6 cm
Let, AR = AP = x cm
BQ = BP = y cm
CR = CQ = z cm
(Since the length of tangents drawn from an external point are equal)
Then, AB = 5 cm
⇒ AP + PB = 5 cm
⇒ x + y = 5 …(i)
Similarly, y + z = 7 …(ii)
And z + x = 6 …(iii)
Adding (i), (ii) and (iii), we get:
(x + y ) + (y + z) + (z + x) = 18
⇒ 2(x + y + z) = 18
⇒ (x + y + z) = 9 ….(iv)
Now, (iv) – (ii):
⇒ x = 2
∴ The radius of the circle with center A is 2 cm.
48. In the given figure, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm then the length of AP is
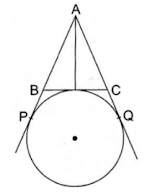
Solution
(d) 7.5 cm
We know that tangent segments to a circle from the same external point are congruent
Therefore, we have
AP = AQ
BP = BD
CQ = CD
Now, AB + BC + AC = 5 + 4 + 6 = 15
⇒ AB + BD + DC + AC = 15 cm
⇒ AB + BP + CQ + AC = 15 cm
⇒ AP + PQ = 15 cm
⇒ 2AP = 15 cm
⇒ AP = 7.5 cm
49. In the given figure, O is the centre of two concentric circles of radii 5 cm and 3 cm. From an external point P tangents PA and PB are drawn to these circles. If PA = 12 cm then PB is equal to

Solution
(c) 4√10 cm

Given, OP = 5 cm, PA = 12 cm
Now, Join O and B
Then, OB = 3 cm
Now, ∠OAP = 90° (Tangents drawn from an external point are perpendicular to the radius at the point of contact)
Now, in ΔOAP:
OP2 = OA2 + PA2
⇒ OP2 = 52 + 122
⇒ OP2 = 169

⇒ OP = 13
Now, in ΔOBP:
PB2 = OP2 – OB2
⇒ PB2 = 132 – 32
⇒ PB2 = 169 – 9
⇒ PB2 = 160

(a) If a point P lies inside a circle, not tangent can be drawn to the circle, passing through P.
(b) If a point P lies on the circle, then one and only one tangent can be drawn to the circle at P.
(c) If a point P lies outside the circle, then only two tangents can be drawn to the circle from P.
(d) A circle can have more than two parallel tangents, parallel to a given line.
Solution
(d) A circle can have more than two parallel tangents, parallel to a given line.
A circle can have more than two parallel tangents parallel to a given line. This statement is false because there can only be two parallel tangents to the given line in a circle.
51. Which of the following statements is not true?
(a) A tangent to a circle intersects the circle exactly at one point.
(b) The point common to the circle and its tangent is called the point of contact.
(c) The tangent at any point of a circle is perpendicular to the radius of the radius of the circle through the point of contact.
(d) A straight line can meet a circle at one point only.
Solution
(d) A straight line can meet a circle at one point only.
A straight be can meet a circle at one point only This statement is not true because a straight line that is not a tangent but a secant cuts the circle at two points.
52. Which of the following statement is not true ?
(a) A line which intersect a circle in two points, is called secant of the circle.
(b) A line intersecting a circle at one point only, is called a tangent to the circle.
(c) The point at which a line touches the circle, is called the point of contact.
(d) A tangent to the circle can be drawn from a point inside the circle.
Solution
(d) A tangent to the circle can be drawn from a point inside the circle.
This statement is false because tangents are the lines drawn from an external point to the circle that touch the circle at one point.
Assertion and Reason Type Questions Circles Class 10 Maths
Each question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
(c) Assertion (A) is true and Reason (R) is false.
(d) Assertion (A) is false and Reason (R) is true.
53.
|
The correct answer is (a) / (b) / (c) / (d).
(a) Both Assertion (A) and Reason (R) are true and reason (R) is a correct explanation of Assertion (A).

In ΔOPQ, ∠OPQ = 90°
∴ OQ2 = OP2 + PQ2
 54.
|
Solution
Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).
Assertion-
We know that If two tangents are drawn to a circle from an external pout, they subtend equal angles at the center.
Reason:

Given, a parallelogram ABCD circumscribes a circle with center O
AB = BC = CD = AD
We know that the tangents drawn from an external point to circle are equal
∴ AP = AS …(i) [tangents from A]
BP = BQ ….(ii) [tangents from B]
CR = CQ ….(iii) [tangents from C]
DR = DS …(iv) [tangents from D]
∴ AB + CD = AP + BP + CR + DR
= AS + BQ + CQ + DS [From (i). (ii), (iii) and (iv)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Thus, (AB + CD) = (AD + BC)
⇒ 2AB = 2AD [∵ Opposite sides of a parallelogram are equal]
⇒ AB = AD
∴ CD = AB = AD = BC
Hence, ABCD is a rhombus.
55.
Assertion (A) | Reason (R) |
In the given figure a quad. ABCD is drawn to circumscribe a given circle, as shown, Then, AB + BC = AD + DC  | In two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact. |
The correct answer is (a) / (b) / (c)/ (d).
Solution
(d) Assertion (A) is false and Reason (R) is true.
MCQ for Circles Class 10 Maths
1. In the given figure, O is the center of a circle. PQ is a chord and the tangent PT at P makes an angle of 50° with PQ. Then, ∠POQ = ?

(b) 100°
(c) 90°
(d) 75°
Solution
(b) 100°
Given, ∠QPT = 50°
Now, ∠OPT = 90° (Since tangents drawn from an external point are perpendicular to the radius at point of contact)
∴ ∠OPQ = (∠OPT - ∠QPT) = (90° - 50°) = 40°
OP = OQ (Radii of the same circle)
⇒ ∠OPQ = ∠OQP = 40°
In ΔPOQ
∠POQ + ∠OPQ + ∠OQP = 180°
⇒ ∠POQ + 40° + 40° = 180°
⇒ ∠POQ = 180° - (40° + 40°)
⇒ ∠POQ = 180° - 80°
⇒ ∠POQ = 100°
2. If the angles between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is
(a) 65°
(b) 40°
(c) 50°
(d) 90°
Solution
(c) 50°

OA and OB are the two radii of a circle with center O.
Also, AP and BP are the tangents to the circle.
Given, ∠AOB = 130°
Now, ∠OAB = ∠OBA = 90° (Since tangents drawn from an external point are perpendicular to the radius at point of contact)
In quadrilateral OAPB,
∠AOB + ∠OAB + ∠OBA + ∠APB = 360°
⇒ 130° + 90° + 90° + ∠APB = 360°
⇒ ∠APB = 360° - (130° + 90° + 90°)
⇒ ∠APB = 360° - 310°
⇒ ∠APB = 50°
3. If tangents PA and PB from a point P to a circle with center O are drawn so that ∠APB = 80, then, ∠POA ?

(b) 50°
(c) 80°
(d) 60°
Solution
(b) 50°
From ΔOPA and ΔOPB
OA = OB (Radii of the same circle)
OP (Common side)
PA = PB (Since tangents drawn from an external point to a circle are equal)
∴ ΔOPA ≅ ΔOPB (SSS rule)
∴ ∠APO = ∠BPO
∠APO = 1/2∠APB = 40°
And ∠OAP = 90° (Since tangents drawn from an external point are perpendicular to the radius at point of contact)
Now, in ΔOAP, ∠AOP + ∠OAP + ∠APO = 180°
⇒ ∠AOP + 90° + 40° = 180°
⇒ ∠AOP = 180° - 130° = 50°
4. In the given figure, AD and AE are the tangents to a circle with centre O and BC touches the circle at F. If AE = 5 cm, then perimeter of ΔABC is

(b) 10 cm
(c) 22.5 cm
(d) 20 cm
Solution
(b) 10 cm
Since the tangents from an external point are equal, we have
AD = AE, CD = CF, BE = BF
Perimeter of ΔABC = AC + AB + CB
= (AD – CD) + (CF + BF) + (AE – BE)
= (AD – CF) + (CF + BF) + (AE – BF)
= AD + AE
= 2 AE
= 2 × 5
= 10 cm
5. In the given figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

We know that tangent segments to a circle from the same external point are congruent
Now, we have
CR = CQ, AS = AP and BQ = BP
Now, BC = 7 cm
⇒ CQ + BQ = 7
⇒ BQ = 7 - CQ
⇒ BQ = 7 – 3 [∵ CQ = CR = 3]
⇒ BQ = 4 cm
Again, AB = AP + PB
= AP = BQ
= 5 + 4 [∵ AS = AP = 5]
= 9 cm
Hence, the value of x is 9 cm.
6. In the given figure, PA and PB are the tangents to a circle with centre O. Show that the points A, O, B, P are concyclic.

Here, OA = OB
And OA ⊥ AP, OA ⊥BP, (Since tangents drawn from an external point are perpendicular to the radius at the point of contact)
∴ ∠OAP = 90°, ∠OBP = 90°
∴ ∠OAP + OBP = 90° + 90° = 180°
∴ ∠AOB + ∠APB = 180° (Since, ∠OAP + ∠OBP + ∠AOB + ∠APB = 360°)
Sum of opposite angle of a quadrilateral is 180°.
Hence, A, O, B and P are concyclic.
7. In the given figure, PA and PB are two tangents form an externa point P to a circle with centre O. If ∠PBA = 65°, find the ∠OAB and ∠APB.

We know that tangents drawn from the external part are congruent
∴ PA = PB
Now, In isosceles triangle APB
∠APB + ∠PBA = ∠PAB = 180° [Angle sum property of a triangle]
⇒ ∠APB + 65° + 65° = 180° [∵ ∠PBA = ∠PAB = 65°]
⇒ ∠APB = 50°
We know that the radius and tangent are perpendicular at their port of contact
∴ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 50° + 90° = 360°
⇒ 230° + ∠BOC = 360°
⇒ ∠AOB = 130°
Now, In isosceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180° [Angle sum property of a triangle]
⇒ 130° + 2∠OAB = 180° [∵ ∠OAB = ∠OBA]
⇒ ∠OAB = 25°
8. Two tangents segments BC and BD are drawn to a circle with center O such that ∠CBD = 120°. Prove that OB = 2BC
Solution
Here, OB is the bisector of ∠CBD.
(Two tangents are equally inclined to the line segment joining the center to that point)
∴ ∠CBO = ∠DBO = 1/2∠CBD = 60°
∴ From ΔBOD, ∠BDO = 30°
Now, from right- angled ΔBOD,
⇒ BD/OB = sin 30°
⇒ OB = 2BD
⇒ OB = 2BC (Since tangents rom an external point are equal i.e., BC = BD)
∴ OB = 2BC
9. Fill in the blanks:
(i) A line intersecting a circle in two distinct point is called a ……
(ii) A circle can have two parallel tangents at the most ……
(iii) The common point of a tangents to a circle and the circle is called the …..
(iv) A circle can have …… tangents.
Solution
(i) A line intersecting a circle at two distinct points is called a secant.
(ii) A circle can have two parallel tangents at the most
(iii) The common point of a tangent to a circle and the circle is called the point of contact.
(iv) A circle can have infinite tangents.
10. Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Solution

To prove: AP = AQ
Join OP, OQ and OA.
AP is tangent at P and OP is the radius.
∴ OP ⊥ AP (Since tangents drawn from an external point are perpendicular to the radius at the point of contact)
Similarly, OQ ⊥ AQ
In the right ΔOPA and ΔOQA, we have:
OP = OQ [radii of the same circle]
∠OPA = ∠OQA = (90°)
OA = OA [Common side]
∴ ΔOPA ≅ ΔOQA [By R.H.S. – Congruence]
Hence, AP = AQ
11. Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
Solution

Now, radius of a circle is perpendicular to the tangent at the point of contact
∴ OA ⊥ AT and OB ⊥ BS (Since tangents drawn from an external point are perpendicular to the radius at point of contact)
∴ ∠OAT = ∠OBQ = 90°
But ∠OAT and ∠OBQ are alternate angles.
∴ AT is parallel to BS.
12. In the given figure, if AB = AC, prove that BE = CE.

Given: AB = AC
We know that the tangents from an external point are equal
∴ AD = AF, BD = BE and CF = CE ….(i)
Now, AB = AC
⇒ AD + DB = AF + FC
⇒ AF + DB = AF + FC [from (i)]
⇒ DB = FC
⇒ BE = CE [from (i)]
Hence proved.
13. If two tangents are drawn to a circle from an external point, show that they subtend equal angles at the centre.
Solution

To prove: ∠AOP = ∠AOQ
Proof: In ΔAOP = ΔAOQ, we have
AP = AQ [tangents from an external point are equal]
OP = OQ [radii of the same circle]
OA = OA [common side]
ΔAOP ≅ ΔAOQ [by SSS – congruence]
Hence, ∠AOP = ∠AOQ (c.p.c.t)
14. Prove that tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Solution
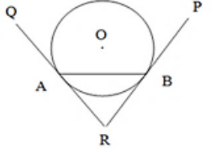
We have to prove that ∠RAB = ∠RDA.
∴ Now, RA = RB (Since tangents drawn from an external point to a circle are equal)
In ΔRAB, ∠RAB = ∠RDA (Since opposite sides are equal, their base angles are also equal)
15. Prove that the parallelogram circumscribing a circle, is a rhombus.
Solution

AB = BC = CD = AD
We know that the tangents drawn from an external point to circle are equal
∴ AP = AS ….(i) [tangents from A]
BP = BQ ….(ii) [tangents from B]
CR = CQ ….(iii) [tangents from C]
DR = DS …(iv) [tangents from D]
∴ AB + CD = AP + BP + CR + DR
= AS + BQ + CQ + DS [from (i), (ii), (iii) and (iv)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Thus, (AB + CD) = (AD + BC)
⇒ 2AB = 2AD [∵ Opposite sides of a parallelogram are equal]
⇒ AB = AD
∴ CD = AB = AD = BC
Hence, ABCD is a rhombus.
16. Two concentric circles are of radii 5 cm and 3 cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
Solution

In ΔOAC, OA2 = OC2 + AC2
∴ AC2 = OA2 – OC2
⇒ AC2 = 52 – 32
⇒ AC2 = 25 – 9
⇒ AC2 = 16
∴ AB = 2AC (Since perpendicular drawn from the center of the circle bisects the chord)
∴ AB = 2 × 4 = 8 cm
The length of the chord of the larger circle is 8 cm.
17. A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
Or
A quadrilateral is drawn to circumscribe a circle. Prove that the sum of opposite sides are equal.
Solution

∴ AP = AS …...(i) [tangents from A]
BP = BQ ….(ii) [tangents from B]
CR = CQ ….(iii) [tangents from C]
DR = DS ….(iv) [tangents from D]
∴ AB + CD = (AP + BP) + (CR + DR)
= (AS + BQ) + (CQ + DS) [using (i), (ii), (iii) and (iv)]
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence, (AB + CD) = (AD + BC)
18. Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution

To prove: ∠AOB + ∠COD = 180°
And ∠AOD + ∠BOC = 180°
Join: OP, OQ, OR and OS.
We know that the tangents drawn from an external point of a circle subtend equal angles at the center.
∴ ∠1 = ∠2 = ∠3, ∠4 = ∠5 and ∠6 = ∠8.
And ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360° [angles at a point]
⇒ (∠1 + ∠7) + (∠3 + ∠2) + (∠4 + ∠5) + (∠6 + ∠8) = 360°
2∠1 + 2∠2 + 2∠6 + 2∠5 = 360°
⇒ ∠1 + ∠2 + ∠5 + ∠6 = 180°
⇒ ∠AOB + ∠COD = 180° and ∠AOD + ∠BOC = 180°
19. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the segments joining the points of contact at the centre.
Solution

To prove: ∠APB + ∠AOB = 180°
We know that the tangent to a circle is perpendicular to the radius through the point of contact
∴ PA ⊥ OA
⇒ ∠OAP = 90°
PB ⊥ OB
⇒ ∠OBP = 90°
∴ ∠OAP + ∠OBP = (90° + 90°) = 180° …(i)
But we know that the sum of all the angles of a quadrilateral is 360°.
∴ ∠OAP + ∠OBP + ∠APB + ∠AOB = 360° …..(ii)
From (i) and (ii), we get:
∠APB + ∠AOB = 180°
20. PQ is a chord of length 16 cm of a circle of radius 10 cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.


We know that the perpendicular drawn from the center to the chord bisects it.
∴ PR = RQ
Now, PR + RQ = 16
PR + PR = 16
⇒ PR = 8
Now, in right triangle POR
By Using Pythagoras theorem, we have
PO2 = OR2 + PR2
⇒ 102 = OR2 + (8)2
⇒ OR2 = 36
Now, in right triangle TPR
By Using Pythagoras theorem, we have
TP2 = TR2 + PR2
⇒ x2 = y2 + (8)2
⇒ x2 = y2 + 64 ….(i)
Again, in right triangle TPQ
By Using Pythagoras theorem, we have
TO2 = TP2 + PO2
⇒ (y + 6)2 = x2 + 102
⇒ y2 + 12y + 36 = x2 + 100
⇒ y2 + 12y = x2 + 64 …..(2)
Solving (1) and (2), we get
x = 10.67
∴ TP = 10.67 cm
