RS Aggarwal Solutions Chapter 12 Circles Exercise 12B Class 10 Maths

Chapter Name | RS Aggarwal Chapter 12 Circles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 12B Solutions
1. In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.

We know that when a quadrilateral circumscribes a circle then sum of opposite sides is equal to the sum of other opposite sides.
∴ AB + CD = AD + BC
⇒ 6 + 8 = AD = 9
⇒ AD = 5 cm
2. In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

Construction: Join OB

We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 50° + 90° = 360°
⇒ 230° + ∠BOC = 360°
⇒ ∠AOB = 130°
Now, In isosceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180° [Angle sum property of a triangle]
⇒ 130° + 2∠OAB = 180° [∵ ∠OAB = ∠OBA]
⇒ ∠OAB = 25°
3. In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, find the ∠TRQ.

Construction: Join OQ and OT

We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OTP = ∠OQP = 90°
Now, In quadrilateral OQPT
∠QOT + ∠OTP + ∠OQP + ∠TPO = 360° [Angle sum property of a quadrilateral]
⇒ ∠QOT + 90° + 90° = 70° = 360°
⇒ 250° + ∠QOT = 360°
⇒ ∠QOT = 110°
We know that the angle subtended by an arc at the center is double the angle subtended by the arc at any point on the remaining part of the circle.
∴ ∠TRQ = 1/2(∠QOT) = 55°
4. In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB = CD.

We know that tangent segments to a circle from the same external point are congruent.
So, we have
EA = EC for the circle having center O1
and
ED = EB for the circle having centre O1
Now, Adding ED on both sides in EA = EC, we get
EA + ED = EC + ED
⇒ EA + EB = EC + ED
⇒ AB = CD
5. If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.

We know that the radius and tangent are perpendicular at their point of contact.
∴ ∠OPT = 90°
Now, ∠OPQ = ∠OPT - ∠TPQ = 90° - 70° = 20°
Since, OP = OQ as both are radius
∴ ∠OPQ = ∠OQP = 20° (Angles opposite to equal sides are equal)
Now,
In isosceles ∆POQ
∠POQ + OPQ + OQP = 180° (Angle sum property of a triangle)
⇒ ∠POQ = 180° - 20° = 140°
6. In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4 cm and 3 cm respectively. If the area of ∆ABC = 21 cm2 then find the lengths of sides AB and AC.

Construction: Join OA, OB, OC, OE ⊥ AB at E and OF ⊥ AC at F

We know that tangent segments to a circle from the same external point are congruent
Now, we have
AE = AF, BD = BE = 4 cm and CD = CF = 3 cm
Now,
Area (∆ABC) = Area(∆BOC) + Area(∆AOB) + Area (AOC)
⇒ 21 = 1/2 × BC × OD + 1/2 × AB × OE + 1/2 × AC × OF
⇒ 42 = 7 × 2 + (4 + x) × 2 + (3 + x) × 2
⇒ 21 = 7 + 4 + x + 3 + x
⇒ 21 = 14 + 2x
⇒ 2x = 7
⇒ x = 3.5 cm
∴ AB = 4 + 3.5 = 7.5 cm and AC = 3 + 3.5 = 6.5 cm
7. Two concentric circles are of radii5 cm and 3 cm. Find the length of the chord of the larger circle (in cm) which touches the smaller circle.
Solution

Given two circles have the same center O and AB is a chord of the larger circle touching the smaller circle at C; also, OA = 5 cm and OC = 3 cm
In ∆OAC, OA2 = OC2 + AC2
∴ AC2 = OA2 – OC2
⇒ AC2 = 52 – 32
⇒ AC2 = 25 – 9
⇒ AC2 = 16
⇒ AC = 4 cm
∴ AB = 2AC (Since perpendicular drawn from the center of the circle bisects the chord)
∴ AB = 2 × 4 = 8 cm
The length of the chord of the larger circle is 8 cm.
8. Prove that the perpendicular at the point of contact of the tangent to a circle passes through the centre.
Solution

To prove: PQ passes through the point O.
Construction: Join OP
Through O, draw a straight line CD parallel to the tangent AB.
Proof: Suppose that PQ doesn’t passes through point O.
PQ intersect CD at R and also intersect AB at P.
AS, CD ∥ AB. PQ is the line of intersection.
∠ORP = ∠RPA (Alternate interior angles) but also.
∠RPA = 90° (OP ⊥ AB)
⇒ ∠ORP = 90°
∠ROP + ∠OPA = 180° (Co-interior angles)
⇒ ∠ROP + 90° = 180°
⇒ ∠ROP = 90°
Thus, the ∆ORP has 2 right angles i.e., ∠ORP and ∠ROP which is not possible
Hence, our supposition is wrong
∴ PQ passes through the point O.
9. In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120°, then prove that OR = PR + RQ.


In ∆POR and ∆QOR
OP = OQ (Radii)
RP = RQ (Tangents from the external point are congruent).
OR = OR (Common)
By SSS congruency, ∆POR ≅ ∆QOR
∠PRO = ∠QRO (C.P.C.T)
Now, ∠PRO + ∠QRO = ∠PRQ
⇒ 2∠PRO = 120°
⇒ ∠PRO = 60°
Now, In ∆POR
cos 60° = PR/OR
⇒ 1/2 = PR/OR
⇒ OR = 2PR
⇒ OR = PR + PR
⇒ OR = PR + RQ
10. In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the length AD, BE and CF.

We know that segments to a circle from the same external point are congruent
Now, we have
AD = AF, BD = BE and CE = CF
Now, AD + BD = 14 cm ....(1)
AF + FC = 12 cm
⇒ AD + FC = 12 cm ...(2)
BE + EC = 8 cm
⇒ BD + FC = 8 cm ...(3)
Adding all these we get
AD + BD + AD + FC + BD + FC = 342
⇒ 2(AD + BD + FC) = 34
⇒ AD + BO + FC = 17 cm ...(4)
Solving (1) and (4), we get
FC = 3 cm
Solving (2) and (4), we get
BD = 5 cm = BE
Solving (3) and (4), we get
and AD = 9 cm
11. In the given figure, O is the centre of the circle, PA and PB are tangents. Show that AOBP is cyclic quadrilateral.
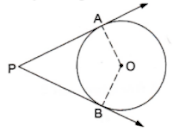
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠APB + ∠AOB + ∠OBP + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠APB + ∠AOB + 90° + 90° = 360°
⇒ ∠APB + ∠AOB = 180°
Since, the sum of the opposite angles of the quadrilateral is 180°
Hence, AOBP is a cyclic quadrilateral.
12. In two concentric circles. a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm then find the radius of the smaller circle.
Solution

Since, the perpendicular drawn from the centre bisect the chord
∴ AP = PB = AB/2 = 4 cm
In right triangle AOP
AO2 = OP2 + PA2
⇒ 52 = OP2 + 42
⇒ OP2 = 9
⇒ OP = 3 cm
Hence, the radius of the smaller circle is 3 cm.
13. In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If ∠QPT = 60°, find the ∠PRQ.

We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OPT = 90°
Now, ∠OPQ = ∠OPT - ∠QPT = 90° - 60° = 30°
Since, OP = OQ as born is radius
∴ ∠OPQ = ∠OQP = 30° (Angles opposite to equal sides are equal)
Now, In isosceles, POQ
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of a triangle)
⇒ POQ = 180° - 30° - 30° = 120°
Now, ∠POQ + reflex ∠POQ = 360° (Complete angle)
⇒ reflex ∠POQ = 360° - 120° = 240°
We know that the angle subtended by an arc at the centre double the angle subtended by the arc at any point on the remaining part of the circle.
∴ ∠PRQ = 1/2 (reflect ∠POQ) = 120°
14. In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60°, then find the measure of ∠AOB.

Construction: Join OB

∵ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 60° + 90° = 360°
⇒ 240° + ∠AOB = 360°
⇒ ∠AOB + 90° + 60° + 90° = 360°
⇒ 240° + ∠AOB = 360°
⇒ ∠AOB = 120°
Now, In isosceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180° [Angle sum property of a triangle]
⇒ 120° + 2∠OAB = 180° [∵ ∠OAB = ∠OBA]
⇒ ∠OAB = 30°
