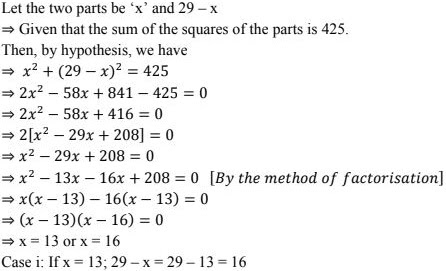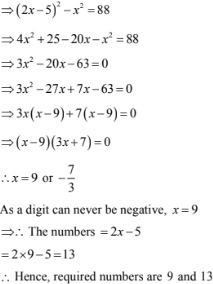RD Sharma Solutions for Class 10 Chapter 8 Quadratic Equations Exercise 8.7

RD Sharma Solutions Chapter 8 Quadratic Equations Exercise 8.7 Class 10 Maths

Chapter Name	RD Sharma Chapter 8 Quadratic Equations
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 8.1 Exercise 8.2 Exercise 8.3 Exercise 8.4 Exercise 8.5 Exercise 8.6 Exercise 8.8 Exercise 8.9 Exercise 8.10 Exercise 8.11 Exercise 8.12 Exercise 8.13
Related Study	NCERT Solutions for Class 10 Maths

Exercise 8.7 Solutions

1. Find the consecutive numbers whose squares have the sum 85. 

Solution

Let the two consecutive natural numbers be 'x' and 'x + 1'
Given that the sum of their squares is 85. 
Then by hypothesis, we get
x² + (x + 1)² = 85
⇒ x² + x² + 2x + 1 = 85 
⇒ 2x² + 2x + 1 - 85 = 0 
⇒ 2x² + 2x + 84 = 0 ⇒ 2[x² + x - 42] = 0 
⇒ x² + 7x - 6x - 42 = 0 [by the method of factorisation]
⇒ x(x + 7) - 6(x + 7) = 0 
⇒ (x - 6)(x + 7) = 0 
⇒  x = 6 or x = 7 
case i : if x = 6x + 1 = 6 + 1 = 7 
case ii: if x = 7x + 1 = - 7 + 1 = - 6 
∴ The consecutive numbers that the sum of this squares be 85 are 6, 7 and  -6, - 7.

2. Divide 29 into two parts so that the sum of the squares of the parts is 425. 

Solution

Case ii: x = 16; 29 - x = 29 - 16 = 13
∴ The two parts that the sum of the squares of the parts is 425 are 13, 16. 

3. Two squares have sides x cm and (x + 4)cm. The sum of this areas is 656 cm² . Find the sides of the squares. 

Solution 

The given sides of two squares = x cm and (x + 4)cm 
The sum of their areas  = 656 cm² . 
The area of the square = side × side 
∴ Area of the square = x(x + 4) cm² 
⇒ Given that sum of the areas is 656 cm² . 
Hence by hypothesis, we have 
⇒ x(x + 4) + x(x + 4) = 656 
⇒2x(x + 4) = 656 
⇒ x² + 4x = 328 [dividing both sides by 2]
⇒ x² + 4c - 328 = 0 
⇒ x² + 20x - 16x - 328 = 0 [∵ by the method of factorisation]
⇒ x(x + 20) - 16(x + 20) = 0 

⇒ (x + 20)(x - 16) = 0 ⇒ x = -20 or x = 16 
Case i: If x = 16; x + 4 = 20
∴ The sides of the squares are 16 cm and 20cm. 
Note : No negative value is considered as the sides will never be measured negatively. 

4. The sum of two numbers is 48 and their product is 432. Find the numbers 

Solution

Given the sum of two numbers is 48
Let the two numbers be x and 48 - x also given their product is 432. 
Hence x(48 - x) = 432 
⇒ 48x - x² = 432 
⇒ 48x - x² - 432 = 0 
⇒ x² - 48x + 432 = 0 
⇒ x² - 36x - 12x + 432 = 0  [By method of  factorisation] 
⇒ x(x - 36) - 12(x - 36) = 0 
⇒ (x - 36)(x - 12) = 0 
⇒ x = 36 or x = 12 
∴ The two numbers are 12, 36. 

5. If an integer is added to its square, the sum is 90. Find the integer with the help of quadratic equation. 

Solution

Let the integer be 'x'
Given that if an integer is added to its square, the sum is 90. 
⇒ x + x² = 90 
⇒ x + x² - 90 = 0 
⇒ x² + 10x - 9x - 90 = 0 
⇒ x(x + 10) - 9(x + 10) = 0 
⇒ x = - 10 or  x = 9 

∴ The value of an integer are -10 or 9.

6.  Find the whole numbers which when decrease by 20 is equal to 69 times the reciprocal of the members. 

Solution

Let the whole number be x as it is decreased by 20 ⇒ (x - 20) = 69.(1/2)

As the whole numbers are always positive, x = - 3 is not considered. 

∴ The whole number x = 23. 

7. Find the two consecutive natural numbers whose product is 20. 

Solution

Let the two consecutive natural numbers be 'x' and 'x + 2'
⇒ Given that the product of the natural numbers is 20 
Hence  ⇒ x(x + 1) = 20 
⇒ x² + x = 20 
⇒ x² + x - 20 = 0 
⇒ x² + 5x - 4x - 20 = 0 
⇒ x(x + 5) - 4(x + 5) = 0 
⇒ x = - 5 or x = 4 
Considering positive value of x as x ∈ N
For r = 4, x + 1 = 4 + 1 = 5 
∴ The two consecutive natural numbers are 4 as 5.

8. The sum of the squares of the two consecutive odd positive integers as 394. Find them. 

Solution

Let the consecutive odd positive integers are 2x - 1 and 2x + 1 
Given that the sum of the squares is 394. 
(2x - 1)² + (2x + 1)² = 394 
4x² + 1 - 4x + 4x² + 1 + 4x = 394 
8x² + 2 = 394 
4x² = 392
x² = 36 
x = 6 
As x = 6,
2x - 1  = 2×6 - 1 = 11 
2x + 1 = 2×6 + 1 = 13 
∴ The two consecutive odd positive numbers are 11 and 13.

9. The sum of two numbers is 8 and 15 times the sum of their reciprocals is also 8. Find the numbers. 

Solution

Let the numbers be x and 8 -x
Given that the sum of these numbers is 8
And 15 times the sum of their reciprocals as 8

10. The sum of a numbers and its positive square root is 6/25. Find the numbers. 

Solution

Let the number be x 
By the hypothesis we have 

⇒ x + √x = 6/25 

11. The sum of a number and its square is 63/4. Find the numbers. 

Solution

Let the number be x. 

Given that the sum of x and its square = 63/4

12. There are three consecutive integers such that the square of the first increased by the product of the first increased by the product of the others the two gives 154. What are the integers?

Solution

Let the three consecutive numbers x, x + 1 and x + 8. 

According to the hypothesis given 

13. The product of two successive integral multiples of 5 is  300. Determine the multiples. 

Solution

Given that the product of two successive integral multiples of 5 is 300. 
Let the integers be 5x, and 5(x + 1) 
Then, by the integers be 5x and 5(x + 1)
Then, by the hypothesis, we have 
5x . 5(x + 1) = 300 

14. The sum of the squares of two numbers as 233 and one of the numbers as 3 less than twice the other number find the numbers. 

Solution

Let the number be x 
Then the other number = 2x - 3 
According to the given hypothesis, 

15. Find the consecutive even integers whose squares have the sum 340. 

Solution

Let the consecutive even integers be 2x and 2x + 2.
Then according to the given hypothesis, 

16. The difference of two numbers is 4. If the difference of their reciprocals is 4/21. Find the numbers .

Solution

Let the two numbers be x and x - 4
Given that the difference of two numbers is 4. 
By the given hypothesis, we have 1/(x - 4) - 1/x = 4/21 

17. Let us find two natural numbers which differ by 3 and whose squares have the sum 117. 

Solution

Let the numbers be x and x = 3 
By the given hypothesis, 

18. The sum of the squares of three consecutive natural numbers as 149. Find the numbers.

Solution

19. Sum of two numbers is 16. The sum of their reciprocals is 1/3. Find the numbers. 

Solution

Given that the sum of two number is 16.

Let the two numbers be x and 16 -x 
By the given hypothesis, we have 

20. Determine two consecutive multiples of 3, whose product is 270.

Solution

Let the two consecutive multiples of 3 are 3x and 3x + 3 
Given that their product is 270 

21. The sum of a number and its reciprocal is 17/4. Find the number. 

Solution

Let the number be 'x'.
According to the given hypothesis

22. A two-digit number is such that the product of its digits is 8. When 18 is subtracted from the number, the digits interchange their places. Find the number ? 

Solution 
Let the two digits be x and x - 2 

Given that the product of their digits is  8. 

23. A two digits number is such that the product of the digits is 12. When 36 is added to the number, the digits inter change their places determine the number 

Solution

Let the tens digit be x 

24. A two digit number is such that the product of the digits is 16. When 54 is subtracted from the number the digits are interchanged. Find the number .

Solution

Let the two digits be: 

25. Two numbers differ by 3 and their product is 504. Find the number 

Solution

Let the two numbers be x and x - 3 given that x(x - 3) = 504 

26. Two number differ by  4 and their product is 192. Find the numbers ? 

Solution

Let the two numbers be x and x - 4 
Given that their product is 192 

27. A two - digit number is 4 times the sum of its digits and twice the product of its digits. Find the numbers. 

Solution

Let the digits at tens and units place of the number be x and y respectively then, it is 
given that  = 10x + y 
⇒ 10x + y = 4 (sum of digits) and 2xy
⇒ 10x + y = 4(x + y) and 10x + y = 3xy 
⇒ 10x + y = 4x + 4y and 10x + y = 3xy
⇒ 6x - 3y = 0 and 10x + y - 3xy = 0 
⇒ y = 2x and 10x + 2x = 2xy(2x)
⇒ 12x = 4x² 

⇒ 4x² - 12x = 0 
⇒ 4x(x - 3) = 0 
⇒ 4x = 0 or x = 3 
⇒ here we have y = 2x ⇒ 2×3 = 6
∴ x = 3 and y = 6 
Hence 10x + y = 10×3+6 = 36 
∴ The required two digit number is 36.

28. The sum of the squares of two positive integers is 208. If the square of the large number is 18 times the smaller. Find the numbers

Solution

Let the smaller number be x. Then square of a larger number = 18x 
Also, square of the smaller number = x² 
It is given that the sum of the square of the integers is 208.

But, the numbers are positive. Therefore x = 8 
∴ square of the larger number = 18x = 18 × 8 = 144 
⇒ larger number are 8 and  18.

29. The sum of two numbers is 18. The sum of their reciprocals is 1/4. Find the numbers 

Solution

Let the number be x and 18 - x 
⇒ according to the given hypothesis 

30. The sum of two numbers a and b is 15. And the sum of their reciprocals 1/a and 1/b is 3/10

Find the numbers a and b. 

Solution

Let us assume a number 'x'

∴ a = 5, b = 10 or a = 10 and b = 5 

31. The sum of two numbers is 9. The sum of their reciprocals is 1/2. Find the numbers. 

Solution

Given that the sum of two numbers is 9. Let the two numbers be x and 9 - x 
By the given hypothesis, we have 

32.  Three consecutive positive integers are such that the sum of the square of the first and the product of other two is 46. Find the integers. 

Solution

Let the three consecutive positive integers be x, x + 1 and x + 2 
According to the hypothesis, we have 

33. The difference of squares of two numbers is 88. If the larger number is 5 less than twice the smaller number, then find the two numbers. 

Solution

Let the smaller number be x. Then, larger number = 2x - 5 
It is given that the difference of the square of the number is 88. 

34. The difference of square of two numbers is 180, the square of the smaller number is 8 times the large numbers find two numbers. 

Solution

Let the number be x 
By the given hypothesis, we have 

Square of larger number 8x = - 80 here no perfect square exist, hence the numbers are 18, 12.