RD Sharma Solutions Chapter 5 Trigonometric Ratios Exercise 5.2 Class 10 Maths

RD Sharma Solutions Chapter 5 Trigonometric Ratios Exercise 5.2 Class 10 Maths

Chapter Name

RD Sharma Chapter 5 Trigonometric Ratios

Book Name

RD Sharma Mathematics for Class 10

Other Exercises

  • Exercise 5.1
  • Exercise 5.3

Related Study

NCERT Solutions for Class 10 Maths

Exercise 5.2 Solutions

Evaluate each of the following (1 - 19) :

1. sin 45° sin 30° + cos 45° cos30°

Solution 


2. Sin 60° cos 30° + cos 60° sin 30°

Solution 


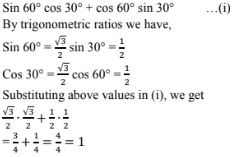
3. Cos 60° cos45° - sin 60°. sin 45°
Solution

4. sin2 30° + sin2 45° + sin2 60° + sin2 90°
Solution 

5. cos2 30° + cos2 45° + cos2 60° + cos2 90°
Solution 

6. tan2 30° + tan2 60° + tan2 45°
Solution 

7. 2sin2 30° - 3cos2 45° + tan2 60°
Solution 

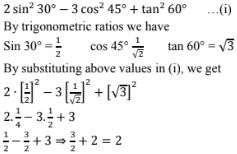
8. sin2 30° cos2 45° + 4tan2 30° + (1/2)sin2 90° - 2 cos2 90° + (1/24)cos2 0°
Solution 

9. 4(sin2 60° + cos4 30°) - 3(tan2 60° - tan2 45°) + 5cos2 45° 
Solution 

10. (cosec2 45° sec2 30°)(sin2 30° + 4 cot2 45° - sec2 60°) 
Solution 

11. cosec2 30° cos60° tan3 45° sin2 90° sec2 45° cot30°
Solution 

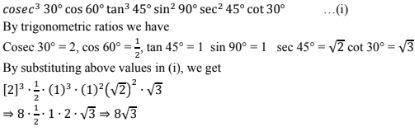
12. cot2 30° - 2cos2 60° - (3/4) sec2 45° - 4sec2 30°
Solution 

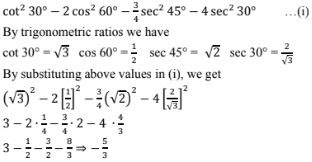
13. (cos0° + sin 45° + sin30°)(sin 90° - cos45° + cos60°) 
Solution 

14. (sin 30°- sin 90° + 2 cos 0°)/(tan° 30 tan 60°)
Solution 

15. 4/cot2 30° + 1/sin2 60° - cos2 45°
Solution 

16. 4(sin2 30° + cos2 60°) - 3(cos2 45° - sin2 90°) - sin2 60°
Solution 

17. (tan2 60° + 4cos2 45° + 3 sec2 30° + 5cos2 90°)/(cosec 30° + sec 60° - cot2 30°
Solution 

18. sin 30°/sin 45° + tan 45°/sec 60° - sin 60°/cot 45° - cos 30°/sin 90°
Solution 

19. tan 45°/cosec 30° + sec 60°/cot 45° - 5sin 90°/2cos 0° 
Solution 

20. 2sin 3x = √3 s = ? 
Solution 
Sin 3x = √3/2 
Sin 3x = sin 60°
Equating angles we get, 
3x = 60°
x = 20°

21. 2 sin x/2 = 1   x = ? 
Solution 
Sin x/2 = 1/2
Sin x/2 = sin 30°
x/2 = 30° 
x = 60°

22. √3 sin x = cos x 
Solution 
√3 tan x = 1 
tan x = 1/√3 
∴ tan x = tan 30°
x = 30°

23. tan x  = sin 45° cos 45° + sin 30° 
Solution 

24. √3 tan 2x = cos 60° + sin 45° cos 45°
Solution 

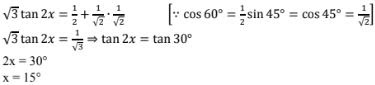
25. cos 2x = cos 60° cos 30° + sin 60° sin 30°
Solution 

26. If θ = 30° verify 
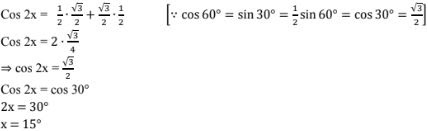
(i) tan 2θ = 2tanθ/(1 - tan2 Î¸)
Solution 
(i)

27. If A = B = 60°. Verify 
(i) cos(A - B) = cosA cosB + sin A + sin B
Solution 

28. If A = 30° B = 60° verify 
(i) sin (A + B) = sin A cos B + cos A sin B
Solution 

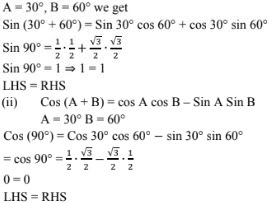
29. sin (A - B) = sin A cos B - cos A sin B 
cos (A - B) = cos A cos B - sin A sin B 
Find sin 15° cos 15°
Solution

30. In right angled triangle ABC. ∠C = 90°, ∠B = 60° . AB = 15 units. Find remaining angles and sides. 
Solution 

31. In ΔABC is a right triangle such that ∠C = 90° , ∠A = 45° ,  BC = 7 units find ∠B, AB and AC. 
Solution 

32. In rectangle ABCD AB = 20cm ∠BAC = 60° BC, calculate side BC and diagonals AC and BD. 
Solution 

33. If sin(A + B) = 1 and cos(A - B) = 1, 0° < A + B ≤ 90° A ≥ B. Fin A & B
Solution 

34. If tan(A - B) = 1/√3 and tan(A + B) = √3, 0° < A + B ≤ 90° , A ≥ B, Find A & B. 
Solution 

35. If sin(A - B) = 1/2 and cos(A +B) = 1/2, 0° < A + B ≤ 90° , A > B, Find A & B 
Solution 

36. In right angled triangle ΔABC at B, ∠A = ∠C. Find the values of 
(i) sin A cos C + cos A sin C 
Solution 

37. Find acute angles A & B, if sin (A + 2B) = √3/2 cos(A + 4B) = 0, A > B> 
Solution 

38.  If A and B are acute angles such that tan A = 1/2 , tan B = 1/3 and tan (A + B) = (tanA + tan B)/(1 - tan A tan B)  , A + B = ? 
Solution 

39. In ΔPQR, right angled at Q, PQ = 3cm PR = 6cm. Determine ∠P = ? ∠R = ? 
Solution 

Tags
Previous Post Next Post