RD Sharma Solutions for Class 10 Chapter 4 Triangles Exercise 4.5

RD Sharma Solutions Chapter 4 Triangles Exercise 4.5 Class 10 Maths

Chapter Name	RD Sharma Chapter 4 Triangles
Book Name	RD Sharma Mathematics for Class 10
Other Exercises	Exercise 4.1 Exercise 4.2 Exercise 4.3 Exercise 4.4 Exercise 4.6 Exercise 4.7
Related Study	NCERT Solutions for Class 10 Maths

Exercise 4.5 Solutions

1. In fig. 4.136, ΔACB ～ΔAPQ. If BC = 8cm, PQ = 4cm, BA = 6.5cm and AP = 2.8 cm, find CA and AQ. 

Solution

Given ΔACB ～ΔAPQ 

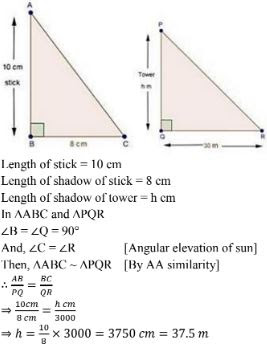
2. A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a shadow 30 m long. Determine the height of the tower. 

Solution

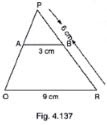
3. In Fig 4.137, AB||QR. Find the length of PB. 

Solution

We have, ΔPAB and ΔPQR 
∠P = ∠P  [common]
∠PAB = ∠PQR [corresponding angles] 
Then, ΔPAB～ΔPQR  [ By AA similarity] 

4. In fig. 4.138, XY ||BC. Find the length of XY 

Solution

We have, XY ||BC 
In ΔAXY and ΔABC 
∠A = ∠A  [common]
∠AXY = ∠ABC [corresponding angles]
Then, ΔAXY ～ ΔABC [By AA similarity]

5. In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx. 

Solution

We have ∠C = 90° and CD ⊥ AB 

6. In Fig. 4.139, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4cm, find CD. 

Solution

We have, ∠ABC = 90° and BD ⊥ AC 
Now, ∠ABD + ∠DBC - 90°  ...(i) [∵ ∠ABC - 90°] 
And ∠C + ∠DBC - 90° ...(ii) [By angle sum prop. in ΔBCD]
Compare equations (i) & (ii) 
∠ABD = ∠C ...(iii) 
In ΔABD and ΔBCD 
∠ABD = ∠C  [ From (iii)]
∠ADB = ∠BDC  [Each 90° ]
Then, ΔABD ～ΔBCD [By AA similarity]

7. In Fig. 4.14, ∠ABC = 90° and BD ⊥ AC. If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC. 

Solution

We have, ∠ABC = 90° and BD⊥ AC
In ΔABC and ΔBDC 
∠ABC = ∠BDC  [Each 90°]
∠C = ∠C [Common]
Then, ΔABC ～ ΔBDC  [By AA similarity] 

8. In Fig. 4.141, DE||BC such that AE = (1/4)AC. If AB = 6 cm, find AD. 

Solution

We have, DE||BC, AB = 6cm and AE = 1/4 AC
In ΔADE and ΔABC 
∠A = ∠A  [Common] 
∠ADE = ∠ABC [Corresponding angles]
Then, ΔADE ～ΔABC  [By AA similarity]

9. In fig., 4.142, PA, QB and RC are each perpendicular to AC. Prove that 1/x + 1/z + 1/y 

Solution

We have, PA ⊥ AC, QB ⊥ AC and RC⊥AC 
Let, AB = a and BC = b
In ΔCQB and ΔCPA 
∠QCB = ∠PCA  [Common] 
∠QBC = ∠PAC [Each 90°]
Then, ΔCQB ～ΔCPA  [By AA similarity] 

10. In below fig, ∠A = ∠CED, Prove that ΔCAB ～ΔCED. Also, find the value of x. 

Solution

11. The perimeters of two similar triangles are 25cm and 15cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle ? 

Solution

Assume ABC and PQR to be 2 triangles 
We have, 
ΔABC ～ ΔPQR 
Perimeter of ΔABC = 25cm 
Perimeter of ΔPQR = 15 cm 
AB = 9 cm 
PQ = ? 
Since, ΔABC ～ΔPQR 
Then, ratio of perimeter of triangles = ratio of corresponding sides 

12. In ΔABC and ΔDEf, it is being given that : AB = 5cm, BC = 4cm and CA = 4.2cm; 
DE = 10cm, EF = 8cm and FD = 8.4 cm, If AL  ⊥ BC and DM ⊥ EF, find AL: DM.

Solution

13. D and E are the points on the sides AB and AC respectively of a ΔABC such that ; Ad = 8cm, DB = 12cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.

Solution

14. D is the mid - point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1

Solution

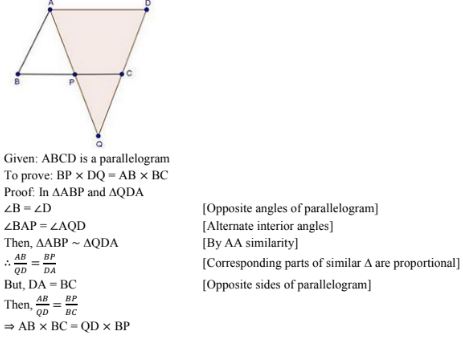
15.  ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the AB and BC. 

Solution

16. In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that : 
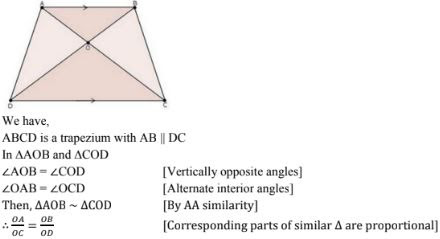
(i) ΔOMA and ΔOLC
(ii) OA/OC = OM/OL 

Solution

17. In Fig below we have AB || CD|| EF. If AB = 6 cm, Cd = x cm, EF = 10 cm, BD = 4 cm and DE = y cm, calculate the values of x and y . 

Solution

We have AB ||CD||EF. If AB = 6 cm, CD = x cm, Ef = 10 cm, BD = 4cm and DE = y cm 
In ΔECD and ΔEAB 

18. ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid- points of AB, AC, CD and BD respectively, show that PQRS is a rhombus. 

Solution

AD = BC and P, Q, R and S are the mid - points of sides AB, AC, CD and BD respectively, 
show that PQRS is a rhombus.
In ΔBAD, by mid - point theorem 
PS || AD and PS = 1/2AD ...(i) 
In ΔCAD, by mid - point theorem 
QR || AD and QR = 1/2 AD ...(ii) 
Compare (i) and (ii) 
PS ||QR and PS = QR 
Since one pair of opposite sides is equal as well as parallel then PQRS is a parallelogram     ....(iii) 
Now, In ΔABC, by mid - point theorem 
PQ || BC and PQ= 1/2 BC ...(iv) 

19. In Fig. below, if AB ⊥ BC, DC⊥BC and DE⊥AC, Prove that  ΔCED ～ΔABC. 

Solution

20. In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC². Prove that ΔAPC ～ΔBCQ. 

Solution

21. A girl of height 90 cm is walking away from the base of a lamp - post at a speed of 1.2 m/sec. If the lamp is 3.6m above the ground, find the length of her shadow after 4 seconds. 

Solution

 

∴ Length of shadow  = 1.6m 

22. Diagonals AC and BD of a trapezium ABCD with AB|| DC intersect each other at the point O. Using similarity criterion for two triangles, show that  OA/OC = OB/OD . 

Solution

23. If ΔABC and ΔAMP are two right triangles, right angled at B and M respectively such that ∠BAC. Prove that 
(i) ΔABC ～ ΔAMP 
(ii) CA/PA = BC/MP 

Solution

24. A vertical stick of length 6m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28m long. Find the height of the tower. 

Solution

25. In below Fig., ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ～ΔADE and Hence find the lengths of AE and DE. 

Solution