RS Aggarwal Class 10 Solutions Chapter 9 Mean, Mode and Median Exercise 9E

RS Aggarwal Solutions Chapter 9 Mean, Mode and Median Exercise 9E Class 10 Maths

Chapter Name	RS Aggarwal Chapter 9 Mean, Mode and Median
Book Name	RS Aggarwal Mathematics for Class 10
Other Exercises	Exercise 9A Exercise 9B Exercise 9C Exercise 9D Exercise 9F
Related Study	NCERT Solutions for Class 10 Maths

Exercise 9E Solutions

1. Find the median of the following data by making a ‘less than ogive’.

Marks	0 - 10	10 - 20	20 - 30	40 - 50	50 - 60	60 - 70	70 - 80	80 - 90	90 -100
Number of students	5	3	4	3	3	4	7	9	8

Solution

The frequency distribution table of less than type is given as follows:

Marks (upper class limits)	Cumulative Frequency (cf)
Less than 10	5
Less than 20	5 + 3 = 8
Less than 30	8 + 4 = 12
Less than 40	12 + 3 = 15
Less than 50	15 + 3 = 18
Less than 60	18 + 4 = 22
Less than 70	22 + 7 = 29
Less than 80	29 + 9 = 38
Less than 90	38 + 7 = 45
Less than 100	45 + 8 = 53

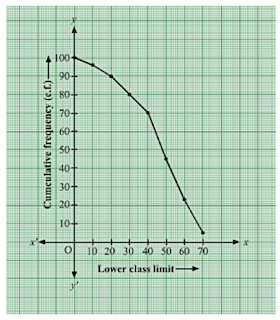
 Taking upper class limits of class intervals on x-axis and their respective frequencies on y-axis, its ogive can be drawn as follows:

Here, N = 53 ⇒ N/2 = 26.5

Mark the point A whose ordinate is 26.5 and its x-coordinate is 66.4.

Thus, median of the data is 66.4.

2. The given distribution shows the number of wickets taken by the bowlers in one-day international cricket matches:

Number of wickets	Less than 15	Less than 30	Less than 45	Less than 60	Less than 75	Less than 90	Less than 105	Less than 120
Number of bowlers	2	5	9	17	39	54	70	80

Draw a ‘less than type’ ogive from the above data. Find the median.

Solution

Taking upper class limits of class intervals on x-axis and their respective frequencies on y-axis, its ogive can be drawn as follows:

Here, N = 80 ⇒ N/2 = 40.

Mark the point a whose ordinate is 40 and its x-coordinate is 76.

Thus, median of the data is 76.

3. Draw a ‘more than’ ogive for the data given below which gives the marks of 100 students.

Marks	0 - 10	10 - 20	20 - 30	30 - 40	40 - 50	50 - 60	60 - 70	70 - 80
No. of students	4	6	10	10	25	22	18	5

Solution

The frequency distribution table of more than type is as follows:

Marks (upper class limits)	Cumulative frequency (cf)
More than 0	96 + 4 = 100
More than 10	90 + 6 = 96
More than 20	80 + 10 = 90
More than 30	70 + 10 = 80
More than 40	45 + 25 = 70
More than 50	23 + 22 = 45
More than 60	18 + 5 = 23
More than 70	5

Taking lower class limits of on x-axis and their respective cumulative frequencies on y-axis, its ogive can be drawn as follows:

4. The heights of 50 girls of Class X of a school are recorded as follows:

Height (in cm)	135 - 140	140 - 145	145 - 150	150 - 155	155 - 160	160 - 165
No. of students	5	8	9	12	14	2

Draw a ‘more than type’ ogive for the above data.

Solution

The frequency distribution table of more than type is as follows:

Height (in cm) (lower class limit)	Cumulative frequency (cf)
More than 135	5 + 45 = 50
More than 140	8 + 37 = 45
More than 145	9 + 28 = 37
More than 150	12 + 16 = 28
More than 155	14 + 2 = 16
More than 160	2

Taking lower class limits of an x-axis and their respective cumulative frequencies on y-axis, its ogive can be drawn as follows:

5. The monthly consumption of electricity (in units) of some families of a locality is given in the following frequency distribution:

Monthly Consumption (in units)	140 - 160	160 - 180	180 - 200	200 - 220	220 - 240	240 - 260	260 - 280
Number of Families	3	8	15	40	50	30	10

Prepare a ‘more than type’ ogive for the given frequency distribution.

Solution

The frequency distribution table of more than type is as follows:

Height (in cm) (lower class limit)	Cumulative frequency (cf)
More than 140	3 + 153 = 156
More than 160	8 + 145 = 153
More than 180	15 + 130 = 145
More than 200	40 + 90 = 130
More than 220	50 + 40 = 90
More than 240	30 + 10 = 40
More than 260	10

Taking the lower class limits of an x-axis and their respective cumulative frequencies on y-axis, its ogive can be drawn as follows:

 

6. The following table gives the production yield per hectare of wheat of 100 farms of a village.

Production Yield (kg/ha)	50 - 55	55 - 60	60 - 65	65 - 70	70 - 75	75 - 80
Number of farms	2	8	12	24	238	16

Change the distribution to a ‘more than type’ distribution and draw its ogive. Using ogive, find the median of the given data.

Solution

The frequency distribution table of more than type is as follows:

Production yield (kg/ha) (lower class limits)	Cumulative frequency (cf)
More than 50	2 + 98 = 100
More than 55	8 + 90 = 98
More than 60	12 + 78 = 90
More than 65	24 + 54 = 78
More than 70	38 + 16 = 54
More than 75	16

Taking the lower class limits on x-axis and their respective cumulative on y-axis, its ogive can be drawn as follows:

Here, N = 100

⇒ N/2 = 50.

Mark the point A whose ordinate is 50 and its x-coordinate is 70.5.

Thus, median of the data is 70.5.

7. The table given below shows the weekly expenditures on food of some households in a locality.

Weekly expenditure (in ₹)	No. of house holds
100 - 200	5
200 - 300	6
300 - 400	11
400 - 500	13
500 - 600	5
600 - 700	4
700 - 800	3
800 - 900	1

Draw a ‘less than type ogive’ and a ‘more than type ogive’ for this distribution.

Solution

The frequency distribution table of less than type is as follows:

Weekly expenditure (in ₹) (upper class limits)	Cumulative frequency (cf)
Less than 200	5
Less than 300	5 + 6 = 11
Less than 400	11 + 11 = 22
Less than 500	22 + 13 = 35
Less than 600	35 + 5 = 40
Less than 700	40 + 4 = 44
Less than 800	44 + 3 = 47
Less than 900	47 + 2 = 49

Taking the lower class limits on x-axis and their respective cumulative frequencies on y-axis, its ogive can be obtained as follows:

Now, the frequency distribution table of more than type is as follows:

Weekly expenditure (in ₹) (lower class limits)	Cumulative frequency (cf)
More than 100	44 + 5 = 49
More than 200	38 + 6 = 44
More than 300	27 + 11 = 38
More than 400	14 + 13 = 27
More than 500	9 + 5 = 14
More than 600	5 + 4 = 9
More than 700	2 + 3 = 5
More than 800	2

Taking the lower class limits on x-axis and their respective cumulative frequencies on y-axis, its ogive can be obtained as follows:

8. From the following frequency, prepare the ‘more than’ ogive.

Score	Number of candidates
400 - 450	20
450 - 500	35
500 - 550	40
550 - 600	32
600 - 650	24
650 – 700	27
700 – 750	18
750 – 800	34
Total	230

Also, find the median.

Solution

From the given table, we may prepare than ‘more than’ frequency table as shown below:

Score	Number of candidates
More than 750	34
More than 700	52
More than 650	79
More than 600	103
More than 550	135
More than 500	175
More than 450	210
More than 400	230

We plot the points A(750, 34), B(700, 52), C(650, 79), D(600, 103), E(550, 135), F(500, 175), G(450, 210) and H(400, 230).

Join AB, BC, CD, DE, EF, FG, GH and HA with a free hand to get the curve representing the ‘more than type’ series.

Here, N = 230

⇒ N/2 = 115

From P(0, 115), draw PQ meeting the curve at Q. Draw QM meeting at M.

Clearly, OM = 590 units

Hence, median = 590 units.

9. The marks obtained by 100 students of a class in an examination are given below:

Marks	Number of students
0 - 5	2
5 - 10	5
10 – 15	6
15 – 20	8
20 - 25	10
25 – 30	25
30 - 35	20
35 - 40	18
40 – 45	4
45 - 50	2

Draw cumulative frequency curves by using (i) ‘less than’ series and (ii) ‘more than’ series. Hence, find the median.

Solution

(i) From the given table, we may prepare the ‘less than’ frequency table as shown below:

Marks	Number of students
Less than 5	2
Less than 10	7
Less than 15	13
Less than 20	21
Less than 25	31
Less than 30	56
Less than 35	76
Less than 40	94
Less than 45	98
Less than 50	100

We plot the points A(5, 2), B(10, 7), C(15, 13), D(20, 21), E(25, 31), F(30, 56), G(35, 76) and H(40, 94), I(45, 98) and j(50, 100).

Join AB, BC, CD, DE, EF, FG, GH, HI, IJ and JA with a free hand to get the curve representing the ‘less than type’ series.

(ii) More than series:

Marks	Number of students
More than 0	100
More than 5	98
More than 10	93
More than 15	87
More than 20	79
More than 25	69
More than 30	44
More than 35	24
More than 40	6
More than 45	2

Now, on the same graph paper, we plot the points (0, 100), (5, 98), (10, 94), (15, 76),, (20, 56), (25, 31), (30, 21), (35, 13), (40, 6) and (45, 2).

Join with a free hand to get the ‘more than type’ series.

The two curves intersect at point. Draw LM ⊥ OX cutting the x-axis at M.

Clearly, M = 29.5

Hence, Median = 29.5

10. From the following data, draw the two types of cumulative frequency curves and determine the median:

Marks	Frequency
140 - 144	3
144 - 148	9
148 - 152	24
152 - 156	31
156 - 160	42
160 - 164	64
164 – 168	75
168 – 172	82
172 – 176	86
176 - 180	34

Solution

(i) Less than series:

Marks	No. of students
Less than 144	3
Less than 148	12
Less than 152	36
Less than 156	67
Less than 160	109
Less than 164	173
Less than 168	248
Less than 172	230
Less than 176	416
Less than 180	450

We plot the points A(144, 3), B(148, 12), C(152, 36), D(156, 67), E(160, 109), F(164, 173), G(168, 248) and H(172, 330), I(176, 416) and J(180, 450).

Join AB, BC, CD, DE, EF, FG, GH, HI, IJ and JA with a free hand to get the curve representing the ‘less than type’ series.

(ii) More than series:

Marks	Number of students
More than 140	450
More than 144	447
More Than 148	438
More than 152	414
More than 156	383
More than 160	341
More than 164	277
More than 168	202
More than 172	120
More than 176	34

Now, on the same graph paper, we plot the points A₁ (140, 150), B₁(144, 447), C₁(148, 438), D₁(152, 414), E₁(156, 383), F₁(160, 277), H₁(168, 202), I₁(172, 120) and J₁ (176, 34),

Join A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁F₁, F₁G₁, G₁H₁, H₁I₁ and I₁J₁ with a free hand to get the ‘more than type’ series.

The two curves intersect at point L. Draw LM ⊥ OX cutting the x-axis at M. Clearly M = 166 cm

Hence, median = 166 cm