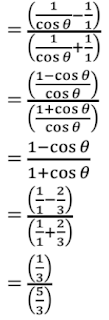RS Aggarwal Solutions Chapter 8 Trigonometric Identities Exercise 8C Class 10 Maths
Chapter Name | RS Aggarwal Chapter 8 Trigonometric Identities |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 8C Solutions
1. Write the value of (1 – sin2 θ) sec2 θ.
Solution
(1 – sin2 θ) sec2 θ
= cos2 θ × 1/cos θ
= 1
2. Write the value of (1 – cos2 θ) cosec2 θ.
Solution
(1 – cos2 θ) cosec2 θ
= sin2 θ × 1/sin2 θ
= 1
3. Write the value of (1 + tan2 θ) cos2θ.
Solution
(1 + tan2 θ) cos2 θ
= sec2θ × 1/sec2 θ
= 1
4. Write the value of (1 + cot2 θ) sin2 θ.
Solution
(1 + cot2 θ) sin2 θ
= cosec2 θ × 1/cosec2 θ
= 1
5. Write the value of (sin2 θ + 1+ tan2 θ).
Solution
(sin2 θ + (1 + tan2 θ)
= (sin2 θ + 1/sec2 θ)
= (sin2 θ + cos2 θ)
= 1
6. Write the value of (cot2 θ – 1/sin2 θ).
Solution
(cot2 θ – 1/sin2 θ)
= (cot2 θ – cosec2 θ)
= - 1
7. Write the value of sin θ cos(90° - θ) + cos θ sin (90° - θ).
Solution
sin θ cos(90° - θ) + cos θ sin(90° - θ)
= sin θ sin θ + cos θ cos θ
= sin2 θ + cos2 θ
= 1
8. Write the value of cosec2 (90° - θ) – tan2 - θ.
Solution
cosec2 (90° - θ) – tan2 θ
= sec2 θ – tan2 θ
= 1
9. Write the value of sec2 θ(1 + sin – θ)(1 – sin – θ).
Solution
sec2 θ(1 + sin θ)(1 – sin θ)
= sec2 θ(1 – sin2 θ)
= 1/cos2 θ × cos2 θ
= 1
10. Write the value of cosec2 θ(1 + cos θ)(1 – cos θ).
Solution
cosec2 θ(1 + cos θ)(1 – cos θ)
= cosec2 θ(1 – cos2 θ)
= 1/sin2 θ × sin2 θ
= 1
11. Write the value of sin2 θ cos2 θ(1 + tan2 θ)(1 + cot2 θ).
Solution
sin2 θ cos2 θ(1 + tan2 θ)(1+ cot2 θ)
= sin2 θ cos2 θ sec2 θ cosec2 θ
= sin2 θ × cos2 θ × 1/cos2 θ × 1/sin2 θ
= 1
12. Write the value of (1 + tan2 θ)(1 + sin θ)(1 – sin θ)
Solution
(1 + tan2 θ)(1 + sin θ)(1 – sin θ)
= sec2 θ(1 – sin2 θ)
= 1/cos2 θ × cos2 θ
= 1
13. Write the value of (1 + tan2 θ)(1 + sin θ)(1 – sin θ).
Solution
3 cot2 θ – 3cosec2 θ
= 3(cot2 θ – cosec2 θ)
= 3(-1)
= - 3
14. Write the value of 3 cot2 θ – 3 cosec2 θ.
Solution
4 tan2 θ – 4/cos2 θ
= 4 tan2 θ – 4 sec2 θ
= 4(tan2 θ – sec2 θ)
= 4(-1)
= -4
15. Write the value of (tan2 θ – sec2 θ)/(cot2 θ – cosec2 θ).
Solution
(tan2 θ – sec2 θ)/(cot2 θ – cosec2 θ)
= -1/-1
= 1
16. If sin θ = 1/2, write the value of (3 cot2θ + 3).
Solution
As sin θ = 1/2
So, cosec θ = 1/sin θ = 2 ...(i)
Now.
3 cot2 θ + 3
= 3(cot2 θ + 1)
= 3 cosec2 θ
= 3(2)2 [Using (i)]
= 3(4)
= 12
17. If cos θ = 2/3, write the value of (4 + 4 tan2 θ).
Solution
4 + 4 tan2 θ
= 4(1 + tan2 θ)
= 4 sec2 θ
= 4/cos2 θ
= 4/(2/3)2
= 4/(4/9)
= (4 × 9)/4
= 9
18. If cos θ = 7/25, write the value of (tan θ + cot θ).
Solution
As sin2 θ = 1 – cos2 θ
= 1 – (7/25)2
= 1 – 49/625
= (625 – 49)/625
⇒ sin2 θ = 576/625
⇒ sin θ = 24/25
Now, tan θ + cot θ
= sin θ/cos θ + cos θ/sin θ
= (sin2 θ + cos2 θ)/(cos θ sin θ)
= 1/(7/25 × 24/25)
= 1/(168/625)
= 625/168
19. If cos θ = 2/3, write the value of (sec θ – 1)/(sec θ + 1).
Solution
(sec θ – 1)/(sec θ + 1)
= 1/5
20. If 5 tan θ = 4, write the value of (cos θ – sin θ)/(cos θ + sin θ).
Solution
We have,
5 tan θ = 4
⇒ tan θ = 4/5
Now,
(cos θ – sin θ)/(cos θ + sin θ)
Solution
We have:
3 cot θ = 4
⇒ cot θ = 4/5
Now,
(2 cos θ – sin θ)/(cos θ + sin θ)
22. If cot θ = 1/√3, write the value of (1 – cos2 θ)/(2 – sin2 θ).
Solution
We have:
Cot θ = 1/√3
⇒ cot θ = cot (Ï€ /3)
⇒ θ = Ï€/3
Now,
Solution
(cosec2 θ – sec2 θ)/(cosec2 θ – sec2 θ)
Solution
We have:
cot A = 4/3
⇒ cot (90° - B) = 4/3 (As A + B = 90°)
∴ tan B = 4/3
25. If cos B = 3/5 and (A + B) = 90°, find the value of sin A.
Solution
We have,
cos B = 3/5
⇒ cos(90° - A) = 3/5 (As, A + B = 90°)
∴ sin A = 3/5
26. If √3 sin θ = cos θ and θ is an acute angle, find the value of θ.
Solution
We have,
√3 sin θ = cos θ
⇒ sin θ/cos θ = 1/√3
⇒ tan θ = 1/√3
⇒ tan θ = tan 30°
∴ θ = 30°
27. Write the value of tan 10° tan 20° tan 70° tan 80°.
Solution
tan 10° tan 20° tan 70° tan 80°
= cot (90° - 10°) cot (90° - 20°) tan 70° tan 80°
= cot 80° cot 70° tan 70° tan 80°
= 1/tan 80° × 1/tan 70° × tan 70° × tan 80°
= 1
28. Write the value of tan 1° tan 2° ...... tan 89°.
Solution
tan 1° tan 2° ...... tan 89°
= tan 1° tan 2° tan 3° ........ tan 45° ........ tan 87° tan 88° tan 89°
= tan 1° tan 2° tan 3° .......tan 45° .......cot(90° - 87°) cot(90° - 88°) cot(90° - 89°)
= tan 1° tan 2° tan 3° ..... tan 45° ....cot 3° cot 2° cot 1°
= tan 1° × tan 2° × tan 3° × ...... × 1 × ..... × 1/tan 3° × 1/tan 2° × 1/tan 1°
= 1
29. Write the value of cos 1° cos 2° .........cos 180°.
Solution
cos 1° cos 2° .......cos 180°
= cos 1° cos 2° .......cos 90° ......cos 180°
= cos 1° cos 2° ......0 ......cos 180°
= 0
30. If tan A = 5/12, find the value of (sin A + cos A) sec A.
Solution
(sin A + cos A sec A)
= (sin A + cos A) 1/cos A
= sin A/cos A + cos A/cos A
= tan A + 1
= 5/12 + 1/1
⇒ (5 + 12)/12
= 17/12
31. If sin θ cos (θ - 45°), where θ is acute, find the value of θ.
Solution
We have,
sin θ = cos (θ – 45°) θ
⇒ cos (90° - θ) = cos (θ - 45°)
Comparing both sides, we get
90° - θ = θ - 45°
⇒ θ + θ = 90° + 45°
⇒ 2θ = 135°
⇒ θ = (135/2)°
∴ θ = 67.5°
32. Find the value of sin 50°/cos 40° + cosec 40°/sec 50° - 4 cos 50° cosec 40°.
Solution
sin 50°/cos 40° + cosec 40°/sec 50° - 4 cos 50° cosec 40°
= cos(90° - 50°)/cos 40° + sec(90° - 40°)/sec 50° - 4 sin (90° - 50°) cosec 40°
= cos 40°/cos 40° + sec 50°/sec 50° - 4 sin 40° × 1/ sin 40°
= 1 + 1 – 4
= - 2
33. Find the value of sin 48° sec 42° + cos 48° cosec 42°.
Solution
sin 48° sec 42° + cos 48° cosec 42°
= sin 48° cosec (90° - 42) + cos 48° sec (90° - 42°)
= sin 48° cosec 48° + cos 48° sec 48°.
= sin 48° × 1/ sin 48° + cos 48° × 1/cos 48°
= 1 + 1
= 2
34. If x = a sin θ and y = b cos θ, write the value of (b2x2 + a2y2).
Solution
(b2x2 + a2x2)
= b2 (a sin θ)2 + a2(b cos θ)2
= b2a2 sin2 θ + a2b2 cos2 θ
= a2b2 (sin2 θ + cos2 θ)
= a2b2(1)
= a2b2
35. If 5x = sec θ and 5/x = tan θ, find the value of 5(x2 – 1/x2).
Solution
5(x2 – 1/x2)
= 25/5(x2 – 1/x2)
= 1/5(25x2 – 25/x2)
= 1/5[(5x)2 – (5/x)2]
= 1/5[(sec θ)2 – (tan θ)2]
= 1/5(sec2 θ – tan2 θ)
= 1/5 (1)
= 1/5
36. If cosec θ = 2x and cot θ = 2/x, find the value of 2(x2 – 1/x2)
Solution
2(x2 – 1/x2)
= 4/2(x2 – 1/x2)
= 1/2(4x2 – 4/x2)
= 1/2[(2x2 – (2/x)2]
= 1/2[(cosec θ)2 – sec θ)2]
= 1/2(cosec2 θ – sec2 θ)
= 1/2(1)
= 1/2
37. If sec θ + tan θ = x, find the value of sec θ.
Solution
We have:
sec θ + tan θ = x ...(i)
⇒ (sec θ + tan θ)/1 × (sec θ - tan θ)/(sec θ - tan θ) = x
⇒ (sec2 θ - tan2 θ)/(sec θ - tan θ) = x
⇒ 1/(sec θ – tan θ) = x/1
⇒ sec θ – tan θ = 1/x ...(ii)
Adding (i) and (ii), we get
2 sec θ = x + 1/x
⇒ 2 sec θ = (x2 + 1)/x
∴ sec θ = (x2 + 1)/2x
38. Find the value of (cos 38° cosec 52°)/(tan 18° tan 35° tan 60° tan 72° tan 55°)
Solution
(cos 38° cosec 52°)/(tan 18° tan 35° tan 60° tan 72° tan 55°)
