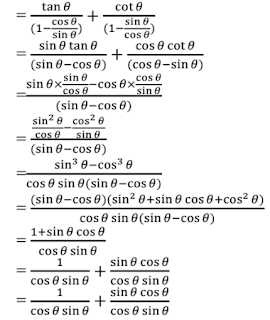RS Aggarwal Chapter 8 Trigonometric Identities Exercise 8A Class 10 Maths
Chapter Name | RS Aggarwal Chapter 8 Trigonometric Identities |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 8A Solutions
1. (i) (1 – cos2 θ) cosec2θ = 1
(ii) (1 + cot2θ) sin2 θ = 1
Solution
(i) LHS = (1 − cos2 θ) cosec2 θ
= sin2 θ cosec2 θ (∵ cos2 θ + sin2 θ = 1)
= 1/cosec2 θ × cosec2 θ
= 1
Hence, LHS = RHS
(ii) LHS = (1 + cot2 θ) sin2 θ
= cosec2 θ sin2 θ (∵ cosec2 θ − cot2 θ = 1)
= 1/sin2 θ × sin2 θ
= 1
Hence, LHS = RHS
2. (i) (sec2 θ – 1) cot2 θ = 1
(ii) (sec2 θ – 1)(cosec2 θ - 1) = 1
(iii) (1 – cos2 θ) sec2 θ = tan2 θ
Solution
(i) LHS = (sec2 θ − 1) cot2 θ
= tan2 θ × cot2 θ (∵ sec2 θ − tan2 θ = 1)
= 1/cot2 θ × cot2 θ
= 1
= RHS
(ii) LHS = (sec2 θ − 1)(cosec2 θ − 1)
= tan2 θ × cot2 θ (∵ sec2 θ − tan2 θ = 1)
= 1/cot2 θ × cot2 θ
= 1
= RHS
(iii) LHS = (1 - cos2 θ)sec2 θ
= sin2 θ × sec2 θ (∵ sin2 θ + cos2 θ = 1)
= sin2 θ × 1/cos2 θ
= sin2 θ/cos2 θ
= tan2 θ
= RHS
3. (i) sin2 θ + 1/(1 + tan2 θ) = 1
(ii) 1/(1 + tan2 θ) + 1/(1 + cot2 θ) = 1
Solution
(i) LHS = sin2 θ + 1/(1 + tan2 θ)
= sin2 θ + 1/sec2 θ (∵ sec2 θ − tan2 θ = 1)
= sin2 θ + cos2 θ
= 1
= RHS
(ii) LHS = 1/(1 + tan2 θ) + 1/(1 + cot2 θ)
= 1/sec2 θ + 1/cosec2 θ
= cos2 θ + sin2 θ
= 1
= RHS
4. (i) (1 + cos θ)(1 – cos θ)(1 + cos2 θ) = 1
(ii) cosec θ (1 + cos θ)(cosec θ – cot θ) = 1
Solution
(i) LHS = (1+ cos θ)/(1 – cos θ) (1 + cos2 θ)
= (1 – cos2 θ)(cosec2 θ)
= sin2 θ × cosec2 θ
= sin2 θ × 1/sin2 θ
= 1
= RHS
(ii) LHS = cosec θ(1 + cos θ)(cosec θ – cot θ)
= (cosec θ + cosec θ × cos θ)(cosec θ – cot θ)
= (cosec θ + 1/sin θ × cos θ)(cosec θ – cot θ)
= (cosec θ + cot θ)(cosec θ – cot θ)
= cosec2 θ – cot2 θ (∵ cosec2 θ - cot2 θ = 1)
= 1
= RHS
5. (i) cot2 θ - 1/sin2 θ = -1
(ii) tan2 θ – 1/cos2 θ = - 1
(iii) cos2 θ + 1/(1 + cot2 θ) = 1
Solution
(i) cot2 θ - 1/sin2 θ = -1
= cos2 θ/sin2 θ – 1/sin2 θ
= (cos2 θ - 1)/sin2 θ
= - sin2 θ /sin2 θ
= - 1
= RHS
(ii) LHS = tan2 θ – 1/cos2 θ
= sin2 θ/cos2 θ – 1/cos2 θ
= (sin2 θ – 1)/cos2 θ
= -cos2 θ/cos2 θ
= - 1
= RHS
(iii) LHS = cos2 θ + 1/(1 + cot2 θ)
= cos2 θ + 1/cosec2 θ
= cos2 θ + sin2 θ
= 1
= RHS
6. 1/(1 + sin θ) + 1/(1 – sin θ) = 2 sec2 θ
Solution
LHS = 1/(1 + sin θ) + 1/(1 – sin θ)
= (1 – sin θ) + (1 + sin θ) /(1 + sin θ)(1 – sin θ)
= 2/(1 – sin2 θ)
= 2/cos2 θ
= 2 sec2 θ
= RHS
7. (i) sec θ(1 – sin θ)(sec θ + tan θ) = 1
(ii) sin θ (1 + tan θ) + cos θ(1 + cot θ) = sec θ + cosec θ)
Solution
(i) LHS = sec θ(1 – sin θ)(sec θ + tan θ)
= (sec θ – sec θ sin θ)(sec θ + tan θ)
= (sec θ – 1/cos θ × sin θ) (sec θ + tan θ)
= (sec θ – tan θ)(sec θ + tan θ)
= sec2 θ – tan2 θ
= 1
= RHS
(ii) LHS = sin θ(1 + tan θ) + cos θ(1 + cot θ)
= sin θ + sin θ × sin θ/cos θ + cos θ × cos θ/sin θ
= (cos θ sin2 θ + sin3 θ + cos2 θ sin θ + cos3 θ)/(cos θ sin θ)
= (sin3 θ + cos3 θ) + (cos θ sin2 θ + cos2 θ sin θ)/(cos θ sin θ)
= [(sin θ + cos θ)(sin2 θ – sin θ cos θ + cos2 θ) + sin θ cos θ (sin θ + cos θ)]/cos θ sin θ
= (sin θ + cos θ)(sin2 θ + cos2 θ – sin θ cos θ + sin θ cos θ)/(cos θ sin θ)
= (sin θ + cos θ)(1)/(cos θ sin θ)
= (sin θ)/(cos θ sin θ) + (cos θ)/(cos θ sin θ)
= 1/cos θ + 1/sin θ
= sec θ + cosec θ
= RHS
8. (i) 1 + cot2 θ/(1 + cosec θ) = cosec θ
(ii) 1 + tan2 θ/(1 + sec θ) = sec θ
Solution
(i) LHS = 1 + cot2 θ/(1 + cosec θ)
= 1 + (cosec2 θ – 1)/(cosec θ + 1) (∵ cosec2 θ – cot2 θ = 1)
= 1 + (cosec θ + 1)(cosec θ – 1)/(cosec θ + 1)
= 1 + (cosec θ – 1)
= cosec θ
= RHS
(ii) LHS = 1 + tan2 θ/(1 + sec θ)
= 1 + (sec2 θ – 1)/(sec θ + 1)
= 1 + {(sec θ + 1)(sec θ – 1)}/(sec θ + 1)
= 1 + (sec θ – 1)
= sec θ
= RHS
9. 1 + (tan2 θ) cot θ/(cosec2 θ) = tan θ
Solution
LHS = (1 + tan2 θ)cot θ/cosec2 θ
= (sec2 θ cot θ)/(cosec2 θ)
= (1/cos2 θ × cos θ/sin θ)/(1/sin2 θ)
= 1/(cos θ sin θ) × sin2 θ
= sin θ/cos θ
= tan θ
= RHS
Hence, LHS = RHS
10. tan2 θ/(1 + tan2 θ) + cot2 θ/(1 + cot2 θ) = 1
Solution
LHS = tan2 θ/(1 + tan2 θ) + cot2 θ/(1 + cot2 θ)
= tan2 θ/sec2 θ + cot2 θ/cosec2 θ (∵ sec2 θ – tan2 θ = 1 and cosec2 θ – cot2 θ = 1)
= (sin2 θ/cos2 θ)/(1/cos2 θ) + (cos2 θ/sin2 θ)/(1/sin2 θ)
= sin2 θ + cos2 θ
= 1
= RHS
Hence, LHS = RHS
11. sin θ/(1 + cos θ) + (1 + cos θ)/sin θ = 2 cosec θ
Solution
LHS = sin (1 + cos θ) + (1 + cos θ)/sin θ
= sin2 θ + (1 + cos θ)2/(1 + cos θ) sin θ
= sin2 θ + 1 + cos2 θ + 2 cos θ)/)(1 + cos θ) sin θ
= (1 + 1 + 2 cos θ)/(1 + cos θ) sin θ
= (2 + 2 cos θ)/(1 + cos θ) sin θ
= 2(1 + cos θ)/(1 + cos θ) sin θ
= 2/sin θ
= 2 cosec θ
= RHS
Hence, L.H.S = R.H.S
12. tan θ/(1 – cot θ) + cot θ/(1 – tan θ) = (1 + sec θ cosec θ)
Solution
tan θ/(1 – cot θ) + cot θ/(1 – tan θ)
= 1 + sec θ cosec θ
= RHS
13. cos2 θ/(1 – tan θ) + sin3 θ/(sin θ – cos θ) = (1 + sin θ cos θ)
Solution
cos2 θ/(1 – tan θ) + sin3 θ/(sin θ – cos θ) = (1 + sin θ cos θ)
LHS = cos2 θ/(1 – tan θ) + sin3 θ/(sin θ – cos θ)
= (sin2 θ + cos2 θ + cos θ sin θ)
= (1 + sin θ cos θ)
= RHS
Hence, L.H.S. = R.H.S.
14. cos θ/(1 – tan θ) + sin2 θ/(cos θ – sin θ)
Solution
LHS = cos θ/(1 – tan θ) – sin2 θ/(cos θ – sin θ)
= (cos θ + sin θ)
= RHS
Hence, LHS = RHS
15. (1 + tan2 θ)(1 + cot2 θ) = 1/(sin2 θ – sin4 θ)
Solution
L.H.S. = (1 + tan2 θ)(1 + cot2 θ)
= sec2 θ. cosec2 θ (∵ sec2 θ – tan2 θ = 1 and cosec2 θ – cot2 θ = 1)
= 1/cos2 θ. sin2 θ
= 1/(1 – sin2 θ)sin2 θ
= 1/sin2 θ – sin4 θ
= RHS
Hence, LHS = RHS
16. tan θ/(1 + tan2 θ)2 + cot θ/(1 + cot2 θ)2 = sin θ cos θ
Solution
L.H.S. = tan θ/(1 + tan2 θ) + cot θ/(1 + cot2 θ)2
= tan θ/(sec2 θ)2 + cot θ/(cosec2 θ)2
= tan θ/sec4 θ + cot θ/cosec4 θ
= sin θ/cos θ × cos4 θ + cos θ/sin θ × sin4 θ
= sin θ cos3 θ + cos θ sin3 θ
= sin θ cos θ (cos2 θ + sin2 θ)
= sin θ cos θ
= RHS
17. (i) sin6 θ + cos6 θ = 1 – 3 sin2 θ cos2 θ
(ii) sin2 θ + cos4 θ = cos2 θ + sin4 θ
(iii) cosec4 θ + cosec2 θ = cot4 θ + cot2 θ
Solution
(i) LHS = sin6 θ + cos6 θ
= (sin2 θ)3 + cos2 θ)3
= (sin2θ + cos2 θ)(sin4 θ – sin2 θ cos2 θ + cos4 θ)
= 1 × {(sin2 θ)2 + 2 sin2 θ cos2 θ + (cos2 θ)2 – 3 sin2 θ cos2 θ}
= (sin2 θ + cos2 θ)2 – 3 sin2 θ cos2 θ
= (1)2 – 3 sin2 θ cos2 θ
= 1 – 3 sin2 θ cos2 θ
= RHS
Hence, LHS = RHS
(ii) LHS = sin2 θ + cos4 θ
= sin2 θ + (cos2 θ)2
= sin2 θ + (1 – sin2 θ)2
= sin2 θ + 1 – 2 sin2 θ + sin4 θ
= 1 – sin2 θ + sin4 θ
= cos2 θ + sin4 θ
= RHS
Hence, LHS = RHS
(iii) LHS = cosec4 θ – cosec2 θ
= cosec2 θ(cosec2 θ – 1)
= cosec2 θ × cot2 θ (∵ cosec2 θ – cot2 θ = 1)
= (1 + cot2 θ) × cot2 θ
= cot2 θ + cot4 θ
= RHS
Hence, LHS = RHS
18. (i) (1 – tan2 θ)/(1 + tan2 θ) = (cos2 θ – sin2 θ)
(ii) (1 – tan2 θ)/(cot2 – 1) = tan2 θ
Solution
(i) LHS = (1 – tan2 θ)/(1 + tan2 θ)
= (cos2 θ – sin2 θ)/(cos2 θ + sin2 θ)
= (cos2 θ – sin2 θ)/1
= cos2 θ – sin2 θ
= RHS
(ii) LHS = (1 – tan2 θ)/(cot2 θ – 1)
= tan2 θ
= RHS
19. (i) tan θ/(sec θ – 1) + tan θ/(sec θ + 1) = 2 cosec θ
(ii) cot θ/(cosec θ + 1) + cosec θ + 1)/cot θ) = 2 sec θ
Solution
(i) LHS = tan θ/(sec θ – 1) + tan θ/(sec θ + 1)
(ii) LHS = cot θ/(cosec θ + 1) + (cosec θ + 1)/cot θ
= 2 × 1/sin θ × sin θ/cos θ
= 2 sec θ
= RHS
Hence, LHS = RHS
20. (i) (sec θ – 1)/(sec θ + 1) = sin2 θ/(1 + cos θ)2
(ii) (sec θ – tan θ)/(sec θ + tan θ) = cos2 θ/(1 + sin θ)2
Solution
(i) LHS = (sec θ – 1)/(sec θ + 1)
= (1 - sin2 θ)/(1 + sin θ)2
= cos2 θ/(1 + sin θ)2
= RHS
21. (i) √(1+sinθ)/(1-sinθ) = (secθ + tanθ)
(ii) √(1-cosθ)/(1+cosθ) = (cosecθ - cotθ)
(iii) √(1+cosθ)/(1-cosθ) = 2cosecθ
Solution
(i) LHS
= (1 + sin θ)/cos θ
= 1/cos θ + sin θ/cos θ
= (sec θ + tan θ)
= RHS
(ii) LHS
= (1 + cos θ +
1 - cos θ)/sin θ
= 2/sin θ
= 2 cosec θ
= RHS
22. (cos3 θ + sin3 θ)/(cos θ + sin θ) + (cos3 θ - sin3 θ)/(cos θ – sin θ) = 2
Solution
LHS = (cos3 θ + sin3 θ)/(cos θ + sin θ) + (cos3 θ – sin3 θ)/(cos θ – sin θ)
= (cos2 θ + sin2 θ – cos θ sin θ) + (cos2 θ + sin2 θ + cos θ sin θ)
= (1 – cos θ sin θ) + (1 + cos θ sin θ)
= 2
= RHS
Hence, LHS = RHS
23. sin θ/(cot θ + cosec θ) – sin θ/(cot θ – cosec θ) = 2
Solution
LHS = sin θ/(cot θ + cosec θ) – sin θ/(cot θ – cosec θ)
= sin θ × 2 × 1/sin θ
= 2
= RHS
24. (i) (sin θ – cos θ)/(sin θ + cos θ) + (sin θ + cos θ)/(sin θ – cos θ) = 2/(2 sin2 θ – 1)
(ii) (sin θ + cos θ)/(sin θ – cos θ) + (sin θ – cos θ)/(sin θ + cos θ) = 2/(1 – 2 cos2 θ)
Solution
(i) LHS = (sin θ – cos θ)/(sin θ + cos θ) + (sin θ + cos θ)/(sin θ – cos θ)
(ii) LHS = (sin θ + cos θ)/(sin θ - cos θ) + (sin θ - cos θ)/(sin θ + cos θ)
Solution
LHS = (1 + cos θ – sin2 θ)/{sin θ(1 + cos θ)}
= (1 + cos θ) – (1 – cos2 θ)/sin θ(1 + cos θ)
= (cos θ + cos2 θ)/sin θ(1 + cos θ)
= cos θ(1 + cos θ)/sin θ(1 + cos θ)
= cos θ/sin θ
= cot θ
= RHS
Hence, L.H.S = R.H.S.
26. (i) (cosec θ + cot θ)/(cosec θ – cot θ) = (cosec θ + cot θ)2 = 1 + 2 cot2 θ + 2 cosec θ cot θ
(ii) (sec θ + tan θ)/(sec θ – tan θ)2 = (sec θ + tan θ)2 = 1 + 2 tan2 θ + 2 sec θ tan θ
Solution
(i) Here, (cosec θ + cot θ)/(cosec θ – cot θ)
= (cosec θ + cot θ)(cosec θ + cot θ)/(cosec θ – cot θ)(cosec θ + cot θ)
= (cosec θ + cot θ)2/(cosec2 θ – cot2)
= (cosec θ + cot θ)2/1
= (cosec θ + cot θ)2/1
= (cosec θ + cot θ)2
Again, (cosec θ + cot θ)2
= cosec2 θ + cot2 θ + 2cosec θ cot θ
= 1 + cot2 θ + cot2 θ + 2 cosec θ cot θ (∵ cosec2 θ – cot2 θ = 1)
= 1 + 2 cot2 θ + 2 cosec θ cot θ
(ii) Here, (sec θ + tan θ)/(sec θ – tan θ)
= (sec θ + tan θ)(sec θ + tan θ)/(sec θ + tan θ)(sec θ + tan θ)
= (sec θ + tan θ)2/(sec θ – tan2 θ)
= (sec θ + tan θ)2/1
= (sec θ + tan θ)2
Again, (sec θ + tan θ)2
= sec2 θ + tan2 θ + 2 sec θ tan θ
= 1 + tan2 θ + tan2 θ + 2sec θ tan θ
= 1 + 2 tan2 θ + 2 sec θ tan θ
27. (i) (1 + cos θ + sin θ)/(1 + cos θ – sin θ) = (1 + sin θ)/cos θ
(ii) (sin θ + 1 – cos θ)/(cos θ – 1 + sin θ) = (1 + sin θ)/cos θ
Solution
(i) LHS = (1 + cos θ + sin θ)/(1 + cos θ – sin θ)
= (2 sin2 θ + 2 sin θ)/(2 sin θ cos θ)
= 2 sin θ(1 + sin θ)/2 sin θ cos θ
= (1 + sin θ)/cos θ
= RHS
28. sin θ/(sec θ + tan θ – 1) + cos θ/(cosec θ + cot θ – 1) = 1
Solution
LHS = sin θ/(sec θ + tan θ + 1) + cos θ/(cosec θ + cot θ – 1)
= (sin θ cos θ)/(1 + sin θ – cos θ) + cos θ sin θ/(1 + cos θ – sin θ)
Solution
We have (sin θ + cos θ)/(sin θ – cos θ) + (sin θ – cos θ)/(sin θ + cos θ)
= (sin θ + cos θ)2 + (sin θ – cos θ)2/(sin θ – cos θ)(sin θ + cos θ)
= (sin2 θ + cos2 θ + 2 sin θ cos θ + sin2 θ + cos2 θ – 2 sin θ cos θ)/(sin2 θ – cos2 θ)
= (1 + 1)/(sin2 θ – cos2 θ)
= 2/(sin2 θ – cos2 θ)
Again, 2/(sin2 θ – cos2 θ)
= 2/(sin2 θ – (1 – sin2 θ))
= 2/(2 sin2 θ – 1)
30. (cos θ cosec θ – sin θ sec θ)/(cos θ + sin θ) = cosec θ – sec θ
Solution
LHS = (cos θ cosec θ – sin θ sec θ)/(cos θ + sin θ)
= 1/sin θ – 1/cos θ
= cosec θ – sec θ
= RHS
Hence, LHS = RHS
31. (1 + tan θ + cot θ)(sin θ – cos θ) = (sec θ/cosec2 θ - cosec θ/sec2 θ)
Solution
LHS = (1 + tan θ + cot θ)(sin θ – cos θ)
= sin θ + tan θ sin θ + cot θ sin θ – cos θ – tan θ cos θ – cot θ cos θ
= sin θ + tan θ sin θ + cos θ/sin θ × sin θ – cos θ – sin θ/cos θ × cos θ – cot θ cos θ
= sin θ + tan θ sin θ + cos θ – cos θ – sin θ – cot θ cos θ
= tan θ sin θ – cot θ cos θ
= sin θ/cos θ × 1/cosec θ × sec θ – 1/sec θ × 1/sec θ × cosec θ
= sec θ/cosec2 θ – cosec θ/sec2 θ
= RHS
Hence, LHS = RHS
32. cot2 θ(sec θ – 1)/(1 + sin θ) + sec2 θ(sin θ – 1)/(1 + sec θ) = 0
Solution
LHS = cot2 θ(sec θ – 1)/(1 + sin θ) + sec2 θ(sin θ – 1)/(1 + sec θ)
Solution
LHS = {1/sec2 θ – cos2 θ + 1/cosec2 θ – sin2 θ)}(sin2 θ cos2 θ)
Solution
LHS = (sin A – sin B)/(cos A + cos B) + (cos A – cos B)/(sin A + sin B)
= (sin A – sin B)(sin A + sin B) + (cos A – cos B)(cos A – cos B) /(cos A + cos B)(sin A + sin B)
= sin2 A – sin2 B + cos2 A – cos2 B)/(cos A + cos B)(sin A + sin B)
= 0/(cos A + cos B)(sin A + sin B)
= 0
= RHS
35. (tan A + tan B)/(cot A + cot B) = tan A tan B
Solution
LHS = (tan A + tan B)/(cot A + cot B)
= tan A tan B
= RHS
Hence, LHS = RHS
36. Show that none of the following is an identity:
(i) cos2 θ + cos θ = 1
(ii) sin2 θ + sin θ = 2
(iii) tan2 θ + sin θ = cos2 θ
Solution
(i) cos2 θ + cos θ = 1
LHS = cos2 θ + cos θ
= 1 – sin2 θ + cos θ
= 1 – (sin2 θ - cos θ)
Since, LHS ≠ RHS, this not an identity.
(ii) sin2 θ + sin θ = 1
LHS = sin2 θ + sin θ
= 1 – cos2 θ + sin θ
= 1 – (cos2 θ - sin θ)
Since LHS ≠ RHS, this not an identity.
(iii) tan2 θ + sin θ = cos2 θ
LHS = tan2θ + sin θ
= sin2 θ /cos2 θ + sin θ
= (1 – cos2 θ)/cos2 θ + sin θ
= sec2 θ - 1 + sin θ
Since LHS ≠ RHS, this is not an identity.
37. Prove that (sin θ - 2 sin3 θ) = (2 cos3 θ - cos θ) tan θ
Solution
RHS = (2 cos3 θ – cos θ) tan θ
= (2 cos2 θ – 1) cos θ × sin θ/cos θ
= [2(1 – sin2 θ) – 1] sin θ
= (2 – 2 sin2 θ – 1) sin θ
= (1 – 2 sin2 θ) sin θ
= (sin θ – 2 sin3 θ)
= LHS