RS Aggarwal Solutions Chapter 4 Triangles Exercise 4E Class 10 Maths

Chapter Name | RS Aggarwal Chapter 4 Triangles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 4E Solutions
1. State the two properties which are necessary for given two triangles to be similar.
Solution
The two triangles are similar if and only if
- The corresponding sides are in proportion.
- The corresponding angles are equal.
2. State the basic proportionality theorem.
Solution
If a line is draw parallel to one side of a triangle intersect the other two sides, then it divides the other two sides in the same ratio.
3. State and converse of Thale’s theorem.
Solution
If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
4. State the midpoint theorem
Solution
The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is equal to one half of the third side.
5. State the AAA-similarity criterion
Solution
If the corresponding angles of two triangles are equal, then their corresponding sides are proportional and hence the triangles are similar.
6. State the AA-similarity criterion
Solution
If two angles are correspondingly equal to the two angles of another triangle, then the two triangles are similar.
7. State the SSS-similarity criterion for similarity of triangles
Solution
If the corresponding sides of two triangles are proportional then their corresponding angles are equal, and hence the two triangles are similar.
8. State the SAS-similarity criterion
Solution
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional then the two triangles are similar.
9. State Pythagoras theorem
Solution
The square of the hypotenuse is equal to the sum of the squares of the other two sides. Here, the hypotenuse is the longest side and it’s always opposite the right angle.
10. State the converse of Pythagoras theorem.
Solution
If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
11. If D, E, F are the respectively the midpoints of sides BC, CA and AB of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution
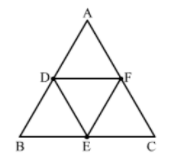
∴ DF || BC
And DF = 1/2BC
⇒ DF = BE
Since, the opposite sides of the quadrilateral are parallel and equal.
Hence, BDFE is a parallelogram
Similarly, DFCE is a parallelogram.
Now, in ∆ABC and ∆EFD
∠ABC = ∠EFD (Opposite angles of a parallelogram)
∠BCA = ∠EDF (Opposite angles of a parallelogram)
By AA similarity criterion, ∆ABC ~ ∆EFD
If two triangles are similar, then the ratio of their areas is equal to the squares of their corresponding sides.
∴ area(∆DEF)/area(∆ABC) = (DF/BC)2 = (DF/2 DF)2 = 1/4
Hence, the ratio of the areas of ∆DEF and ∆ABC is 1 : 4.
12. Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠A = 70°, PR = 9cm ∠P = 70° and PQ = 4.5 cm. Show that ΔABC ~ΔPQR and state that similarity criterion.
Solution
Now, In ∆ABC and ∆PQR
∠A = ∠P = 70° (Given)
AB/PQ = AC/PR [∵ 3/(4.5) = 6/9 ⇒ 1/1.5 = 1/1.5 ]
By SAS similarity criterion, ∆ABC~ ∆PQR
13. In ∆ABC~∆DEF such that 2AB = DE and BC = 6cm, find EF.
Solution
When two triangles are similar, then the ratios of the lengths of their corresponding sides are equal.
Here, ∆ABC ~∆DEF
∴ AB/DE = BC/EF
⇒ AB/(2 AB) = 6/EF
⇒ EF = 12 cm
14. In the given figure, DE║BC such that AD = x cm, DB = (3x + 4) cm, AE = (x + 3) cm and EC = (3x + 19) cm. Find the value of x.

In ∆ADE and ∆ABC
∠ADE = ∠ABC (Corresponding angles in DE ∥ BC)
∠AED = ∠ACB (Corresponding angles in DE ∥ BC)
By AA similarity criterion, ∆ADE ~ ∆ABC
If two triangles are similar, then the ratio of their corresponding sides are proportional
∴ AD/AB = AE/AC
⇒ AD/(AD + DB) = AE/(AE + EC)
⇒ x/(x + 3x + 4) = (x + 3)/(x + 3 + 3x + 19)
⇒ x/(4x + 4) = (x + 3)/(x + 3 + 3x + 19)
⇒ x/(2x + 2) = (x + 3)/(2x + 11)
⇒ 2x2 + 11x = 2x2 + 2x + 6x + 6
⇒ 3x = 6
⇒ x = 2
Hence, the value of x is 2.
15. A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
Solution
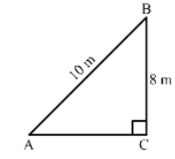
Now, In right triangle ABC
By using Pythagoras theorem, we have
AB2 = BC2 + CA2
⇒ 102 = 82 + CA2
⇒ CA2 = 100 – 64
⇒ CA2 = 36
⇒ CA = 6 m
Hence, the distance of the foot of the ladder from the base of the wall is 6 m.
16. Find the length of the altitude of an equilateral triangle of side 2a cm.
Solution
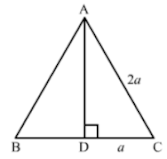
Suppose ABC is an equilateral triangle having AB = BC = CA = 2a.
Suppose AD is the altitude drawn from the vertex A to the side BC.
So, it will bisects the side BC
∴ DC = a
Now, In right triangle ADC
By using Pythagoras theorem, we have
AC2 = CD2 + DA2
⇒ (2a)2 = a2 + DA2
⇒ DA2 = 4a2 – a2
⇒ DA2 = 3a2
⇒ DA = √3
Hence, the length of the altitude of an equilateral triangle of side 2a cm is √3a cm.
17. ∆ABC~∆DEF such that ar(∆ABC) = 64 cm2and ar(∆DEF) = 169cm2. If BC = 4cm, find EF.
Solution
We have ∆ABC ~ ∆DEF
If two triangles are similar then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴ area(∆ABC)/area(∆DEF) = (BC/EF)2
⇒ 64/169 = (BC/EF)2
⇒ (8/13)2 = (4/EF)2
⇒ 8/13 = 4/EF
⇒ EF = 6.5 cm
18. In a trapezium ABCD, it is given that AB║CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that ar(∆AOB) = 84cm2. Find ar(∆COD).
Solution

∠ABO = ∠CDO (Alternate angles in AB ∥ CD)
∠AOB = ∠COD (Vertically opposite angles)
By AA similarity criterion, ∆AOB ~ ∆COD
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴ area(∆AOB)/area(∆COD) = (AB/CD)2
⇒ 84/area(∆COD) = (2CD/CD)2
⇒ area (∆COD) = 12 cm2
19. The corresponding sides of two similar triangles are in the ratio 2: 3. If the area of the smaller triangle is 48cm2, find the area of the larger triangle.
Solution
If two triangles are similar, then the ratio of their areas is equal to the squares of their corresponding sides.
∴ (area of smaller triangle)/(area of larger triangle) = (Side of smaller triangle)2/Side of larger triangle)
⇒ 48/(area of larger triangle = (2/3)2
⇒ area of larger triangle = 108 cm2
20. In an equilateral triangle with side a, prove that area = √3/4a2.
Solution

Suppose ABC is an equilateral triangle having AB = BC = CA = a.
Suppose AD is the altitude drawn from the vertex A to the side BC.
So, It will bisects the side BC
∴ DC = 1/2a
Now, In right triangle ADC
By using Pythagoras theorem, we have
AC2 = CD2 + DA2
⇒ a2 – (1/2.a)2 + DA2
⇒ DA2 = a2 – 1/4a2
⇒ DA2 = 3/4a2
⇒ DA = (√3/2)a
Now, area (∆ABC) = 1/2 × BC × AD
= 1/2 × a × √3/2.a
= √3/4.a2
21. Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Solution

We know that the diagonals of a rhombus perpendicularly bisect each other.
∴ ∠AOB = 900, AO = 12 cm and BO = 5 cm
Now, In right triangle AOB
By using Pythagoras theorem we have
AB2 = AO2 + BO2
= 122 + 52
= 144 + 25
= 169
∴ AB2 = 169
⇒ AB = 13 cm
Since, all the sides of a rhombus are equal.
Hence, AB = BC = CD = DA = 13 cm
22. Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57°. If ΔDEF ~ ΔGHK then find the measures of ∠F
Solution
If two triangles are similar then the corresponding angles of the two triangles are equal.
Here, ∆DEF ~ ∆GHK
∴ ∠E = ∠H = 57°
Now, In ∆ DEF
∠D + ∠E + ∠F = 180° (Angle sum property of triangle)
⟹ ∠F = 180° − 48° − 57° = 75°
23. In the given figure MN|| BC and AM: MB = 1: 2

Solution
We have
AM : MB = 1 : 2
⇒ MB/AM = 2/1
Adding 1 to both sides, we get
⇒ MB/AM + 1 = 2/1 + 1
⇒ (MB + AM)/AM = (2 + 1)/1
⇒ AB/AM = 3/1
Now, In ∆AMN and ∆ABC
∠AMN = ∠ABC (Corresponding angles in MN ∥ BC)
∠ANM = ∠ACB (Corresponding angles in MN ∥ BC)
By AA similarity criterion, ∆AMN ~ ∆ABC
If two triangles are similar, then the ratio of their areas is equal to the ratio of the squares of their corresponding sides.
∴ area(∆AMN)/area(∆ABC) = (AM/AB)2 = (1/3)2 = 1/9
24. In triangle BMP and CNR it is given that PB = 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP ~ CNR then find the perimeter of ΔCNR
Solution
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
Here, ∆BMP ~ ∆CNR
∴ BM/CN = BP/CR = MP/NR ...(1)
Now, BM/CN = MP/NR [Using (1)]
⇒ CN = (BM × NR)/MP = (9× 9)/6 = 13.5 cm
Again, BM/CN = BP/CR = [Using (1)]
⇒ CR = (BP × CN)/BM = (5 × 13.5)/9 = 7.5 cm
Perimeter of ∆CNR = CN + NR + CR = 13.5 + 9 + 7.5 = 30 cm
25. Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
Solution

We know that the altitude drawn from the vertex opposite to the non-equal side bisects the non-equal side.
Suppose ABC is an isosceles triangle having equal sides AB and BC.
So, the altitude drawn from the vertex will bisect the opposite side.
Now, In right triangle ABD
By using Pythagoras theorem, we have
AB2 = BD2 + DA2
⇒ 252 = 72 + DA2
⇒ DA2 = 625 − 49
⇒ DA2 = 576
⇒ DA = 24 cm
26. A man goes 12m due south and then 35m due west. How far is he from the starting point.
Solution

By using Pythagoras theorem, we have
OW2 = WS2 + SO2
= 352 + 122
= 1225 + 144
= 1369
∴ OW2 = 1369
⇒ OW = 37 m
Hence, the man is 37 m away from the starting point.
27. If the lengths of the sides BC, CA and AB of a ΔABC are a, b and c respectively and AD is the bisector ∠A then find the lengths of BD and DC
Solution
Let DC = x
∴ BD = a - x
By using angle bisector there in ∆ABC, we have
AB/AC = BD/DC
⇒ c/b = (a – x)/x
⇒ cx = ab – bx
⇒ x(b + c) = ab
⇒ x = ab/(b + c)
Now, a – x = a – ab/(b + c)
= (ab + ac – ab)/(b + c)
= ac/(a + b)
28. In the given figure, ∠AMN = ∠MBC = 76°. If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN of terms of P, q and r.

In ∆AMN and ∆ABC
∠AMN = ∠ABC = 76° (Given)
∠A = ∠A (Common)
By AA similarity criterion, ∆AMN ~ ∆ABC
If two triangles are similar, then the ratio of their corresponding sides are proportional
∴ AM/AB = MN/BC
⇒ AM/(AM + MB) = MN/BC
⇒ a/(a + b) = MN/c
⇒ MN = ac/(a + b)
29. Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
Solution

We know that the diagonals of a rhombus perpendicularly bisect each other.
∴ ∠AOB = 90°, AO = 20 cm and BO = 21 cm
Now, In right triangle AOB
By using Pythagoras theorem we have
AB2 = AO2 + OB2
= 202 + 212
= 400 + 441
= 841
∴ AB2 = 841
⇒ AB = 29 cm
Since, all the sides of a rhombus are equal.
Hence, AB = BC = CD = DA = 29 cm
30. For each of the following statements state whether true(T) or false (F)
(i) Two circles with different radii are similar.
(ii) any two rectangles are similar
(iii) if two triangles are similar then their corresponding angles are equal and their corresponding sides are equal
(iv) The length of the line segment joining the midpoints of any two sides of a triangles is equal to half the length of the third side.
(v) In a ΔABC, AB = 6 cm, ∠A = 45°and AC = 8 cm and in a ΔDEF, DF = 9 cm ∠D = 45° and DE = 12 cm then ΔABC ~ ΔDEF .
(vi) the polygon formed by joining the midpoints of the sides of a quadrilateral is a rhombus.
(vii) the ratio of the perimeter of two similar triangles is the same as the ratio of the their corresponding medians.
(ix) if O is any point inside a rectangle ABCD then OA2 + OC2 = OB2 + OD2
(x) The sum of the squares on the sides of a rhombus is equal to the sum of the squares on its diagonals.
Solution
(i) Two rectangles are similar if their corresponding sides are proportional.
(ii) True
Two circles of any radii are similar to each other.
(iii) false
If two triangles are similar, their corresponding angles are equal and their corresponding sides are proportional.
(iv) True
Suppose ABC is a triangle and M, N are

Construction: DE is expanded to F such that EF = DE
To proof = DE = 1/2 BC
Proof: In ∆ADE and ∆CEF
AE = EC (E is the mid point of AC)
DE = EF (By construction)
AED = CEF (Vertically Opposite angle)
By SAS criterion, ∆ADE ~ ∆CEF
CF = AD (CPCT)
⇒ BD = CF
∠ADE = ∠EFC (CPCT)
Since, ∠ADE and ∠EFC are alternate angle
Hence, AD ‖ CF and BD ‖ CF
When two sides of a quadrilateral are parallel, then it is a parallelogram
∴ DF = BC and BD ‖ CF
∴ BDFC is a parallelogram
Hence, DF = BC
⇒ DE + EF = BC
⇒ DE = 1/2.BC
(v) False
In ∆ABC, AB = 6 cm, ∠A = 450 and AC = 8 cm and in ∆DEF, DF = 9 cm, ∠D = 45° and DE = 12 cm, then ∆ABC ~ ∆DEF.
In ∆ABC and ∆DEF
(vi) False
The polygon formed by joining the mid points of the sides of a quadrilateral is a parallelogram.
(vii) True

Given: ∆ABC ~ ∆DEF
To prove = Ar(∆ABC)/Ar(∆DEF) = (AP/DQ)2
Proof: in ∆ABP and ∆DEQ
∠BAP = ∠EDQ (As ∠A = ∠D, so their Half is also equal)
∠B = ∠E (∠ABC ~ ∆DEF)
By AA criterion, ∆ABP and ∆DEQ
AB/DE = AP/DQ …(1)
Since, ∆ABC ~ ∆DEF
∴ Ar(∆ABC)/Ar(∆DEF) = (AB/DE)2
⇒ Ar(∆ABC)/Ar(∆DEF) = (AP/DQ)2 [Using (1)]
(viii)

To Prove = (Perimeter(∆ABC)/Perimeter(∆DEF) = AP/DQ
Proof: In ∆ABP and ∆DEQ
∠B = ∠E (∴∆ABC ~ ∆DEF)
∴ ∆ABC ~ ∆DEF
∴ AB/DE = BC/EF
⇒ AB/DE = 2BP/2EQ
⇒ AB/DE = BP/EQ
By SAS criterion, ∆ABP ~ ∆DEQ
AB/DE = AP/DQ ...(1)
Since, ∆ABC ~ ∆DEF
∴ Perimeter(∆ABC)/(Perimeter(∆DEF) = AB/DE
⇒ Perimeter(∆ABC)/Perimeter(∆DEF) = AP/DQ [Using (1)]
(ix) True

Suppose ABCD is a rectangle with O is any point inside it.
Construction: OA2 + OC2 = OB2 + OD2
Proof:
OA2 + OC2 = (AS2 + OS2) + (OQ2 + QC2) [Using Pythagoras theorem in right triangle AOP and COQ]
= (BQ2 + OS2) + (OQ2 + DS2)
= (BQ2 + OQ2) + (OS2 + DS2) [Using Pythagoras theorem in right triangle BOQ and DOS]
= OB2 + OD2
Hence, LHS = RHS
(x) True
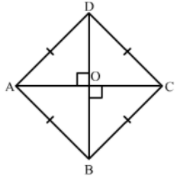
Suppose ABCD is a rhombus having AC and BD its diagonals.
Since, the diagonals of a rhombus perpendicular bisect each other.
Hence, AOC is a right angle triangle
In right triangle AOC
By using Pythagoras theorem, we have
AB2 = (AC/2)2 + (BD/2)2
[∴ Diagonals of a rhombus perpendicularly bisect each other]
⇒ AB2 = (AC/2)2 + (BD/2)2
⇒ 4AB2 = AC2 + BD2
⇒ AB2 + AB2 + AB2 + AB2 = AC2 + BD2
⇒ AB2 + BC2 + CD2 + DA2 = AC2 + BD2 [∵ All sides of a rhombus are equal]
