RS Aggarwal Solutions Chapter 4 Triangles Exercise - 4B Class 10 Maths
Chapter Name | RS Aggarwal Chapter 4 Triangles |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 4B Solutions
1. In each of the given pairs of triangles, find which pairs of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
(i)
(i) We have:°
∠BAC = ∠PQR = 50°
∠ABC = ∠QPR = 60°
∠ACB = ∠PRQ = 70°
Therefore, by AAA similarity theorem, ∆ABC – QPR
(ii) We have:
AB/DF = 3/6 = 1/2 and BC/DE = 4.5/9 = 1/2
But, ∠ABC ≠ ∠EDF (Included angles are not equal)
Thus, this triangles are not similar.
(iii) We have:
CA/QR = 8/6 = 4/3 and CB/PQ = 6/4.5 = 4/3
⇒ CA/QR = CB/PQ
Also, ∠ACB = ∠PQR = 80°
Therefore, by SAS similarity theorem, ∆ACB - ∆RQP.
(iv) We have
DE/QR = 2.5/5 = 1/2
EF/PQ = 2/4 = 1/2
DF/PR = 3/6 = 1/2
⇒ DE/QR = EF/PQ = DF/PR
Therefore, by SSS similarity theorem, ∆FED - ∆PQR
(v) In ∆ ABC,
∠A + ∠B + ∠C = 180° (Angle Sum Property)
⇒ 80° + ∠B + 70° = 180°
⇒ ∠B = 30°
∠A = ∠M and ∠B = ∠N
Therefore, by AA similarity, ∆ABC - ∆MNR
2. In the given figure, ∆ODC~∆OBA, ∠BOC = 115° and ∠CDO = 70°.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.
(i) It is given that DB is a straight line.
Therefore,
∠DOC + ∠COB = 180°
∠DOC = 180° − 115° = 65°
(ii) In ∆ DOC, we have:
∠ODC + ∠DCO + ∠DOC = 180°
Therefore,
70° + ∠DCO + 65° = 180°
∠DCO = 180° − 70° − 65° = 45°
(iii) It is given that ∆ODC - ∆OBA
Therefore,
∠OAB = ∠OCD = 45°
(iv) Again, ∆ODC - ∆OBA
Therefore,
∠OBA = ∠ODC = 70°
3. In the given figure, ∆OAB ~ ∆OCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
Solution(i) Let OA be X cm.
∵ ∆OAB - ∆OCD
∴ OA/OC = AB/CD
⇒ x/3.5 = 8/5
⇒ x = (8 × 3.5)/5 = 5.6
Hence, OA = 5.6 cm
(ii) Let OD be Y cm
∵ ∆ OAB - ∆ OCD
∴ AB/CD = OB/OD
⇒ 8/5 = 6.4/y
⇒ y = (6.4 × 5)/8 = 4
Hence, DO = 4 cm
4. In the given figure, if ∠ADE = ∠B, show that ∆ADE ~ ∆ABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
SolutionGiven :
∠ADE = ∠ABC and ∠A = ∠A
Let DE be X cm
Therefore, by AA similarity theorem, ∆ADE - ∆ABC
⇒ AD/AB = DE/BC
⇒ 3.8/(3.6 + 2.1) = x/4.2
⇒ x = (3.8 × 4.2)/5.7 = 2.8
Hence, DE = 2.8 cm
5. The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
Solution
It is given that triangles ABC and PQR are similar.
Therefore,
Perimeter(∆ABC)/Perimeter of (∆PQR) = AB/PQ
⇒ 32/24 = AB/12
⇒ AB = (32 × 12)/24 = 16 cm
6. The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the perimeter of ∆DEF is 25cm, find the perimeter of ∆ABC.
Solution
It is given that ∆ABC - ∆DEF.
Therefore, their corresponding sides will be proportional.
Also, the ratio of the perimeters of similar triangles is same as the ratio of their corresponding sides.
⇒ Perimeter of ∆ABC/Perimeter of ∆DEF = BC/EF
Let the perimeter of ∆ABC be X cm
Therefore,
x/25 = 9.1/6.5
⇒ x = (9.1 × 25)/6.5
Thus, the perimeter of ∆ABC is 35 cm.
7. In the given figure, ∠CAB = 90° and AD⊥BC. Show that ∆BDA ~ ∆BAC. If AC = 75cm, AB = 1m and BC = 1.25m, find AD.
SolutionIn ∆ BDA and ∆ BAC, we have:
∠BDA = ∠BAC = 90°
∠DBA = ∠CBA (Common)
Therefore, by AA similarity theorem, ∆BDA - ∆BAC
⇒ AD/AC = AB/BC
⇒ AD/0.75 = 1/(1.25)
⇒ AD = 0.75/1.25
= 0.6 m or 60 cm
8. In the given figure, ∠ABC = 90° and BD⊥AC.
If AB = 5.7cm, BD = 3.8cm and CD = 5.4cm, find BC.
SolutionIt is given that ABC is a right angled triangle and BD is the altitude drawn from the right angle to the hypotenuse.
In ∆ BDC and ∆ ABC, we have :
∠ABC = ∠BBC = 90° (Given)
∠C = ∠C (Common)
By AA similarity theorem, we get:
∆ BDC- ∆ ABC
AB/BD = BC/DC
⇒ 5.7/3.8 = BC/5.4
⇒ BC = (5.7/3.8 × 5.4)
= 8.1
Hence, BC = 8.1 cm
9. In the given figure, ∠ABC = 90° and BD⊥AC.
If BD = 8cm, AD = 4cm, find CD.
SolutionIt is given that ABC is a right angled triangle
and BD is the altitude drawn from the right angle to the hypotenuse.
In ∆ DBA and ∆ DCB, we have:
∠BDA = ∠CDB
∠DBA = ∠DCB = 90°
Therefore, by AA similarity theorem, we get:
∆DBA - ∆DCB
⇒ BD/CD = AD/BD
⇒ CD = BD2/AD
CD = (8 × 8)/4 = 16 cm
10. P and Q are points on the sides AB and AC respectively of a ∆ABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
Solution
We have:
AP/AB = 2/6 = 1/3 and AQ/AC = 3/9 = 1/3
⇒ AP/AB = AQ/AC
In ∆APQ and ∆ABC, we have:
AP/AB = AQ/AC
∠A = ∠A
Therefore, by AA similarity theorem, we get: ∆APQ - ∆ABC
Hence, PQ/BC = AQ/AC = 1/3
⇒ PQ/BC = 1/3
⇒ BC = 3PQ
This completes the proof.
11. ABCD is parallelogram and E is a point on BC.
If the diagonal BD intersects AE at F, prove that
AF × FB = EF × FD.
SolutionWe have:
∠AFD = ∠EFB (Vertically Opposite angles)
∵ DA || BC
∴ ∠DAF = ∠BEF (Alternate angles)
∆ DAF ~ ∆ BEF (AA similarity theorem)
⇒ AF/EF = FD/FB
Or, AF × FB = FD × EF
This completes the proof.
12. In the given figure, DB⊥BC, DE⊥AB and AC⊥BC.
Prove that BE/DE = AC/BC
SolutionIn ∆BED and ∆ACB, we have:
∠BED = ∠ACB = 90°
∵ ∠B + ∠C = 180°
∴ BD || AC
∠EBD = ∠CAB (Alternate angles)
Therefore, by AA similarity theorem, we get:
∆BED ~ ∆ACB
⇒ BE/AC = DE/BC
⇒ BE/DE = AC/BC
This completes the proof.
13. A vertical pole of length 7.5 cm casts a shadow 5m long on the ground and at the same time a tower casts a shadow 24m long. Find the height of the tower.
Solution
Let AB be the vertical stick and BC be its shadow.
Given:
AB = 7.5 m, BC = 5 m
Let PQ be the tower and QR be its shadow.
Given:
QR = 24 m
Let the length of PQ be x m.
In ∆ ABC and ∆ PQR, we have:
∠ABC = ∠PQR = 90°
∠ACB = ∠PRQ (Angular elevation of the Sun at the same time)
Therefore, by AA similarity theorem, we get:
∆ABC ~ ∆PQR
⇒ AB/BC = PQ/QR
⇒ 7.5/5 = x/24
x = 7.5/5 × 24 = 36 cm
Therefore, PQ = 36 m
Hence, the height of the tower is 36 m.
14. In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2.
Prove that ∆ACP ~ ∆BCQ.
SolutionDisclaimer: It should be ∆APC ~ ∆BCQ instead of ∆ACP ~ ∆BCQ
It is given that ∆ABC is an isosceles triangle.
Therefore,
CA = CB
⇒ ∠CAB = ∠CBA
⇒ 180° - ∠CAB = 180° − ∠CBA
⇒ ∠CAP = ∠CBQ
Also,
AP × BQ = AC2
⇒ AP/AC = AC/BQ
⇒ AP/AC = BC/BQ (∵ AC = BC)
Thus, by SAS similarity theorem, we get
∆APC ~ ∆BCQ
This completes the proof.
15. In the given figure, ∠1 = ∠2 and AC/BD = CB/CE.
Prove that ∆ACB ~ ∆DCE.
We have:
∠1 = ∠2
Also, ∠1 = ∠2
i.e., ∠DBC = ∠ACB
Therefore, by SAS similarity theorem, we get :
∆ACB - ∆DCE
16. ABCD is a quadrilateral in which AD = BC.
If P, Q, R, S be the midpoints of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
SolutionIn ∆ ABC, P and Q are mid points of AB and AC respectively.
So, PQ || BC and PQ = 1/2BC …(1)
Similarly in ∆ADC,
QR = 1/2 AD = 1/2 BC …(2)
Now in ∆BCD,
SR = 1/2BC ...(3)
Similarly in ∆ABD,
PS = 1/2AD = 1/2BC ...(4)
Using (1), (2), (3), and (4).
PQ = QR = SR = PS
Since, all sides are equal
Hence, PQRS is a rhombus.
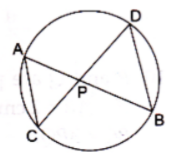
17. In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ~ ΔPDB
(b) PA.PB = PC.PD
Solution
Given: AB and CD are two chords
To Prove:
(a) ∆ PAC ~ ∆PDB
(b) PA.PB = PC.PD
Proof: In ∆ PAC and ∆ PDB
∠APC = ∠DPB (Vertically Opposite angles)
∠CAP = ∠BDP (Angles in the same segment are equal)
By AA similarity criterion ∆PAC ~ ∆PDB
When two triangles are similar, then the ratios of lengths of their corresponding sides are proportional.
∴ PA/PD = PC/PB
⇒ PA. PB = PC. PD
18. Two chords AB and CD of a circle intersect at a point P outside the circle. Prove that:
(i) ∆ PAC ~ ∆ PDB
(ii) PA. PB = PC.PD
SolutionGiven : AB and CD are two chords
To Prove:
(a) ∆PAC - ∆PDB
(b) PA. PB = PC.PD
Proof: ∠ABD + ∠ACD = 180°...(1) (Opposite angles of a cyclic quadrilateral are supplementary)
∠PCA + ∠ACD = 180°...(2) (Linear Pair Angles)
Using (1) and (2), we get
∠ABD + ∠PCA
∠A = ∠A (Common)
By AA similarity-criterion ∆PAC - ∆PDB
When two triangles are similar, then the rations of the lengths of their corresponding sides are proportional.
∴ PA/PD = PC/PB
⇒ PA.PB = PC.PD
19. In a right triangle ABC, right angled at B, D is a point on hypotenuse such that BD ⊥ AC, if DP⊥ AB and DQ ⊥ BC then prove that
(a) DQ2 = DP.QC
(b) DP2 = DQ AP2
Solution
We know that if a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then the triangles on the both sides of the perpendicular are similar to the whole triangle and also to each other.
(a) Now using the same property in In ∆BDC, we get
∆CQD ~ ∆DQB
CQ/DQ = DQ/QB
⇒ DQ2 = QB.CQ
Now, Since all the angles in quadrilateral BQDP are right angles.
Hence, BQDP is a rectangle.
So, QB = DP and DQ = PB
∴ DQ2 = DP.CQ
(b) Similarly, ∆APD ~ ∆DPB
AP/DP = PD/PB
⇒ DP2 = AP. PB
⇒ DP2 = AP. DQ [∵ DQ = PB]