RS Aggarwal Solutions Chapter 3 Linear Equations in Two Variables Exercise - 3A Class 10 Maths
Chapter Name | RS Aggarwal Chapter 3 Linear Equations in Two Variables |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 3A Solutions
1. Solve the system of equations graphically:
2x + 3y = 2,
x – 2y = 8
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' representing the x axis and y-axis, respectively.
Graph of 2x + 3y = 2
2x + 3y = 2
⇒ 3y = (2 – 2x)
⇒ 3y = 2(1 – x)
⇒ y = 2(1 – x)/3 …(i)
Putting x = 1, we get y = 0
Putting x = -2, we get y = 2
Putting x = 4, we get y = -2
Thus, we have the following table for the equation 2x + 3y = 2
| x | 1 | -2 | 4 |
| y | 0 | 2 | -2 |
Join AB and AC to get the graph line BC. Extend it on both ways.
Thus, the line BC is the graph of 2x + 3y = 2.
Graph of x - 2y = 8
x – 2y = 8
⇒ 2y = (x – 8)
⇒ y = (x – 8)/2 …(ii)
Putting x = 2, we get y = -3
Putting x = 4, we get y = -2
Putting x = 0, we get y = -4
Thus, we have the following table for the equation x – 2y = 8.
| x | 2 | 4 | 0 |
| y | -3 | -2 | -4 |
Join PQ and QC and extend it on both ways.
Thus, line PC is the graph of x – 2y = 8.
The two graph lines intersect at C(4, -2).
∴ x = 4 and y = -2 are the solutions of the given system of equations.
2. Solve the system of equations graphically:
3x + 2y = 4,
2x – 3y = 7
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' representing the x axis and y-axis, respectively.
Graph of 3x + 2y = 4
3x + 2y = 4
⇒2y = (4 – 3x)
⇒ y = (4 – 3x)/2 …(i)
Putting x = 0, we get y = 2
Putting x = 2, we get y = -1
Putting x = -2, we get y = 5
Thus, we have the following table for the equation 3x + 2y = 4
| x | 0 | 2 | -2 |
| y | 2 | -1 | 5 |
Join AB and AC to get the graph line BC. Extend it on both ways.
Thus, BC is the graph of 3x + 2y = 4.
Graph of 2x - 3y = 7
2x – 3y = 7
⇒ 3y = (2x – 7)
⇒ y = (2x – 7)/3 …(ii)
Putting x = 2, we get y = -1
Putting x = -1, we get y = -3
Putting x = 5, we get y = 1
Thus, we have the following table for the equation 2x – 3y = 7.
| x | 2 | -1 | 5 |
| y | -1 | -3 | 1 |
Thus, line PQ is the graph of 2x – 3y = 7.
The two graph lines intersect at B(2, -1).
∴ x = 2 and y = -1 are the solutions of the given system of equations.
3. Solve the system of equations graphically:
2x + 3y = 8,
x – 2y + 3 = 0
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 2x + 3y = 8
2x + 3y = 8
⇒ 3y = (8 – 2x)
⇒ y = (8 – 2x)/3 …(i)
Putting x = 1, we get y = 2.
Putting x = -5, we get y = 6.
Putting x = 7, we get y = -2.
Thus, we have the following table for the equation 2x + 3y = 8.
| x | 1 | -5 | 7 |
| y | 2 | 6 | -2 |
Join AB and AC to get the graph line BC. Extend it on both ways.
Thus, BC is the graph of 2x + 3y = 8.
Graph of x - 2y + 3 = 0
x – 2y + 3 = 0
⇒ 2y = (x + 3)
⇒ y = (x + 3)/2 …(ii)
Putting x = 1, we get y = 2.
Putting x = 3, we get y = 3.
Putting x = -3, we get y = 0.
Thus, we have the following table for the equation x – 2y + 3 = 0.
| x | 1 | 3 | -3 |
| y | 2 | 3 | 0 |
Thus, PQ is the graph of x – 2y + 3 = 0.
The two graph lines intersect at A (1, 2).
∴ x = 1 and y = 2.
4. Solve the system of equations graphically:
2x - 5y + 4 = 0,
2x + y - 8 = 0
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 2x - 5y + 4 = 0
2x – 5y + 4 = 0
⇒ 5y = (2x + 4)
⇒ y = (2x + 4)/5 …(i)
Putting x = -2, we get y = 0.
Putting x = 3, we get y = 2.
Putting x = 8, we get y = 4.
Thus, we have the following table for the equation 2x - 5y + 4 = 0.
| x | -2 | 3 | 8 |
| y | 0 | 2 | 4 |
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of 2x - 5y + 4 = 0.
Graph of 2x + y - 8 = 0
2x + y - 8 = 0
⇒ y = (8 – 2x) …(ii)
Putting x = 1, we get y = 6.
Putting x = 3, we get y = 2.
Putting x = 2, we get y = 4.
Thus, we have the following table for the equation 2x + y - 8 = 0.
| x | 1 | 3 | 2 |
| y | 6 | 2 | 4 |
Now, plot the points P (1, 6) and Q (2, 4). The point B (3, 2) has already been plotted. Join PQ and QB and extend it on both ways.
Thus, PB is the graph of 2x + y - 8 = 0.
The two graph lines intersect at B (3, 2).
∴ x = 3 and y = 2
5. Solve the system of equations graphically:
3x + 2y = 12,
5x – 2y = 4
Solution
The given equations are:
3x + 2y = 12 ...(i)
5x – 2y = 4 ...(ii)
From (i), write y in terms of x
y = (12 – 3x) ...(iii)
Now, substitute different values of x in (iii) to get different values of y
For x = 0, y = (12 – 3x)/2 = (12 – 0)/2 = 6
For x = 2, y = (12 – 3x)/2 = (12 – 6)/2 = 3
For x = 4, y = (12 – 3x)/2 = (12 – 12)/2 = 0
Thus, the table for the first equation (3x + 2y = 12) is
| x | 0 | 2 | 4 |
| y | 6 | 3 | 0 |
Now, plot the points A (0, 6), B (2, 3) and C (4, 0) on a graph paper and join A, B and C to get the graph of 3x + 2y = 12.
From (ii), write y in terms of x
y = (5x - 4)/2 ….(iv)
Now, substitute different values of x in (iv) to get different values of y
For x = 0, y = (5x – 4)/2 = (0 – 4)/2 = - 2
For x = 2, y = (5x – 4)/2 = (10 – 4)/2 = 3
For x = 4, y = (5x – 4)/2 = (20 – 4)/2 = 8
Thus, the table for the first equation (5x – 2y = 4) is
| x | 0 | 2 | 4 |
| y | -2 | 3 | 8 |
Now, plot the points D (0, -2), E (2, 3) and F (4, 8) on the same graph paper and join D, E and F to get the graph of 5x – 2y = 4.
From the graph it is clear that, the given lines intersect at (2, 3).
Hence, the solution of the given system of equations is (2, 3).
6. Solve the system of equations graphically:
3x + y + 1 = 0,
2x - 3y + 8 = 0
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 3x + y + 1 = 0
3x + y + 1 = 0
⇒ y = (-3x - 1) …(i)
Putting x = 0, we get y = -1.
Putting x = -1, we get y = 2.
Putting x = 1, we get y = -4.
Thus, we have the following table for the equation 3x + y + 1 = 0.
| x | 0 | -1 | 1 |
| y | -1 | 2 | -4 |
Now, plot the points A(0, -1), B(-1, 2) and C(1, -4) on the graph paper.
Join AB and AC to get the graph line BC. Extend it on both ways.
Thus, BC is the graph of 3x + y + 1 = 0.
Graph of 2x - 3y + 8 = 0
2x - 3y + 8 = 0
⇒ 3y = (2x + 8)
∴ y = (2x + 8)/3
Putting x = -1, we get y = 2.
Putting x = 2, we get y = 4.
Putting x = -4, we get y = 0.
Thus, we have the following table for the equation 2x - 3y + 8 = 0.
| x | -1 | 2 | -4 |
| y | 2 | 4 | 0 |
Thus, PQ is the graph of 2x + y - 8 = 0.
The two graph lines intersect at B (-1, 2).
∴ x = -1 and y = 2
7. Solve the system of equations graphically:
2x + 3y + 5 = 0,
3x – 2y – 12 = 0
Solution
From the first equation, write y in terms of x
y = − (5 + 2x)/3 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -1, y = (5 – 2)/3 = - 1
For x = 2, y = -(5 + 4)/3
For x = 5, y = -(5 + 10)/3 = - 5
Thus, the table for the first equation (2x + 3y + 5 = 0) is
| x | -1 | 2 | 5 |
| y | -1 | -3 | -5 |
Now, plot the points A (-1, -1), B (2, -3) and C (5, -5) on a graph paper and join them to get the graph of 2x + 3y + 5 = 0.
From the second equation, write y in terms of x
y = (3x – 12)/2 ...(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = (0 – 12)/2 = -6
For x = 2, y = (6 – 12)/2 = -3
For x = 4, y = (12 – 12)/2 = 0
So, the table for the second equation (3x – 2y – 12 = 0) is
| x | 0 | 2 | 4 |
| y | -6 | -3 | 0 |
From the graph it is clear that, the given lines intersect at (2, -3).
Hence, the solution of the given system of equation is (2, -3).
8. Solve the system of equations graphically:
2x – 3y + 13 = 0,
3x – 2y + 12 = 0
Solution
From the first equation, write y in terms of x
y = (2x + 13)/3 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -5, y = (-10 + 13)/3 = 1
For x = 1, y = (2 + 13)/3 = 5
For x = 4, y = (8 + 13)/3 = 7
Thus, the table for the first equation (2x - 3y + 13 = 0) is
| x | -5 | 1 | 4 |
| y | 1 | 5 | 7 |
Now, plot the points A (-5, 1), B (1, 5) and C (4, 7) on a graph paper and join A, B and C to get the graph of 2x - 3y + 13 = 0.
From the second equation, write y in terms of x
y = (3x + 12)/2 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -4, y = (-12 + 12)/2 = 0
For x = -2, y = (-6 + 12)/2 = 3
For x = 0, y = (0 + 12)/2 = 6
So, the table for the second equation (3x – 2y + 12 = 0) is
| x | -4 | -2 | 0 |
| y | 0 | 3 | 6 |
Hence, the solution of the given system of equation is (-2, 3).
9. Solve the system of equations graphically:
2x + 3y = 4,
3x – y = -5
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 2x + 3y = 4
2x + 3y = 4
⇒ 3y = (4 – 2x)
∴ y = (4 – 2x)/3 …(i)
Putting x = -1, we get y = 2.
Putting x = 2, we get y = 0.
Putting x = 5, we get y = -2.
Thus, we have the following table for the equation 2x + 3y = 4.
| x | -1 | 2 | 5 |
| y | 2 | 0 | -2 |
Now, plot the points A (-1, 2), B (2, 0) and C(5, -2) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of 2x + 3y = 4.
Graph of 3x – y = -5
3x – y = -5
⇒ y = (3x + 5) …..(ii)
Putting x = -1, we get y = 2.
Putting x = 0, we get y = 5.
Putting x = -2, we get y = -1.
Thus, we have the following table for the equation 3x – y = -5.
| x | -1 | 0 | -2 |
| y | 2 | 5 | -1 |
Now, plot the points P (0, 5) and Q (-2, -1). The point A (-1, 2) has already been plotted.
Join PA and QA and extend it on both ways.
Thus, PQ is the graph of 3x - y = - 5.
∴ x = -1 and y = 2 are the solutions of the given system of equations.
10. Solve the system of equations graphically:
x + 2y + 2 = 0
3x + 2y - 2 = 0
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 2x + 3y = 4
x + 2y + 2 = 0
⇒ 2y = (–2 – x)
∴ y = (-2 - x)/2 …(i)
Putting x = -2, we get y = 0.
Putting x = 0, we get y = -1.
Putting x = 2, we get y = -2.
Thus, we have the following table for the equation x + 2y + 2 = 0.
| x | -2 | 0 | 2 |
| y | 0 | -1 | -2 |
Now, plot the points A (-2, 0), B (0, -1) and C (2, -2) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of x + 2y + 2 = 0.
Graph of 3x + 2y - 2 = 0
3x + 2y – 2 = 0
⇒ 2y = (2 – 3x)
∴ y = (2 – 3x)/2 ...(ii)
Putting x = 0, we get y = 1.
Putting x = 2, we get y = -2.
Putting x = 4, we get y = -5.
Thus, we have the following table for the equation 3x + 2y – 2 = 0.
| x | 0 | 2 | 4 |
| y | 1 | -2 | -5 |
Now, plot the points P (0, 1) and Q(4, -5). The point C(2, -2) has already been plotted.
Join PC and QC and extend it on both ways.
Thus, PQ is the graph of 3x + 2y – 2 = 0.
The two graph lines intersect at A(2, -2).
∴ x = 2 and y = -2.
11. Solve graphically the system of equations
x – y – 3 = 0
2x – 3y – 4 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Solution
From the first equation, write y in terms of x
y = x + 3 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -3, y = -3 + 3 = 0
For x = -1, y = -1 + 3 = 2
For x = 1, y = 1 + 3 = 4
Thus, the table for the first equation (x - y + 3 = 0) is
| x | -3 | -1 | 1 |
| y | 0 | 2 | 4 |
Now, plot the points A(-3, 0), B(-1, 2) and C(1, 4) on a graph paper and join A, B and C to get the graph of x - y + 3 = 0.
From the second equation, write y in terms of x
y = (4 – 2x)/3 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -4, y = (4 + 8)/3 = 4
For x = -1, y = (4 + 12)/3 = 2
For x = 2, y = (4 – 4)/3 = 0
So, the table for the second equation (2x + 3y - 4 = 0) is
| x | -4 | -1 | 2 |
| y | 4 | 2 | 0 |
Now, plot the points D(-4, 4), E(-1, 2) and F(2, 0) on the same graph paper and join D, E and F to get the graph of 2x + 3y - 4 = 0.
So, the solution of the given system of equation is (-1, 2).
The vertices of the triangle formed by the given lines and the x-axis are (-3, 0), (-1, 2) and (2, 0).
Now, draw a perpendicular from the intersection point E on the x-axis. So,
Area (∆EAF) = 1/2 × AF × EM
= 1/2 × 5 × 2
= 5 sq. units
Hence, the vertices of the triangle formed by the given lines and the x-axis are (-3, 0), (-1, 2) and (2, 0) and its area is 5 sq. units.
12. Solve graphically the system of equations
2x – 3y + 4 = 0
x + 2y – 5 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the x-axis.
Solution
From the first equation, write y in terms of x
y = (2x + 4) ….(i)
Substitute different values of x in (i) to get different values of y
For x = -2, y = -(4 + 4)/3 = 0
For x = 1, y = (2 + 4)/3 = 2
For x = 4, y = (8 + 4)/3 = 4
Thus, the table for the first equation (2x - 3y + 4 = 0) is
| x | -2 | 1 | 4 |
| y | 0 | 2 | 4 |
Now, plot the points A(-2, 0), B(1, 2) and C(4, 4) on a graph paper and join A, B and C to get the graph of 2x - 3y + 4 = 0.
From the second equation, write y in terms of x
y = (5 – x)/2 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -3, y = (5 + 3)/2 = 4
For x = 1, y = (5 – 1)/2 = 2
For x = 5, y = (5 – 5)/2 = 0
So, the table for the second equation (x + 2y - 5 = 0) is
| x | -3 | 1 | 5 |
| y | 4 | 2 | 0 |
Now, plot the points D(-3, 4), B(1, 2) and F(5, 0) on the same graph paper and join D, E and F to get the graph of x + 2y - 5 = 0.
From the graph, it is clear that, the given lines intersect at (1, 2).
So, the solution of the given system of equation is (1, 2).
From the graph, the vertices of the triangle formed by the given lines and the x-axis are (-2, 0), (1, 2) and (5, 0).
Now, draw a perpendicular from the intersection point B on the x-axis. So,
Area (∆BAF) = 1/2 × AF × BM
= 1/2 × 7 × 2
= 7 sq. units
Hence, the vertices of the triangle formed by the given lines and the x-axis are (-2, 0), (1, 2) and (5, 0) and the area of the triangle is 7 sq. units.
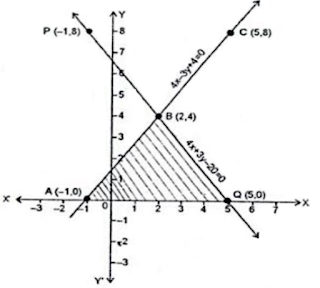
13. Solve the following system of linear equations graphically
4x – 3y + 4 = 0, 4x + 3y – 20 = 0.
Find the area of the region bounded by these lines and the x-axis.
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 4x - 3y + 4 = 0
4x - 3y + 4 = 0
⇒ 3y = (4x + 4)
∴ y = (4x + 4)/3 ...(i)
Putting x = -1, we get y = 0.
Putting x = 2, we get y = 4.
Putting x = 5, we get y = 8.
Thus, we have the following table for the equation 4x - 3y + 4 = 0.
|
x |
-1 |
2 |
5 |
|
y |
0 |
4 |
8 |
Now, plot the points A(-1, 0), B(2, 4) and C(5, 8) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of 4x - 3y + 4 = 0.
Graph of 4x + 3y - 20 = 0
4x + 3y - 20 = 0
⇒ 3y = (–4x + 20)
∴ y = (-4x + 20)/3 ...(ii)
Putting x = 2, we get y = 4.
Putting x = -1, we get y = 8.
Putting x = 5, we get y = 0.
Thus, we have the following table for the equation 4x + 3y - 20 = 0.
|
x |
2 |
-1 |
5 |
|
y |
4 |
8 |
0 |
Now, plot the points P(1, -8) and Q(5, 0). The point B(2, 4) has already been plotted. Join PB and QB to get the graph line. Extend it on both ways.
Then, line PQ is the graph of the equation 4x + 3y - 20 = 0.
The two graph lines intersect at B(2, 4).
∴ The solution of the given system of equations is x = 2 and y = 4.
Clearly, the vertices of ∆ABQ formed by these two lines and the x-axis are Q(5, 0), B(2, 4) and A(-1, 0).
Now, consider ∆ABQ.
Here, height = 4 units and base (AQ) = 6 units
∴ Area ∆ABQ = 1/2 × base × height sq. units
= 1/2 × 6 × 4
= 12 sq. units.
14. Solve the following system of linear equations graphically
x – y + 1 = 0, 3x + 2y – 12 = 0.
Calculate the area bounded by these lines and the x-axis.
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of x - y + 1 = 0
x - y + 1 = 0
⇒ y = x + 1 …(i)
Putting x = -1, we get y = 0.
Putting x = 1, we get y = 2.
Putting x = 2, we get y = 3.
Thus, we have the following table for the equation x - y + 1 = 0.
|
x |
-1 |
1 |
2 |
|
y |
0 |
2 |
3 |
Now, plot the points A(-1, 0), B(1, 2) and C(2, 3) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of x - y + 1 = 0.
Graph of 3x + 2y - 12 = 0
3x + 2y - 12 = 0
⇒ 2y = (–3x + 12)
∴ y = (-3x + 12)/2 ...(ii)
Putting x = 0, we get y = 6.
Putting x = 2, we get y = 3.
Putting x = 4, we get y = 0.
Thus, we have the following table for the equation 3x + 2y - 12 = 0.
|
x |
0 |
2 |
4 |
|
y |
6 |
3 |
0 |
Now, plot the points P(0, 6) and Q(4, 0). The point B(2, 3) has already been plotted. Join PC and CQ to get the graph line PQ. Extend it on both ways.
Then, PQ is the graph of the equation 3x + 2y - 12 = 0.
The two graph lines intersect at C(2, 3).
∴ The solution of the given system of equations is x = 2 and y = 3.
Clearly, the vertices of ∆ACQ formed by these two lines and the x-axis are Q(4, 0), C(2, 3) and A(-1, 0).
Now, consider ∆ACQ.
Here, height = 3 units and base (AQ) = 5 units
∴ Area ∆ACQ = 1/2 × base × height sq. units
= 1/2 × 5 × 3
= 7.5 sq. units.
15. Solve graphically the system of equations
x – 2y + 2 = 0
2x + y – 6 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the x-axis.
Solution
From the first equation, write y in terms of x
y = (x + 2)/2 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -2, y = (-2 + 2)/2 = 0
For x = 2, y = (2 + 2)/2 = 2
For x = 4, y = (4 + 2)/2 = 3
Thus, the table for the first equation (x - 2y + 2 = 0) is
|
x |
-2 |
2 |
4 |
|
y |
0 |
2 |
3 |
Now, plot the points A(-2, 0), B(2, 2) and C(4, 3) on a graph paper and join A, B and C to get the graph of x - 2y + 2 = 0.
From the second equation, write y in terms of x
y = 6 – 2x ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 1, y = 6 – 2 = 4
For x = 3, y = 0
For x = 4, y = 6 – 8 = -2
So, the table for the second equation (2x + y - 6 = 0) is
|
x |
1 |
3 |
4 |
|
y |
4 |
0 |
-2 |
Now, plot the points D(1, 4), E(3, 0) and F(4, -2) on the same graph paper and join D, E and F to get the graph of 2x + y - 6 = 0.
From the graph, it is clear that, the given lines intersect at (2, 2).
So, the solution of the given system of equation is (2, 2).
From the graph, the vertices of the triangle formed by the given lines and the x-axis are (-2, 0), (2, 2) and (3, 0).
Now, draw a perpendicular from the intersection point B on the x-axis. So,
Area (∆BAE) = 1/2 × AE × BM
= 1/2 × 5 × 2
= 5 sq. units
Hence, the vertices of the triangle formed by the given lines and the x-axis are (-2, 0), (2, 2) and (3, 0) and the area of the triangle is 5 sq. units.
16. Solve graphically the system of equations
2x – 3y + 6 = 0
2x + 3y - 18 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Solution
From the first equation, write y in terms of x
y = (2x + 6)/3 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -3, y = (-6 + 6)/3 = 0
For x = 0, y = (0 + 6)/3 = 2
For x = 3, y = (6 + 6)/3 = 4
Thus, the table for the first equation (2x - 3y + 6 = 0) is
|
x |
-3 |
0 |
3 |
|
y |
0 |
2 |
4 |
Now, plot the points A(-3, 0), B(0, 2) and C(3, 4) on a graph paper and join A, B and C to get the graph of 2x - 3y + 6 = 0.
From the second equation, write y in terms of x
y = (18 – 2x)/3 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = (18 – 0)/3 = 6
For x = 3, y = (18 – 6)/3 = 4
For x = 9, y = (18 – 18)/3 = 0
So, the table for the second equation (2x + 3y - 18 = 0) is
|
x |
0 |
3 |
9 |
|
y |
6 |
4 |
0 |
Now, plot the points D(0, 6), E(3, 4) and F(9, 0) on the same graph paper and join D, E and F to get the graph of 2x + 3y - 18 = 0.
From the graph, it is clear that, the given lines intersect at (3, 4).
So, the solution of the given system of equation is (3, 4).
From the graph, the vertices of the triangle formed by the given lines and the y-axis are (0, 2), (0, 6) and (3, 4).
Now, draw a perpendicular from the intersection point E (or C) on the y-axis. So,
Area (∆EDB) = 1/2 × BD × EM
= 1/2 × 4 × 3
= 6 sq. units
Hence, the vertices of the triangle formed by the given lines and the y-axis are (0, 2), (0, 6) and (3, 4) and the area of the triangle is 6 sq. units.
17. Solve graphically the system of equations
4x – y – 4 = 0
3x + 2y - 14 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Solution
From the first equation, write y in terms of x
y = 4x – 4 ….(i)
Substitute different values of x in (i) to get different values of y
For x = 0, y = 0 – 4 = -4
For x = 1, y = 4 – 4 = 0
For x = 2, y = 8 – 4 = 4
Thus, the table for the first equation (4x - y – 4 = 0) is
|
x |
0 |
1 |
2 |
|
y |
-4 |
0 |
4 |
Now, plot the points A(0, -4), B(1, 0) and C(2, 4) on a graph paper and join A, B and C to get the graph of 4x – y – 4 = 0.
From the second equation, write y in terms of x
y = (14 – 3x)/2 ….(ii)
2y = 14 – 3x - 3x = 2y - 14
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = (14 – 0)/2 = 7
For x = 4, y = (14 – 12)/2 = 1
For x = 14/3, y = (14 – 14)/2 = 0
So, the table for the second equation (3x + 2y - 14 = 0) is
|
x |
0 |
4 |
14/3 |
|
y |
7 |
1 |
0 |
Now, plot the points D(0, 7), E(4, 1) and F(14/3, 0) on the same graph paper and join D, E and F to get the graph of 3x + 2y - 14 = 0.
From the graph, it is clear that, the given lines intersect at (2, 4).
So, the solution of the given system of equation is (2, 4).
From the graph, the vertices of the triangle formed by the given lines and the y-axis are (0, 7), (0, -4) and (2, 4).
Now, draw a perpendicular from the intersection point C on the y-axis. So,
Area (∆DAB) = 1/2 × DA × CM
= 1/2 × 11 × 2
= 11 sq. units
Hence, the vertices of the triangle formed by the given lines and the y-axis are (0, 7), (0, -4) and (2, 4) and the area of the triangle is 11 sq. units.
18. Solve graphically the system of equations
x – y – 5 = 0
3x + 5y - 15 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Solution
From the first equation, write y in terms of x
y = x – 5 ….(i)
Substitute different values of x in (i) to get different values of y
For x = 0, y = 0 – 5 = -5
For x = 2, y = 2 – 5 = -3
For x = 5, y = 5 – 5 = 0
Thus, the table for the first equation (x – y – 5 = 0) is
|
x |
0 |
2 |
5 |
|
y |
-5 |
-3 |
0 |
Now, plot the points A(0, -5), B(2, -3) and C(5, 0) on a graph paper and join A, B and C to get the graph of x – y – 5 = 0.
From the second equation, write y in terms of x
y = (15 – 3x)/5 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -5, y = (15 + 15)/5 = 6
For x = 0, y = (15 – 0)/5 = 3
For x = 5, y = (15 – 15)/5 = 0
So, the table for the second equation (3x + 5y - 15 = 0) is
|
x |
-5 |
0 |
5 |
|
y |
-6 |
3 |
0 |
Now, plot the points D(-5, 6), E(0, 3) and F(5, 0) on the same graph paper and join D, E and F to get the graph of 3x + 5y - 15 = 0.
From the graph, it is clear that, the given lines intersect at (5, 0).
So, the solution of the given system of equation is (5, 0).
From the graph, the vertices of the triangle formed by the given lines and the y-axis are (0, 3), (0, -5) and (5, 0).
Now, draw a perpendicular from the intersection point C on the y-axis. So,
Area (∆CEA) = 1/2 × EA × OC
= 1/2 × 8 × 5
= 20 sq. units
Hence, the vertices of the triangle formed by the given lines and the y-axis are (0, 3), (0, -5) and (5, 0) and the area of the triangle is 20 sq. units.
19. Solve graphically the system of equations
2x – 5y + 4 = 0
2x + y - 8 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Answer
From the first equation, write y in terms of x
y = (2x + 4)/5 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -2, y = (-4 + 4)/5 = 0
For x = 0, y = (0 + 4)/5 = 4/5
For x = 3, y = (6 + 4)/5 = 2
Thus, the table for the first equation (2x – 5y + 4 = 0) is
Now, plot the points A(-2, 0), B(0, 45) and C(3, 2) on a graph paper and join A, B and C to get the graph of 2x – 5y + 4 = 0.
From the second equation, write y in terms of x
y = 8 – 2x ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = 8 – 0 = 8
For x = 2, y = 8 – 4 = 3
For x = 4, y = 8 – 8 = 0
So, the table for the second equation (2x – 5y + 4 = 0) is
|
x |
0 |
2 |
4 |
|
y |
8 |
4 |
0 |
Now, plot the points D(0, 8), E(2, 4) and F(4, 0) on the same graph paper and join D, E and F to get the graph of 2x + y - 8 = 0.
From the graph, it is clear that, the given lines intersect at (3, 2).
So, the solution of the given system of equation is (3, 2).
The vertices of the triangle formed by the system of equations and y-axis are (0, 8), (0, 4/5) and (3, 2).
Draw a perpendicular from point C on the y-axis. So,
Area (∆DBC) = 1/2 × DB × CM
= 1/2 × (8 – 4/5) × 3
= 54/5 sq. units
Hence, the vertices of the triangle are (0, 8), (0, 4/5) and (3, 2) and its area is 54/5 sq. units.
20. Solve graphically the system of equations
5x - y = 7
x - y + 1 = 0.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 5x - y = 7
5x - y = 7
⇒ y = (5x – 7) …(i)
Putting x = 0, we get y = -7.
Putting x = 1, we get y = -2.
Putting x = 2, we get y = 3.
Thus, we have the following table for the equation 5x - y = 7.
| x | 0 | 1 | 2 |
| y | -7 | -2 | 3 |
Now, plot the points A(0, -7), B(1, -2) and C(2, 3) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of 5x - y = 7.
Graph of x - y + 1 = 0
x - y + 1 = 0
⇒ y = x + 1 ...(ii)
Putting x = 0, we get y = 1.
Putting x = 1, we get y = 2.
Putting x = 2, we get y = 3.
Thus, we have the following table for the equation x - y + 1 = 0.
| x | 0 | 1 | 2 |
| y | 1 | 2 | 3 |
Now, plot the points P(0, 1) and Q(1, 2). The point C(2, 3) has already been plotted. Join PQ and QC to get the graph line PC. Extend it on both ways.
Then, PC is the graph of the equation x - y + 1 = 0.
The two graph lines intersect at C(2, 3).
∴ The solution of the given system of equations is x = 2 and y = 3.
Clearly, the vertices of ∆APC formed by these two lines and the y-axis are P(0, 1), C(2, 3) and A(0, -7).
Now, consider ∆APC.
Here, height = 2 units and base (AP) = 8 units
∴ Area ∆APC = 1/2 × base × height sq. units
= 1/2 × 8 × 2
= 8 sq. units.
21. Solve graphically the system of equations
2x – 3y = 12
x + 3y = 6.
Find the coordinates of the vertices of the triangle formed by these two lines and the y-axis.
Solution
From the first equation, write y in terms of x
y = (2x – 12)/3 ….(i)
Substitute different values of x in (i) to get different values of y
For x = 0, y = (0 – 12)/3 = -4
For x = 3, y = (6 – 12)/3 = -2
For x = 6, y = (12 – 12)/3 = 0
Thus, the table for the first equation (2x – 3y = 12) is
| x | 0 | 3 | 6 |
| y | -4 | -2 | 0 |
Now, plot the points A(0, -4), B(3,-2) and C(6, 0) on a graph paper and join A, B and C to get the graph of 2x – 3y = 12.
From the second equation, write y in terms of x
y = (6 – x)/3 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = (6 – 0)/3 = 2
For x = 3, y = (6 – 3)/3 = 1
For x = 6, y = (6 – 6)/3 = 0
So, the table for the second equation (x + 3y = 6) is
| x | 0 | 3 | 6 |
| y | 2 | 1 | 0 |
Now, plot the points D(0, 2), E(3, 1) and F(6, 0) on the same graph paper and join D, E and F to get the graph of x + 3y = 6.
From the graph, it is clear that, the given lines intersect at (6, 0).
So, the solution of the given system of equation is (6, 0).
The vertices of the triangle formed by the system of equations and y-axis are (0, 2), (6, 0) and (0, -4).
Area (∆DAC) = 1/2 × DA × OC
= 1/2 × 6 × 6
= 18 sq. units
Hence, the vertices of the triangle are (0, 2), (6, 0) and (0, -4) and its area is 18 sq. units.
22. Show graphically that the system of equations 2x + 3y = 6, 4x + 6y = 12 has infinitely many solutions.
Solution
From the first equation, write y in terms of x
y = (6 – 2x)/3 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -3, y = (6 + 6)/3 = 4
For x = 3, y = (6 – 6)/3 = 0
For x = 6, y = (6 – 12)/3 = -2
Thus, the table for the first equation (2x + 3y = 6) is
| x | 0 | 3 | 6 |
| y | -4 | -2 | 0 |
Now, plot the points A(-3, 4), B(3, 0) and C(6, -2) on a graph paper and join A, B and C to get the graph of 2x + 3y = 6.
From the second equation, write y in terms of x
y = (12 – 4x)/6 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -6, y = (12 + 24)/6= 6
For x = 0, y = (12 – 0)/6 = 2
For x = 9, y = (12 – 36)/6 = -4
So, the table for the second equation (4x + 6y = 12) is
| x | -6 | 0 | 9 |
| y | 6 | 2 | -4 |
Now, plot the points D(-6, 6), E(0, 2) and F(9, -4) on the same graph paper and join D, E and F to get the graph of 4x + 6y = 12.
From the graph, it is clear that, the given lines coincidence with each other. Hence, the solution of the given system of equations has infinitely many solutions.
23. Show graphically that the system of equations 3x - y = 5, 6x - 2y = 10 has infinitely many solutions.
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' representing the x axis and y-axis, respectively.
Graph of 3x - y = 5
3x - y = 5
⇒ y = 3x - 5 …(i)
Putting x = 1, we get y = -2
Putting x = 0, we get y = -5
Putting x = 2, we get y = 1
Thus, we have the following table for the equation 3x - y = 5
| x | 1 | 0 | 2 |
| y | -2 | -5 | 1 |
Now, plot the points A(1, -2), B(0, -5) and C(2, 1) on the graph paper.
Join AB and AC to get the graph line BC. Extend it on both ways.
Thus, the line BC is the graph of 3x - y = 5.
Graph of 6x - 2y = 10
6x - 2y = 10
⇒ 2y = (6x – 10)
⇒ y = (6x - 10)/2 …(ii)
Putting x = 0, we get y = -5
Putting x = 1, we get y = -2
Putting x = 2, we get y = 1
Thus, we have the following table for the equation 6x - 2y = 10.
| x | 0 | 1 | 2 |
| y | -5 | -2 | 1 |
These are the same points as obtained for the graph line of equation (i).
It is clear from the graph that these two lines coincide.
Hence, the given system of equations has infinitely many solutions.
24. Show graphically that the system of equations 2x + y = 6, 6x + 3y = 18 has infinitely many solutions.
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' representing the x axis and y-axis, respectively.
Graph of 2x + y = 6
2x + y = 6
⇒ y = (6 – 2x) …(i)
Putting x = 3, we get y = 0
Putting x = 1, we get y = 4
Putting x = 2, we get y = 2
Thus, we have the following table for the equation 2x + y = 6
| x | 3 | 1 | 2 |
| y | 0 | 4 | 2 |
Now, plot the points A(3, 0), B(1, 4) and C(2, 2) on the graph paper.
Join AC and CB to get the graph line AB. Extend it on both ways.
Thus, the line AB is the graph of 2x + y = 6.
Graph of 6x + 3y = 18
6x + 3y = 18
⇒ 3y = (18 - 6x)
⇒ y = (18 – 6x)/3 ....(ii)
Putting x = 3, we get y = 0
Putting x = 1, we get y = 4
Putting x = 2, we get y = 2
Thus, we have the following table for the equation 6x + 3y = 18.
| x | 3 | 1 | 2 |
| y | 0 | 4 | 2 |
These are the same points as obtained for the graph line of equation (i).
Hence, the given system of equations has an infinite number of solutions.
25. Show graphically that the system of equations x - 2y = 5, 3x - 6y = 15 has infinitely many solutions.
Solution
From the first equation, write y in terms of x
y = (x – 5)/2 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -5, y = (-5 – 5)/2 = - 5
For x = 1, y = (1 – 5)/2 = - 2
For x = 3, y = (3 – 5)/2 = - 1
Thus, the table for the first equation (x - 2y = 5) is
|
x |
-5 |
1 |
3 |
|
y |
-5 |
-2 |
-1 |
Now, plot the points A(-5, -5), B(1, -2) and C(3, -1) on a graph paper and join A, B and C to get the graph of x - 2y = 5.
From the second equation, write y in terms of x
y = (3x – 15)/6 ....(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -3, y = (-9 – 15)/6 = - 4
For x = -1, y = (-3 – 15)/6 = - 3
For x = 5, y = (15 – 15)/6 = 0
So, the table for the second equation (3x - 6y = 15) is
|
x |
-3 |
-1 |
5 |
|
y |
-4 |
-3 |
0 |
Now, plot the points D(-3, -4), E(-1, -3) and F(5, 0) on the same graph paper and join D, E and F to get the graph of 3x - 6y = 15.
From the graph, it is clear that, the given lines coincide with each other.
Hence, the solution of the given system of equations has infinitely many solutions.
26. Show graphically that the system of equations x - 2y = 6, 3x - 6y = 0 is inconsistent.
Solution
From the first equation, write y in terms of x
y = (x – 6)/2 ….(i)
Substitute different values of x in (i) to get different values of y
For x = -2, y = (-2 – 6)/2 = - 4
For x = 0, y = (0 – 6)/2 = - 3
For x = 2, y = (2 – 6)/2 = -2
Thus, the table for the first equation (x - 2y = 5) is
|
x |
-2 |
0 |
2 |
|
y |
-4 |
-3 |
-2 |
Now, plot the points A(-2, -4), B(0, -3) and C(2, -2) on a graph paper and join A, B and C to get the graph of x - 2y = 6.
From the second equation, write y in terms of x
y = 1/2 x ...(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = -4, y = -4/2 = - 2
For x = 0, y = 0/2 = 0
For x = 4, y = 4/2 = 2
So, the table for the second equation (3x - 6y = 0) is
|
x |
-4 |
0 |
4 |
|
y |
-2 |
0 |
2 |
Now, plot the points D(-4, -2), O(0, 0) and E(4, 2) on the same graph paper and join D, E and F to get the graph of 3x - 6y = 0.
Hence, the system of equations has no solution and therefore is inconsistent.
27. Show graphically that the system of equations 2x + 3y = 4, 4x + 6y = 12 is inconsistent.
Solution
On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
Graph of 2x +3y = 4
2x + 3y = 4
⇒ 3y = (–2x + 4) .…(i)
Putting x = 2, we get y = 0
Putting x = -1, we get y = 2
Putting x = -4, we get y = 4
Thus, we have the following table for the equation 2x + 3y = 4.
|
x |
2 |
-1 |
-4 |
|
y |
0 |
2 |
4 |
Now, plot the points A(2, 0), B(-1, 2) and C(-4, 4) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, the line AC is the graph of 2x + 3y = 4.
Graph of 4x + 6y = 12
4x + 6y = 12
⇒ 6y = (-4x + 12)
⇒ y = (-4x + 12)/6 …(ii)
Putting x = 3, we get y = 0
Putting x = 0, we get y = 2
Putting x = 6, we get y = -2
Thus, we have the following table for the equation 4x + 6y = 12.
|
x |
3 |
0 |
6 |
|
y |
0 |
2 |
-2 |
Now, on the same graph, plot the points A(3, 0), B(0, 2) and C(6, -2).
Join PQ and PR to get the graph line QR. Extend it on both ways.
Thus, QR is the graph of the equation 4x + 6y = 12.
It is clear from the graph that these two lines are parallel and do not intersect when produced.
Hence, the given system of equations is inconsistent.
28. Show graphically that the system of equations 2x + y = 6, 6x + 3y = 20 is inconsistent.
Solution
From the first equation, write y in terms of x
y = 6 – 2x ….(i)
Substitute different values of x in (i) to get different values of y
For x = 0, y = 6 – 0 = 6
For x = 2, y = 6 – 4 = 2
For x = 4, y = 6 – 8 = -2
Thus, the table for the first equation (2x + y = 6) is
|
x |
0 |
2 |
4 |
|
y |
6 |
2 |
-2 |
Now, plot the points A(0, 6), B(2, 2) and C(4, -2) on a graph paper and join A, B and C to get the graph of 2x + y = 6.
From the second equation, write y in terms of x
y = (20 – 6x)/3 ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = (20 – 0)/3 = 20/3
For x = 10/3, y = (20 – 20)/3 = 0
For x = 5, y = (20 – 30)/3 = - 10/3
So, the table for the second equation (6x + 3y = 20) is
|
x |
0 |
10/3 |
5 |
|
y |
20/3 |
0 |
-10/3 |
Now, plot the points D(0, 20/3), O(10/3, 0) and E(5, -10/3) on the same graph paper and join D, E and F to get the graph of 6x + 3y = 20.
From the graph, it is clear that, the given lines do not intersect at all when produced. Hence, the system of equations has no solution and therefore is inconsistent.
29. Draw the graphs for the following equations on the same graph paper:
2x + y = 2
2x + y = 6
Find the co-ordinates of the vertices of the trapezium formed by these lines. Also, find the area of the trapezium so formed.
Solution
From the first equation, write y in terms of x
y = 2 – 2x ….(i)
Substitute different values of x in (i) to get different values of y
For x = 0, y = 2 – 0 = 2
For x = 1, y = 2 – 2 = 0
For x = 2, y = 2 – 4 = -2
Thus, the table for the first equation (2x + y = 2) is
|
x |
0 |
1 |
2 |
|
y |
2 |
0 |
-2 |
Now, plot the points A(0, 2), B(1, 0) and C(2, -2) on a graph paper and join A, B and C to get the graph of 2x + y = 2.
From the second equation, write y in terms of x
y = 6 – 2x ….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y = 6 – 0 = 6
For x = 1, y = 6 – 2 = 4
For x = 3, y = 6 – 6 = 0
So, the table for the second equation (2x + y = 6) is
| x | 0 | 1 | 3 |
| y | 6 | 4 | 0 |
Now, plot the points D(0, 6), E(1, 4) and F(3, 0) on the same graph paper and join D, E and F to get the graph of 2x + y = 6.
From the graph, it is clear that, the given lines do not intersect at all when produced. So, these lines are parallel to each other and therefore, the quadrilateral DABF is a trapezium. The vertices of the required trapezium are D(0, 6), A (0, 2), B(1, 0) and F(3, 0).
Now,
Area(Trapezium DABF) = Area (∆DOF) – Area(∆AOB)
= 1/2 × 3 × 6 – 1/2 × 1 × 2
= 9 – 1
= 8 sq. units
Hence, the area of the required trapezium is 8 sq. units.