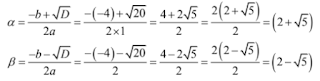RS Aggarwal Solutions Chapter 10 Quadratic Equation Exercise 10C Class 10 Maths
Chapter Name | RS Aggarwal Chapter 10 Quadratic Equation |
Book Name | RS Aggarwal Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 10C Solutions
1. Find the roots of the each of the following equations, if they exist, by applying the quadratic formula:
(i) 2x2 – 7x + 6 = 0
(ii) 3x2 – 2x + 8 = 0
(iii) 2x2 - 5√x + 4 = 0
(iv) √3x2 + 2√2x - 2√3 = 0
(v) (x – 1)(2x – 1) = 0
(vi) 1 – x = 2x2
Solution
(i) 2x2 – 7x + 6 = 0
Here,
a = 2,
b = - 7,
c = 6
Discriminant D is given by
D = b2 – 4ac
= (-7)2 – 4 × 2 × 6
= 49 – 48
= 1
(ii) 3x2 – 2x + 8 = 0
Here,
a = 3,
b = -2,
c = 8
Discriminant D is given by:
D = b2 – 4ac
= (-2)2 – 4 × 3 × 8
= 4 – 96
= - 92
(iii) 2x2 - 5√x + 4 = 0
Here,
a = 2,
b = -5√2,
c = 4
Discriminant D is given by:
D = b2 – 4ac
= (-5√2)2 – 4 × 2 × 4
= (25 × 2) – 32
= 50 – 32
= 18
(iv) √3x2 + 2√2x - 2√3 = 0
Here,
a = √3
b = 2√2,
c = -2√3
Discriminant D is given by:
D = b2 – 4ac
= (2√2)2 – 4 × √3 × (-2√3)
= (4 × 2) + (8 × 3)
= 8 + 24
= 32
(v) (x – 1)(2x – 1) = 0
⇒ 2x2 – 3x + 1 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 2, b = - 3 and c = 1
∴ Discriminant, D = b2 – 4ac
= (-3)2 – 4 × 2 × 1
= 9 – 8
= 1
(vi) 1 – x = 2x2
⇒ 2x2 + x – 1 = 0
Here,
a = 2,
b = 1,
c = - 1,
Discriminant D is given by:
D = b2 – 4ac
= 12 – 4 × 2(-1)
= 1 + 8
= 9
2. Find the roots of the each of the following equations, if they exist, by applying the quadratic formula:
(i) x2 – 4x – 1 = 0
Solution
x2 – 4x – 1 = 0
On comparing it with ax2 + bx + c = 0, we get:
a = 1, b = -4 and c =- 1
Discriminant D is given by:
D = (b2 – 4ac)
= (-4)2 – 4 × 1 × (-1)
= 16 + 4
= 20
= 20 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
(ii) x2 – 6x + 4 = 0
Solution
Given:
x2 – 6x + 4 = 0
On comparing it with ax2 + bx + c = 0, we get:
a = 1, b = - 6 and c = 4
Discriminant D is given by:
D = (b2 – 4ac)
= (-6)2 – 4 × 1 × 4
= 36 – 16
= 20 > 0
Hence, the roots of the equation are real.
Root α and β are given by:
Thus, the roots of the equation are (3 + 2√5) and (3 - 2√5).
(iii) 2x2 + x – 4 = 0
Solution
The given equation is 2x2 + x – 4 = 0.
Comparing it with ax2 + bx + c = 0, we get
a = 2, b = 1 and c = - 4
∴ Discriminant, D = b2 – 4ac = (1)2 - 4 × 2 × (-4)
= 1 + 32
= 33 > 0
So, the given equation has real roots.
Given:
25x2 + 30x + 7 = 0
On comparing it with ax2 + bx + x = 0, we get;
a = 25, b = 30 and c = 7
Discriminant D is given by:
D = (b2 – 4ac)
= (302 – 4 × 25 × 7)
= 900 – 700
= 200
= 200 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
Thus, the roots of the equation are (-3 + √2)/5 and (-3 – √2)/5.
(v) 16x2 + 24x + 1
Solution
16x2 + 24x + 1
⇒ 16x2 – 24x – 1 = 0
On comparing it with ax2 + bx + x = 0, we get;
a = 16, b = - 24 and c = - 1
Discriminant D is given by:
D = (b2 – 4ac)
= (24)2 – 4 × 16 × (-1)
= 576 + (64)
= 640 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
Solution
15x2 – 28 = x
⇒ 15x2 – x – 28 = 0
On comparing it with ax2 + bx + c = 0, we get:
a = 25, b = - 1 and c = - 28
Discriminant D is given by:
D = (b2 – 4ac)
= (1)2 – 4 × 15 × (-28)
= 1 – (-1680)
= 1 + 1680
= 1681
= 1681 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
Thus, the roots of the equation are 7/5 and (-4)/3.
(vii) 2x2 - 2√2x + 1 = 0
Solution
The given equation is 2x2 - 2√2x + 1 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 2, b = -2√2 and c = 1
∴ Discriminant, D = b2 – 4ac
= (-2√2)2 – 4 × 2 × 1
= 8 – 8
= 0
So, the given equation has real roots.
Now, √D = 0
∴ α = (-b + √D)/2a = -(-2√2)/(2 × 2) = (2√2)/4 = √2/2
β = (-b - √D)/2a = {-(-2√2) - √0}/(2 × 2) = 2√2/4 = √2/2
Hence, √2/2 is the repeated root of the given equation.
(viii) √2x2 + 7 + 5√2 = 0
Solution
The given equation is √2x2 + 7 + 5√2 = 0.
Comparing it with ax2 + bx + c = 0, we get
a = √2, b = 7 and c = 5√2
∴ Discriminant, D = b2 – 4ac
= (7)2 – 4 × √2 × 5√2 = 49 – 40
= 9 > 0
So, the given equation has real roots.
Now, √D = √9 = 3
∴ α = (-b + √D)/2a = (-7 + 3)/(2 × √2)
= -4/(2√2)
= -√2
β = (-b - √D)/2a
= (-7 – 3)/(2 × √2)
= -10/(2√2)
= -(5√2)/2
Hence, -√2 and –(5√2/2) are the root of the given equation.
(ix) √3x2 + 10x - 8√3 = 0
Solution
Given:
√3x2 + 10x - 8√3 = 0
On comparing it with ax2 + bx + x = 0, we get;
a = √3, b = 10 and c = -8√3
Discriminant D is given by:
D = (b2 – 4ac)
= (10)2 – 4 × √3 × (-8√3)
= 100 + 96
= 196 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
Thus, the roots of the equation are (2√3)/3 and –(4√3).
(x) √3x2 - 2√2x - 2√3 = 0.
Solution
The given equation is √3x2 - 2√2x - 2√3 = 0.
Comparing it with ax2 + bx + c = 0, we get
a = √3, b = -2√2 and c = -2√3
∴ Discriminant, D = b2 – 4ac
= (-2√2)2 – 4 × √3 × (-2√3)
= 8 + 24
= 32 > 0
So, the given equation has real roots.
Now, √D = √32 = 4√2
∴ α = (-b + √D)/2a = -(-2√2) + 4√2)/(2 × √3) = 6√2/2√3 = √6
β = (-b - √D)/2a = {-(-2√2) - 4√2)}/(2 × √3) = (-2√2)/(2√3) = -(√6/3)
Hence, √6 and –(√6/3) are the root of the given equation.
(xi) 2x2 + 6√3x – 60 = 0.
Solution
The given equation is 2x2 + 6√3x – 60 = 0.
Comparing it with ax2 + bx + c = 0, we get
a = 2, b = 6√3 and c = - 60
∴ Discriminant, D = b2 – 4ac
= (6√3)2 – 4 × 2 × (-60)
= 180 + 480
= 588 > 0
So, the given equation has real roots.
(xii) 4√3x2 + 5x - 2√3 = 0
Solution
The given equation is 4√3x2 + 5x - 2√3 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 4√3, b = 5 and c = -2√3
∴ Discriminant, D = b2 – 4ac
= 52 – 4 × 4√3 × (-2√3)
= 25 + 96
= 121 > 0
So, the given equation has real roots.
∴ α = (-b + √D)/2a = (-5 – 11)/(2 × 4√3) = 6/(8√3) = √3/4.
β = (-b - √D)/2a = (-5 – 11)/(2 × 4√3) = -16/(8√3)
= -(2√3)/3
Hence, √3/4 and –(2√3)/3 are the root of the given equation.
(xiii) 3x2 - 2√6x + 2 = 0
Solution
The given equation is 3x2 - 2√6x + 2 = 0
Comparing it with a2 + bx + c = 0, we get
a = 3, b = -2√6 and c = 2
∴ Discriminant, D = b2 – 4ac
= (-2√6)2 – 4 × 3 × 2
= 24 – 24
= 0
So, the given equation has real roots.
Now, √D = 0
∴ α = (- b + √D)/2a = -(-2√6) + 0/(2 × 3)
= (2√6)/6
= √6/3
β = (-b - √D)/2a = -(-2√6)/(2 × 3)
= (2√6)/6
= √6/3
Hence, √6/3 are the repeated of the given equation.
(xiv) 2√3x2 – 5x + √3 = 0
Solution
The given equation is 2√3x2 – 5x + √3 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 2√3, b = -5 and c = √3
∴ Discriminant, D = b2 – 4ac
= (-5)2 – 4 × 2√3 × √3
= 25 – 25
= 1 > 0
So, the given equation has real roots.
Now, √D = √1 = 1
∴ α = (-b + √D)/2a = -(-5 + 1) + 1/(2 × 2√3) = 6/(4√3) = √3/2
β = (-b - √D)/2a = -(-5) – 1/(2 × 2√3)
= 4/4√3
= √3/3
Hence, √3/2 and √3/3 are the roots of the given equation.
(xv) x2 + x + 2 = 0.
Solution
The given equation is x2 + x + 2 = 0
comparing it with ax2 + bx + c = 0, we get
a = 1, b = 1 and c = 2
∴ Discriminant D = b2 – 4ac = 12 – 4 × 1 × 2
= 1 – 8
= - 7 < 0
Hence, the given equation has no real roots (or real roots does not exist).
(xvi) 2x2 + ax – a2 = 0
Solution
The given equation is 2x2 + ax – a2 = 0
Comparing it with Ax2 + Bx + C = 0, we get
A = 2, B = a and C = - a2
∴ Discriminant, D = B2 – 4AC
= a2 – 4 × 2 × -a2
= a2 + 8a2
= 9a2 ≥ 0
So, the given equation has real roots.
Now, √D = √9a2 = 3a
∴ α = (-B + √D)/2A = (-a + 3a)/(2 × 2) = 2a/4 = a/2
β = (-B - √D)/2A = (-a – 3a)/(2 × 2) = -4a/4 = - a
Hence, a/2 and – a are the roots of the given equation.
(xvii) (x2 - √3 + 1)x + √3 = 0.
Solution
The given equation is x2 – (√3 + 1)x + √3 = 0.
Comparing it with ax2 + bx + c = 0, we get
a = 1, b = -(√3 + 1) and c = √3
∴ Discriminant,
D = b2 – 4ac = [-(√3 + 1)]2 – 4 × 1 × √3
= 3 + 1 + 2√3 - 4√3
= 3 - 2√3 + 1
= (√3 – 1)2 > 0
So, the given equation has real roots.
Solution
The given equation is 2x2 + 5√3x + 6 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 2, b = 5√3 and c = 6
∴ Discriminant, D = b2 – 4ac = (5√3)2 – 4 × 2 × 6
= 75 – 48
= 27 > 0
So, the given equation has real roots.
Now, √D = √27 = 3√3
∴ α = (-b + √D)/2A = (-5√3 + 3√3)/(2 × 2) = (-2√3)/4 = - √3/2
β = (-b - √D)/2a = (-5√3 – 3√3)/(2 × 2) = (-8√3)/4 = - 2√3
Hence, -√3/2 and -2√3 are the roots of the given equation.
(xix) 3x2 – 2x + 2 = 0.b
Solution
The given equation is 3x2 – 2x + 2 = 0
Comparing it with ax2 + bx + c = 0, we get
a = 3, b = - 2 and c = 2
∴ Discriminant D = b2 – 4ac
= (2)2 – 4 × 3 × 2
= 4 – 24
= - 20 < 0
Hence, the given equation has no real roots (or real roots does not exist).
(xx) x + 1/x = 3, x ≠ 0
Solution
The given equation is
x + 1/x = 3, x ≠ 0
⇒ (x2 + 1)/x = 3
⇒ (x2 + 1)/x = 3
⇒ x2 + 1 = 3x
⇒ x2 – 3x +1 = 0
This equation is of from of ax2 + bx + c = 0, where, a = 1, b = - 3 and c = 1.
∴ Discriminant, D = b2 – 4ac
= (-3)2 – 4 × 1 × 1
= 9 – 4
= 5 > 0
So, the given equation has real roots.
Now, √D = √5
∴ α = (-b + √D)/2a
= {-(-3) + √5)/(2 × 1) = (3 + √5)/2
β = (-b - √D)/2a = {-(-3) - √5)}/(2 × 1) = (3 - √5)/2
Hence, (3 + √5)/2 and (3 - √5)/2 are -the roots of the given equation.
(xxi) 1/x – 1/(x – 2) = 3, x ≠ 0, 2
Solution
The given equation is
1/x – 1/(x – 2) = 3, x ≠ 0, 2
⇒ (x – 2 – x)/(x(x – 2) = 3
⇒ -2/(x2 – 2x) = 3
⇒ - 2 = 3x2 – 6x
⇒ 3x2 – 6x + 2 = 0
This equation is of form ax2 + bx + c = 0, where = 3, b = -6, and c = 2.
∴ Discriminant, D = b2 – 4ac = (-6)2 - 4 × 3 × 2
= 36 – 24
= 12 > 0
So, the given equation has real roots.
Hence, (3 + √3)/3 and (3 - √3)/3 are the roots of the given equation.
(xxii) x – 1/x = 3, x ≠ 0
Solution
The given equation is
x – 1/x = 3, x ≠ 0
⇒ (x2 – 1)/x = 3
⇒ x2 – 1 = 3x
⇒ x2 – 3x – 1 = 0
This equation is of the form ax2 + bx + c = 0, where a = 1, b = - 3 and c = -1.
∴ Discriminant, D = b2 – 4ac
= (-3)2 – 4 × 1 × (-1)
= 9 + 4
= 13 > 0
So, the given equation has real roots.
Solution
The given equation is
m/nx2.n/m = 1 – 2x
⇒ (m2x2 + n2)/mn = 1 – 2x
⇒ m2x2 + n2 = mn – 2mnx
⇒ m2x2 + 2mnx + n2 – mn = 0
This equation is of the form ax2 + bx + c = 0, where a = m2, b = 2mn and c = n2 – mn
∴ Discriminant,
D = b2 – 4ac = (2mn)2 – 4 × m2 × (n2 – mn)
= 4m2n2 – 4m2n2 + 4m3n2
= 4m3n > 0
So, the given equation has real roots.
(xxiv) 36x2 – 12ax + (a2 – b2) = 0
Solution
The given equation is 36x2 – 12ax + (a2 – b2) = 0
Comparing it with Ax2 + Bx + C = 0, we get
A = 36, B = - 12a and C = a2 – b2
∴ Discriminant,
D = b2 – 4AC = (-12a)2 – 4 × 36 × (a2 – b2)
= 144a2 – 144a2 + 144b2
= 144b2
So, the given equation has real roots.
∴ α = (-B + √D)/2A
= {-(-12a) + 12b)/(2 × 36) = 12(a + b)/72 = (a + b)/0
β = (-B - √D)/2A = {-(-12a) – 12b)}/(2 × 36) = 12(a - b)/72
= (a – b)/6
Hence, (a + b)/6 and (a – b)/6 are the roots of the given equation.
(xxv) x2 – 2ax + (a2 – b2) = 0
Solution
x2 – 2ax + (a2 – b2) = 0
On comparing it with Ax2 + Bx + C = 0, we get;
A = 1, B = - 2a and C = (a2 – b2)
Discriminant D is given by:
D = b2 – 4AC
= (-2a)2 – 4 × 1 × (a2 – b2)
= 4a2 – 4a2 + 4b2
= 4b2 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
(xxvi) x2 – 2ax – (4b2 – a2) = 0
Solution
The given equation is x2 – 2ax – (4b2 – a2) = 0
Comparing it with Ax2 + Bx + C = 0, we get
A = 1, B = - 2a and C = -(4b2 – a2)
∴ Discriminant,
B2 – 4AC = (-2a)2 – 4 × 1 × [-(4b2 – a2)]
= 4a2 + 16b2 – 4a2
= 16b2 > 0
So, the given equation has real roots
∴ α = (-B + √D)/2A
= {-(-2a) + 4b)/(2 × 1) = 2(a + 2b)/2 = a + 2b
β = (-B - √D)/2A = {-(-2a) – 4b)}/(2 × 1) = 2(a - b)/2
= a – 2b
Hence, a + 2b and a – 2b are the roots of the given equation.
(xxvii) x2 + 6x – (a2 – 2a + 8) = 0.
Solution
The given equation is x2 + 6x – (a2 + 2a – 8) = 0
Comparing it with Ax2 + Bx + C = 0, we get
A = 1, B = 6 and C = - (a2 + 2a – 8)
∴ Discriminant,
D = B2 – 4AC = 62 – 4 × 1 × [-(a2 + 2a – 8)]
= 36 + 4a2 + 8a – 32
= 4a2 + 8a – 32
= 4a2 + 8a + 4
= 4(a2 + 2a + 1)
= 4(a + 1)2 > 0
So, the given equation has real roots
∴ α = (-B + √D)/2A
= (-6 + 2(a + 1))/(2 × 1) = (2a - 4)/2 = a - 2
β = (-B - √D)/2A = (- 6 – 2(a + 1))/(2 × 1) = (-2a – 8)/2
= - a – 4
= - (a + 4)
Hence, (a – 2) and – (a + 4) are the roots of the given equation.
(xxviii) x2 + 5x – (a2 – a - 6) = 0.
Solution
The given equation is x2 + 5x – (a2 + a – 6) = 0.
Comparing it with Ax2 + Bx + C = 0, we get
A = 1, B = 5 and C = - (a2 + a – 8)
∴ Discriminant,
D = B2 – 4AC
= 52 – 4 × 1 × [-(a2 + a – 6)]
= 25 + 4a2 + 4a - 24
= 4a2 + 4a2 + 4a + 1
= (2a + 1)2 > 0
So, the given equation has real roots
∴ α = (-B + √D)/2A
= (-5 + 2a + 1)/(2 × 1) = (2a - 4)/2 = a - 2
β = (-B - √D)/2A = (- 5 – 2(a + 1))/(2 × 1) = (-2a – 6)/2
= - a – 3
= - (a + 3)
Hence, (a – 2) and –(a + 3) are the roots of the given equation.
(xxix) x2 – 4ax – b2 + 4a2 = 0.
Solution
The given equation is x2 – 4ax – b2 + 4a2 = 0.
Comparing it with Ax2 + Bx + C = 0, we get
A = 1, B = - 4a and C = - b2 + 4a2
∴ Discriminant, D = B2 – 4AC
= (-4a)2 – 4 × 1 × (-b2 + 4a2)
= 16a2 + 4b2 – 16a2
= 4b2 > 0
So, the given equation has real roots
= (4a + 2b)/2 = 2a + b
β = (-B - √D)/2A = (-(-4a) – 2b)/(2 × 1) = (4a – 2b)/2
= 2a – b.
Hence, (2a + b) and (2a – b) are the roots of the given equation.
(xxx) 4x2 – 4a2x + (a4 – b4) = 0
Solution
The given equation is 4x2 – 4a2x + (a4 – b4) = 0.
Comparing it with Ax2 + Bx + C = 0, we get
A = 4, B = - 4a2 and C = a4 – b4
∴ Discriminant, B2 – 4AC
= (-4a2)2 – 4 × 4 × (a2 – b2)
= 16a4 – 16a4 + 16b4
= 16b4 > 0
So, the given equation has real roots
∴ α = (-B + √D)/2A = (-(-4a) + 4b2)/(2 × 4)
= 4(a2 + b2)/8
= (a2 + b2)/2
∴ β = (-B - √D)/2A
= -(-4a2) – 4b2/(2 × 4)
= 4(a2 – b2)/8
= (a2 – b2)/2
Hence, 1/2(a2 + b2) and 1/2(a2 – b2) are the roots of the given equation.
(xxxi) 4x2 – 4bx – (a2 – b2) = 0.
Solution
The given equation is 4x2 – 4bx – (a2 – b2) = 0
Comparing it with Ax2 + Bx + C = 0, we get
A = 4, B = 4b and C = -(a2 – b2)
∴ Discriminant,
D = B2 – 4AC
= (4b)2 – 4 × 4 × [-(a2 – b2)]
= 16b2 + 16a2 – 16b2
= 16a2 > 0
So, the given equation has real roots
∴ α = (-B + √D)/2A = (-4b + 4a)/(2 × 4)
= 4(a – b)/8 = (a – b)/2
∴ β = (-B - √D)/2A
= -4(a + b)/8
= -(a + b)/2
Hence, 1/2(a – b) and – 1/2(a + b) are the roots of the given equation.
(xxxii) 33. x2 – (2b – 1)x + (b2 – b – 20) = 0
Solution
The given equation is x2 – (2b – 1)x + (b2 – b – 20) = 0.
Comparing it with Ax2 + Bx + C = 0, we get
A = 1, B = -(2b – 1) and C = b2 – b – 20
∴ Discriminant,
D = B2 – 4AC
= [-(2b – 1)]2 – 4 × 1 × (b2 – b – 20)
= 4b2 – 4b + 1 – 4b2 + 4b + 80
= 81 > 0
So, the given equation has real roots
∴ α = (-B + √D)/2A = -[-(2b - 1) + 9]/(2 × 1)
= (2b + 8)/2
= b + 4
β = (-B - √D)/2A
= -[(-2b - 1)] - 9/(2 × 1)
= (2b – 10)/2
= b – 5
Hence, (b + 4) and (b – 5) are the roots of the given equation.
(xxxiii) 3a2x2 + 8abx + 4b2 = 0
Solution
3a2x2 + 8abx + 4b2 = 0
On comparing it with Ax2 + Bx + C = 0, we get:
A = 3a2, B = 8ab and C = 4b2
Discriminant D is given by:
D = (B2 – 4AC)
= (8ab)2 – 4 × 3a2 × 4b2
= 16a2b2 > 0
Hence, the roots of the equation are real.
Roots α and β are given by:
Thus, the roots of the equation are (-2b/3a) and (-2b/a).
(xxxiv) a2b2x2 – (4b4 – 3a4)x – 12a2b2 = 0, a ≠ 0 and b ≠ 0
Solution
The given equation is a2b2x2 – (4b4 – 3a4)x – 12a2b2 = 0
Comparing it with Ax2 + Bx + C = 0, we get
A = a2b2, B = -(4b4 – 3a4) and c = - 12a2b2
∴ Discriminant,
B2 – 4AC
= [-(4b4 – 3a4)]2 - 4 × a2b2 × (-12a2b2)
= 16b8 – 24a4b4 + 9a8 + 48a4b4
= 16b8 + 24a4b4 + 9a8
= (4b4 + 3a4)2 > 0
So, the given equation has real roots.
β = (- B - √D)/2A = [-[-(4b4 – 3a4)] – (4b4 + 3a4)]/(2 × a2b2)
= -6a4/2a2b2
= -(3a2/b2)
Hence, 4b2/a2 and – (3a2/b) are the roots of the given equation.
(xxxv) 12abx2 – (9a2 – 8b2)x – 6ab = 0, where a ≠ 0 and b ≠ 0
Solution
Given:
12abx2 – (9a2 – 8b2)x – 6ab = 0
On comparing it with Ax2 + Bx + C = 0, we get:
A = 12ab, B = -(9a2 – 8b2) and C = - 6ab
Discriminant D is given by:
D = B2 – 4AC
= [-(9a2 – 8b2)]2 – 4 × 12ab × (-6ab)
= 81a4 – 144a2b2 + 64b4 + 288a2b2
= 81a4 + 144a2b2 + 64b4
= (9a2 + 8b2)2 > 0
Hence, the roots of the equation are equal.
Roots α and β are given by:
Thus, the roots of the equation are 3a/4b and (-2b)/3a.