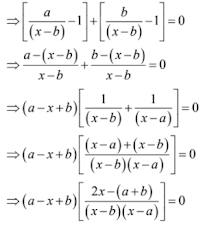RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equation Exercise 10A

RS Aggarwal Solutions Chapter 10 Quadratic Equation Exercise 10A Class 10 Maths

Chapter Name	RS Aggarwal Chapter 10 Quadratic Equation
Book Name	RS Aggarwal Mathematics for Class 10
Other Exercises	Exercise 10B Exercise 10C Exercise 10D Exercise 10E Exercise 10F
Related Study	NCERT Solutions for Class 10 Maths

Exercise 10A Solutions

1. Which of the following are quadratic equation in x ?

(i) x² – x + 2 = 0

(ii) 2x² + 5/2x – 3 = 0

(iii) √2x² + 7x + 5√2

(iv) 1/3x² + 1/5x – 2 = 0

(v) x² – 3x - √x + 4 = 0

(vi) x – 6/x = 3

(vii) x² – 2/x = x²

(viii) x² – 1/x² = 5

(ix) (x + 2)³ = x³ – 8

(x) (2x + 3(3x + 2) = 6(x – 1)(x – 2)

(xi) (x + 1/x)² = 2(x + 1/x) + 3

Solution

(i) (x² – x + 3) is a quadratic polynomial

∴ x² – x + 3 = 0 is a quadratic equation.

(ii) Clearly, (2x² + 5/2.x - √3) is a quadratic polynomial.

∴ 2x² + 5/2.x - √3 = 0 is a quadratic equation.

(iii) Clearly, (√2x² + 7x + 5√2) is a quadratic polynomial.

√2x² + 7x + 5√2 = 0 is a quadratic equation.

(iv) Clearly, (1/3x² + 1/5.x – 2) is a quadratic polynomial.

∴ 1/3x² + 1/5x – 2 = 0 is a quadratic equation.

(v) (x² – 3x - √x + 4) contains a term with √x, i.e., x^1/2, where 1/2 is not a integer.

Therefore, it is not a quadratic polynomial.

∴ x² – 3x - √x + 4 = 0 is not a quadratic equation.

(vi) x – 6/x = 3

⇒ x² – 6 = 3x

⇒ x² – 3x – 6 = 0

(x³ – 3x – 6) is not quadratic polynomial; therefore, the given equation is quadratic.

(vii) x² – 2/x = x²

⇒ x² + 2 = x³

⇒ x³ – x² – 2 = 0

(x³ – x² – 2) = 0 is not a quadratic polynomial.

∴ x³ – x² – 2 = 0 is not a quadratic equation.

(viii) x² – 1/x² = 5

⇒ x⁴ – 1 = 5x²

⇒ x⁴ – 5x² – 1 = 0

(x⁴ – 5x² - 1) is a polynomial with degree 4.

∴ x⁴ – 5x² – 1 = 0 is not a quadratic equation.

(ix) (x + 2)³ = x³ – 8

⇒ x³ + 6x² + 12x + 8 = x³ – 8

⇒ 6x² + 12x + 16 = 0

This is of form ax² + bx + c = 0

Hence, the given equation is a quadratic equation.

(x) (2x + 3)(3x + 2) = 6(x – 1)(x – 2)

⇒ 6x² + 4x + 9x + 6 = 6(x² – 3x + 2)

⇒ 6x² + 13x + 6 = 6x² – 18x + 12

⇒ 31x – 6 = 0

This is of the form ax² + bx + c = 0

Hence, the given equation is not a quadratic equation.

(xi) (x + 1/x)² = 2(x + 1/x) + 3

⇒ (x² + 1)/x)² = 2(x² + 1)/x + 3

⇒ (x² + 1)² = 2x(x² + 1) + 3x²

⇒ x⁴ + 2x² + 1 = 2x³ + 2x + 3x²

⇒ x⁴ – 2x³ – x² – 2x + 1 = 0

This is not of the form ax² + bx + c = 0

Hence, the given equation is not a quadratic equation.

2. Which of the following are the roots of 3x² + 2x – 1 = 0 = ?

(i) – 1

(ii) 1/3

(iii) – 1/2

Solution

The given equation is (3x² + 2x – 1 = 0).

(i) x = (-1)

LHS = x² + 2x – 1

= 3 × (-1)² + 2 × (-1) – 1

= 3 – 2 – 1

= 0

= R.H.S.

Thus, (-1) is a root of (3x² + 2x – 1 = 0).

(ii) On subtracting x = 1/3 in the given equation, we get:

L.H.S. = 3x² + 2x – 1

= 3 × (1/3)² + 2 × 1/3 – 1

= 3 × 1/9 + 2/3 – 1

= (1 + 2 – 3)/3

= 0/3

= 0

= R.H.S.

Thus, (1/3) is a root of (3x² + 2x – 1 = 0)

(iii) On subtracting x = (-1/2) in the given equation, we get

L.H.S = 3x² + 2x – 1

= 3 × (-1/2)² + 2 × (-1/2) – 1

= 3 × 1/4 – 1 – 1

= 3/4 – 2

= (3 – 8)/4

= -5/4 ≠ 0

Thus, L.H.S. = R.H.S.

Hence, (-1/2) is a solution of (3x² + 2x – 1 = 0).

3. Find the value of k for which x = 1 is a root of the equation x² + kx + 3 = 0.

Solution

It is given that (x = 1) is a root of (x² + kx + 3 = 0).

Therefore, (x = 1) must satisfy the equation.

⇒ (1)² + k × 1 + 3 = 0

⇒ k + 4 = 0

⇒ k = - 4

Hence, the required value of k is -4.

4. Find the value of a and b for which x = 3/4 and x = - 2 are the roots of the equation ax² + bx – 6 = 0

Solution

It is given that 3/4 is a root of ax³ + bx – 6 = 0; therefore, we have:

a × (3/4)² + b × 3/4 - 6 = 0

⇒ 9a/16 + 3b/4 = 6

⇒ (9a + 12b)/16 = 6

⇒ 9a + 12b – 96 = 0

⇒ 3a + 4b = 32 ....(i)

Again, (-2) is a root of ax² + bx – 6 = 0; therefore, we have:

a × (-2)² + b × (-2) – 6 = 0

⇒ 4a – 2b = 6

⇒ 2a – b = 3 ....(ii)

On multiplying (ii) by 4 and adding the result with (i), we get:

⇒ 3a + 4b + 8a – 4b = 32 + 12

⇒ 11a = 44

⇒ a = 4

Putting the value of a in (ii), we get:

2 × 4 – b = 3

⇒ 8 – b = 3

⇒ b = 5

Hence, the required values of a and b are 4 and 5, respectively.

5. (2x – 3)(3x + 1) = 0

Solution

(2x – 3)(3x + 1) = 0

⇒ 2x – 3 = 0 or 3x + 1 = 0

⇒ 2x = 3 or 3x = - 1

⇒ x = 3/2 or x = - 1/3

Hence, the roots of the given equation are 3/2 and -1/3.

6. 4x² + 5x = 0

Solution

4x² + 5x = 0

⇒ x(4x + 5) = 0

⇒ x = 0 or 4x + 5 = 0

⇒ x = 0 or x = - 5/4

Hence, roots of the given equations are 0 and -5/4.

7. 3x² – 243 = 0.

Solution

Given:

3x² – 243 = 0

⇒ 3(x² – 81) = 0

⇒ (x)² – (9)² = 0

⇒ (x + 9)(x – 9) = 0

⇒ x + 9 = 0 or x – 9 = 0

⇒ x = - 9 or x = 9

Hence, -9 and 9 are the roots of the equation 3x² – 243 = 0.

8. 2x² + x – 6 = 0

Solution

We write, x = 4x – 3 as 2x² × (-6)

= -12x²

= 4x × (-3x)

∴ 2x² + x – 6 = 0

⇒ 2x² + 4x – 3x – 6 = 0

⇒ 2x(x + 2) – 3(x + 2) = 0

⇒ (x + 2)(2x – 3) = 0

⇒ x + 2 = 0 or 2x – 3 = 0

⇒ x = - 2 or x = 3/2

Hence, the roots of the given equations are -2 and 3/2.

9. x² + 6x + 5 = 0

Solution

We write, 6x = x + 5x as x² × 5 = 5x² = x × 5x

∴ x² + 6x + 5 = 0

⇒ x² + x – 5x + 5 = 0

⇒ x(x + 1) + 5(x + 1) = 0

⇒ (x + 1)(x + 5) = 0

⇒ x + 1 = 0 or x + 5 = 0

⇒ x = - 1 or x = - 5

Hence, the roots of the given equations are -1 and -5.

10. 9x² – 3x – 2 = 0

Solution

We write, -3x = 3x – 6x as 9x² × (-2)

= -18x²

= 3x × (-6x)

∴ 9x² – 3x – 2 = 0

⇒ 9x² + 3x – 6x – 2 = 0

⇒ 3x(3x + 1) – 2(3x + 1) = 0

⇒ (3x + 1)(3x – 2) = 0

⇒ 3x + 1 = 0 or 3x – 2 = 0

⇒ x = -1/3 or x = 2/3

Hence, the roots of the given equations are -1/3 and 2/3.

11. x²+ 12x + 35 = 0

Solution

x² + 12 + 35 = 0

⇒ x² + 7x + 5x + 35 = 0

⇒ x(x + 7) + 5(x + 7) = 0

⇒ (x + 5)(x + 7) = 0

⇒ x + 5 = 0 or x + 7 = 0

⇒ x = - 5 or x = - 7

Hence, -5 and -7 are the roots of the equation x² + 12x + 35 = 0.

12. x² = 18x – 77

Solution

x² = 18x – 77

⇒ x² – 18x + 77 = 0

⇒ x² – (11x + 7x) + 77 = 0

⇒ x² – 11x – 7x + 77 = 0

⇒ x(x – 11) – 7(x – 11) = 0

⇒ (x – 7)(x – 11) = 0

⇒ x – 7 = 0 or x – 11 = 0

⇒ x = 7 or x = 11

Hence, 7 and 11 are the roots of the equations x² = 18x – 77.

13. 6x²+ 11x + 3 = 0.

Solution

Given:

6x² + 11x + 3 = 0

⇒ 6x² + 9x + 2x + 3 = 0

⇒ 3x(2x + 3) + 1(2x + 3) = 0

⇒ (3x + 1)(2x + 3) = 0

⇒ 3x + 1 = 0 or 2x + 3 = 0

⇒ x = -1/3 or x = -3/2

Hence, -1/3 and -3/2 are the roots of the equation 6x² + 11x + 3 = 0

14. 6x²+ x – 12 = 0.

Solution

Given:

6x² + x – 12 = 0

⇒ 6x² + 9x – 8x – 12 = 0

⇒ 3x(2x + 3) – 4(2x + 3) = 0

⇒ (3x – 4)(2x + 3) = 0

⇒ 3x – 4 = 0 or 2x + 3 = 0

⇒ x = 4/3 or x = -3/2

Hence, 4/3 and -3/2 are the roots of the equation 6x² + x – 12 = 0.

15. 3x² – 2x – 1 = 0

Solution

We write, -2x = -3x + x as 3x² × (-1) 

= -3x²

= (-3x) × x

∴ 3x² – 2x – 1 = 0

⇒ 3x(x – 1) + 1(x – 1) = 0

⇒ (x – 1)(3x + 1) = 0

⇒ x – 1 = 0 or 3x + 1 = 0

⇒ x = 1 or x = -1/3

Hence, the roots of the given equation are 1 and – 1/3.

16. 4x² – 9x = 100

Solution

Given:

4x² – 9x = 100

⇒ 4x² – 9x – 100 = 0

⇒ 4x² – (25x – 16x) – 100 = 0

⇒ 4x² – 25x + 16x – 100 = 0

⇒ x(4x – 25) + 4(4x – 25) = 0

⇒ (4x – 25)(x + 4) = 0

⇒ 4x – 25 = 0 x + 4 = 0

⇒ x = 25/4 or x = -4

Hence, the roots of the equation are 25/4 and -4.

17. 15x² – 28 = x

Solution

Given:

15x² – 28 = x

⇒ 15x² – x – 28 = 0

⇒ 15x² – (21x – 20x) – 28 = 0

⇒ 15x² – 21x + 20x – 28 = 0

⇒ 3x(5x – 7) + 4(5x – 7) = 0

⇒ (3x + 4)(5x – 7) = 0

⇒ 3x + 4 = 0 or 5x – 7 = 0

⇒ x = -4/3 or x = 7/5

Hence, the roots of the equation are -4/3 and 7/5.

18. 4 – 11x = 3x²

Solution

Given:

4 – 11x = 3x²

⇒ 3x² + 11x – 4 = 0

⇒ 3x² + 12x – x – 4 = 0

⇒ 3x(x + 4) - 1(x + 4) = 0

⇒ (x + 4)(3x – 1) = 0

⇒ x + 4 = 0 or 3x – 1 = 0

⇒ x = -4 or x = 1/3.

19. 48x² - 13x – 1 = 0

Solution

48x² – 13x – 1 = 0

⇒ 48x² – (16x – 3x) – 1 = 0

⇒ 48x² – 16x + 3x – 1 = 0

⇒ 16x(3x – 1) + 1(3x – 1) = 0

⇒ (16x + 1)(3x – 1) = 0

⇒ 16x + 1 = 0 or 3x – 1 = 0

⇒ x = -1/16 or x = 1/3

Hence, the roots of equation are -1/16 and 1/3.

20. x² + 2√2x – 6 = 0

Solution

2√2x = 3√2x - √2x as x² × (-6)

= - 6x²

= 3√2x × (-√2x)

∴ x² + 2√2x – 6 = 0

⇒ x² + 2√2x - √2x – 6 = 0

⇒ x(x + 3√2) - √2(x + 3√2) = 0

⇒ (x + 3√2)(x - √2) = 0

⇒ x + 3√2 = 0 or x - √2 = 0

⇒ x = -3√2 or x = √2

Hence, the roots of the given equation are -3√2 and √2

21. √3x² + 10x + 7√3 = 0

Solution

We write: 10x = 3x + 7x as √3x² × 7√3

= 21x³

= 3x × 7x

∴ √3x² + 10x + 7√3 = 0

⇒ √3x² + 3x + 7x + 7√3 = 0

⇒ √3x(x + √3) + 7(x + √3) = 0

⇒ (x + √3)(√3x + 7) = 0

⇒ x + √3 = 0 or √3x + 7 = 0

⇒ x = -√3 or x = -7/√3 = -(7√3)/3

Hence, the roots of the given equation are -√3 and (-7√3)/3.

22.√3x² + 11x + 6√3 = 0

Solution

√3x² + 11x + 6√3 = 0

⇒ √3x² + 9x + 2x + 6√3 = 0

⇒ √3x(x + 3√3) + 2(x + 3√3) = 0

⇒ (x + 3√3)(√3x + 2) = 0

⇒ x + 3√3 = 0 or √3x + 2 = 0

⇒ x = -3√3 or x = -2/√3

= (-2 × √3)/(√3 × √3)

= -2√3/3

Hence, the roots of the equation are -3√3 and (-2√3)/3.

23. 3√3 + 4x - √7 = 0

Solution

Given:

3√7x² + 4x - √7 = 0

⇒ 3√7x² + 7x – 3x - √7 = 0

⇒ √7x(3x + √7) – 1(3x + √7) = 0

⇒ (3x + √7)(√7 – 1) = 0

⇒ 3x + √7 = 0 or √7x – 1 = 0

⇒ x = -√7/3 or x = 1√7 = (1 × √7)/(√7 × √7)

= √7/7

Hence, the roots of the equations are -√7/3 and √7/7.

24. √7x² – 6x - 13√7 = 0

Solution

We write, -6x = 7x – 13 as √7x² × (-13√7)

= -91x²

= 7x × (-13x)

∴ √7x² + 7x – 13x - 13√7 = 0

⇒ √7x² + 7x – 13x - 13√7 = 0

⇒ √7x(x + √7) – 13(x + √7) = 0

⇒ (x + √7)(√7x – 13) = 0

⇒ x + √7 = 0 or √7x – 13 = 0

⇒ x = -√7 or x = 13/√7

= (13√7)/7

Hence, the roots of the given equation are - √7 and 13√7/7

25. 4√6x² – 13x - 2√6 = 0

Solution

4√6x² – 13x - 2√6 = 0

⇒ 4√6x² – 16x + 3x - 2√6 = 0

⇒ 4√2x (√3x - 2√2) + √3(√3x - 2√2) = 0

⇒ (4√2x + √3)(√3x - 2√2) = 0

⇒ 4√2x + √3 = 0 or √3x - 2√2 = 0

⇒ x = -√3/(4√2)

= (-√3 × √2)/(4√2 × √2)

= -√8/8

or x = 2√2/√3

= (2√2 × √3)/(√3 × √3)

= (2√6)/3

Hence, the roots of the equations are -√6/8 and 2√6/3.

26. 3x² - 2√6x + 2 = 0

Solution

We write, -2√6x

= -√6x and 3x² × 2

= 6x²

= (-√6x) × (-√6x)

∴ 3x² - 2√6x + 2 = 0

⇒ 3x² - √6x - √6x + 2 = 0

⇒ √3x(√3x - √2) - √2(√3x - √2) = 0

⇒ (√3x - √2)(√3x - √2) = 0

⇒ (√3x - √2)² = 0

⇒ √3x - √2 = 0

⇒ x = √2/√3 = √6/3

Hence, √6/3 vis the repeated root of the given equation.

27. √3x² - 2√2x - 2√3 = 0

Solution

We write, -2√2x

= -3√2x + √2x as √3x² × (-2√3)

= -6x²

= (-3√2x) × (√2x)

∴ √3x² - 2√2x - 2√3 = 0

⇒ √3x² - 3√2x + √2x - 2√3 = 0

⇒ √3x(x - √6) + √2(x - √6) = 0

⇒ (x - √6)( √3x + √2) = 0

⇒ x - √6 = 0 or √3x + √2 = 0

⇒ x - √6 = 0 or x = - √2/√3

= -√6/3

Hence, the roots of the given equation are √6 and -√6/3. 

28. x² - 3√5x + 10 = 0

Solution

We write, -3√5x

= -2√5x - √5x as x² × 10 = 10x²

= (-2√5x) × (-√5x)

∴ x² - 3√5x + 10 = 0

⇒ x² - 2√5x - √5x + 10 = 0

⇒ x(x - 2√5) - √5(x - 2√5) = 0

⇒ (x - 2√5)(x - √5) = 0

⇒ x(x - 2√5) - √5(x - 2√5) = 0

Hence, the roots of the given equations are √5 and 2√5.

29. x² – (√3 + 1)x + √3 = 0

Solution

x² – (√3x + 1)x + √3 = 0

⇒ x² - √3x – x + √3 = 0

⇒ x(x - √3) – 1(x - √3) = 0

⇒ (x - √3)(x – 1) = 0

⇒ x - √3 = 0 or x – 1 = 0

⇒ x = √3 or x = 1

Hence, 1 and √3 are the roots of the given equations.

30. x² + 3√3x – 30 = 0

Solution

We write, 3√3x = 5√3x - 2√3x as x² × (-30)

= -30x²

= 5√3x × (-2√3)x

∴ x² + 3√3x – 30 = 0

⇒ x² + 5√3x - 2√3x – 30 = 0

⇒ x(x + 5√3) - 2√3(x + 5√3) = 0

⇒ (x + 5√3)(x - 2√3) = 0

⇒ x + 5√3 = 0 or x - 2√3 = 0

⇒ x = -5/√3 or x = 2√3

Hence, the roots of the given equation are -5√3 and 2√3.

31. √2x² + 7x + 5√2 = 0

Solution

We write, 7x = 5x + 2x as √2x² × 5√2

= 10x²

= 5x × 2x

∴ √2x² + 7x + 5√2 = 0

⇒ √2x² + 5x + 2x + 5√2 = 0

⇒ x(√2x + 5) + √2(√2x + 5) = 0

⇒ (√2x + 5)(x + √2) = 0

⇒ x + √2 = 0 or √2x + 5 = 0

⇒ x = -√2 or x = -(5/√2) = -(5√2)/2

Hence, the roots of the given equation are -√2 and -(5√2)/2.

32. 5x² + 13x + 8 = 0

Solution

We write, 13x = 5x + 8x as 5x² × 8

= 40x²

= 5x × 8x

∴ 5x² + 13x + 8 = 0

⇒ 5x² + 5x + 8x + 8 = 0

⇒ 5x(x + 1) + 8(x +1) = 0

⇒ (x + 1)(5x + 8) = 0

⇒ x + 1 = 0 or 5x + 8 = 0

x = -1 or x = - (8/5)

Hence, -1 and -8/5 are the roots of the given equation.

33. x² – (1 + √2)x + √2 = 0

Solution

Given:

x² – (1 + √2)x + √2 = 0

⇒ x² – x - √2x + √2 = 0

⇒ x(x – 1) - √2(x – 1) = 0

⇒ (x - √2)(x – 1) = 0

 ⇒ x - √2 = 0 or x – 1 = 0

⇒ x = √2 or x = 1

Hence, the roots of the equation are √2 and 1.

34. 9x² + 6x + 1 = 0

Solution

9x² + 6x + 1 = 0

⇒ 9x² + 3x + 3x + 1 = 0

⇒ 3x(3x + 1) + 1(3x + 1) = 0

⇒ (3x + 1)(3x + 1) = 0

⇒ 3x + 1 = 0 or 3x + 1 = 0

⇒ x = -1/3 or x = -1/3

Hence, -1/3 is the root of the equation 9x² + 6x + 1 = 0.

35. 100x² – 20x + 1 = 0

Solution

We write, -20x = -10x – 10x as 100x² × 1

= 100x²

= (-10x) × (-10x)

∴ 100x² – 20x + 1 = 0

⇒ 100x² – 10x – 10x + 1 = 0

⇒ 10x(10x – 1) - 1(10x – 1) = 0

⇒ (10x – 1)(10x – 1) = 0

⇒ (10x – 1)² = 0

⇒ 10x – 1 = 0

⇒ x = 1/10

Hence, 1/10 is the repeated root of the given equation.

 

36. 2x² – x + 1/8 = 0

Solution

We write, -x = -x/2 – x/2 as 2x² × 1/8

= x²/4

= - (x/2) × - (x/2)

2x² – x + 1/8 = 0

⇒ 2x² – x/2 – x/2 + 1/8 = 0

⇒ 2x(x – 1/4) – 1/2(x – 1/4) = 0

⇒ (x – 1/4)(2x – 1/2) = 0

⇒ x – 1/4 = 0 or 2x – 1/2 = 0

⇒ x = 1/4 or x = 1/4

Hence, 1/4 is the repeated root of the given equation.

37. 10x – 1/x = 3

Solution

Given:

10x - 1/x = 3

⇒ 10x² – 1 = 3x  [Multiplying both sides by x]

⇒ 10x² – 3x – 1 = 0

⇒ 10x² – (5x – 2x) – 1 = 0

⇒ 10x² – 5x + 2x – 1 = 0

⇒ 5x(2x – 1) + 1(2x – 1) = 0

⇒ (2x – 1)(5x + 1) = 0

⇒ 2x – 1 = 0 or 5x + 1 = 0

⇒ x = 1/2 or x = -1/5

Hence, the roots of the equation are 1/2 and -1/5.

38. 2/x² - 5/x + 2 = 0

Solution

Given:

2/x² – 5/x + 2 = 0

⇒ 2 – 5x + 2x² = 0  [Multiplying both sides by x²]

⇒ 2x² – 5x + 2 = 0

⇒ 2x² – (4x + x) + 2 = 0

⇒ 2x² – 4x – x + 2 = 0

⇒ 2x(x – 2) – 1(x – 2) = 0

⇒ (2x – 1)(x – 2) = 0

⇒ 2x – 1 = 0 or x – 2 = 0

⇒ x = 1/2 or x = 2

Hence, the roots of the equation are 1/2 and 2.

39. 2x² + ax – a² = 0

Solution

We write, ax = 2ax – ax as 2x² × (- a²)

= -2a²x²

= 2ax × (- ax)

∴ 2x² + ax – a² = 0

⇒ 2x(x + a) – a(x + a) =- 0

⇒ (x + a)(2x – a) = 0

⇒ x + a = 0 or 2x – a = 0

⇒ x = -a or x = a/2

Hence, -a and a/2 are the roots of the given equation.

40. x²+ 4bx – (a² – b²) = 0

Solution

We write, 4bx = 2(a + b)x – 2(a – b)x as

4x² × [-(a² – b²)]

= -4(a² – b²)x²

= 2(a + b)x × [-2(a – b)x]

∴ 4x² + 4bx – (a² - b²) = 0

⇒ 4x² + 2(a + b)x – 2(a – b)x – (a – b)(a + b) = 0

⇒ 2x[2x + (a + b) – (a – b)[2x + (a + b)] = 0

⇒ [2x + (a + b)][2x – (a – b)] = 0

⇒ 2x + (a + b) = 0 or 2x – (a – b) = 0

⇒ x = -(a + b)/2 or x = (a – b)/2

Hence, -(a + b)/2 or x = (a – b)/2 are the roots of the given equation.

41. 4x² - 4a²x + (a⁴ – b⁴) = 0

Solution

We write, -4a²x = -2(a² + b²)x – 2(a² – b²)x as

4x² × (a⁴ – b⁴) = 4(a⁴ – b⁴)x²

= [-2(a² + b²)]x × [-2(a² – b²)]x

∴ 4x² – 4a²x + (a⁴ – b⁴) = 0

⇒ 4x² – 2(a² + b²)x – 2(a² – b²)x² = [-2(a² + b²)]x × [-2(a² – b²)]x

⇒ 2x[2x – (a² + b²)] – (a² – b²)[2x – (a² + b²)] = 0

⇒ [2x – (a² + b²)] [2x – (a² – b²)] = 0

⇒ 2x – (a² + b²) = 0 or 2x – (a² – b²) = 0

⇒ x = (a² + b²)/2 or (a² – b²)/2

Hence, (a² + b²)/2 and (a² – b²)/2 are the roots of the given equation.

42. x² + 5x – (a² + a – 6) = 0

Solution

We write, 5x = (a + 3)x – (a – 2)x as

x × [-(a² + a – 6)]

= -(a² + a – 6)x²

= (a + 3)x × [-(a – 2)x]

∴ x² + 5x – (a² + a – 6) = 0

⇒ x² + (a + 3)x – (a – 2)x –(a + 3)(a – 2) = 0

⇒ x[x + (a + 3)] – (a – 2)[x + (a + 3)] = 0

⇒ [x + (a + 3)][x – (a – 2)] = 0

⇒ x + (a + 3) = 0, x - (a – 2) = 0

⇒ x = -(a + 3) or x = a – 2

Hence, -(a + 3) and (a – 2) are the roots of the given equation.

43. x² – 2ax - (4b² – a²) = 0

Solution

We have, -2ax = (2b – a)x – (2b + a)x as

x² × [-(4b² – a²)]

= -(4b² – a²)x²

= (2b – a)x × [-(2b + a)x]

∴ x² – 2ax – (4b² – a²) = 0

⇒ x² + (2b – a)x – (2b + a)x – (2b – a)(2b + a) = 0

⇒ x[x + (2b – a)] – (2b + a)[x + (2b – a)] = 0

⇒ [x + (2b – a)][x – (2b + a)] = 0

⇒ x + (2b – a) = 0 or x – (2b + a) = 0

x = -(2b – a) or x = 2b + a

⇒ x = a – 2b or x = a + 2b

Hence, a – 2b and a + 2b are the roots of the given equation.

44. x² – (2b – 1)x + (b² – b – 20) = 0

Solution

We write, -(2b – 1)x = -(b – 5)x – (b + 4)x as

x² × (b² – b – 20) = (b² – b – 20)x²

= [-(b – 5)x] × [-(b + 4)x]

∴ x² – (2b – 1)x + (b² – b – 20) = 0

⇒ x² – (b – 5)x – (b + 4)x + (b – 5)(b + 4) = 0

⇒ x[x – (b – 5)] – (b + 4)[x – (b – 5)] = 0

⇒ [x – b – 5]9x + (b + 4)] = 0

⇒ x – (b – 5) = 0 or x – (b + 4) = 0

⇒ x = b – 5 or x = b + 4

Hence, b – 5 and b + 4 are the roots of the given equation.

45. x² + 6x - (a² + 2a – 8) = 0

Solution

We write, 6x = (a + 4)x – (a – 2)x as

x² × [-(a² + 2a – 8)] = -(a² + 2a – 8)x²

= (a + 4)x × [-(a – 2)x]

∴ x² + 6x – (a² + 2a – 8) = 0

⇒ x² + (a + 4)x – (a – 2)x – (a + 4)(a – 2) = 0

⇒ x[x + (a + 4)] – (a – 2)[x + (a = 4)] = 0

⇒ [x + (a + 4)][x – (a – 2)] = 0

⇒ x + (a + 4) = 0 or x – (a – 2) = 0

⇒ x = - (a + 4) = 0 x = a – 2

Hence, -(a + 4) and (a – 2) are the roots of the given equation.

46. abx² + (b² – ac)x – bc = 0

Solution

abx² + (b² – ac)x – bc = 0

⇒ abx² + b²x – acx – bc = 0

⇒ bx(ax + b) – c(ax + b) = 0

⇒ (bx – c) (ax + b) = 0

⇒ bx – c = 0 or ax + b = 0

⇒ x = c/b or x = -b/a

Hence, the roots of the equation are c/b and -b/a.

47. x² – 4ax – b² + 4a² = 0

Solution

We write, -4ax = -(b + 2a)x + (b – 2a)x as

x² × (-b² + 4a²) = (-b² + 4a²)x²

= -(b + 2a)x × (b – 2a)x

∴ x² – 4ax – b² + 4a² = 0

⇒ x² – (b + 2a)x(b – 2a)x – (b – 2a)(b + 2a) = 0

⇒ x[x – (b + 2a)] + (b – 2a)[x – (b + 2a)] = 0

⇒ [x – (b + 2a)][x + (b – 2a)] = 0

⇒ x – (b + 2a) = 0 or x + (b – 2a) = 0

⇒ x = 2a + b or x = -(b – 2a)

⇒ x = 2a + b or x = 2a – b

Hence, (2a + b) and (2a – b) are the roots of the given equation.

48. 4x² – 2(a² + b²)x + a²b² = 0

Solution

4x² – 2(a² + b²)x + a²b² = 0

⇒ 4x² – 2a²x – 2b²x + a²b² = 0

⇒ 2x(2x – a²) – b²(2x – a²) = 0

⇒ (2x – b²)(2x – a²) = 0

⇒ 2x – b² = 0 or 2x – a² = 0

⇒ x = b²/2 or x = a²/a

Hence, the roots of equation are b²/2 and a²/2.

49. 12abx²– (9a² – 8b²)x – 6ab = 0

Solution

Given:

12abx² – (9a² – 8b²)x – 6ab = 0

⇒ 12abx² – 9a²x + 8b²x – 6ab = 0

⇒ 3ax(4bx – 3a) + 2b(4bx – 3a) = 0

⇒ (3ax + 2b)(4bx - 3a) = 0

⇒ 3ax + 2b = 0 or 4bx – 3a = 0

⇒ x = -2b/3a or x = 3a/4b

Hence, the roots of the equation are -2b/3a and 3a/4b.

50. a²b²x²+ b²x – a²x – 1 = 0.

Solution

Given:

a²b²x + b²x – a²x – 1 = 0

⇒ b²x(a²x + 1) – 1(a²x + 1) = 0

⇒ (b²x – 1)(a²x + 1) = 0

⇒ (b²x – 1) = 0 or (a²x + 1) = 0

⇒ x = 1/b² and -1/a² are the roots of the given equation.

51. 9x²– 9(a + b)x + (2a²+ 5ab + 2b²) = 0

Solution

We write, -9(a + b)x = -3(2a + b)x – 3(a + 2b)x as

9x² × (2a² + 5ab + 2b²)

= 9(2a² + 5ab + 2b2)x²

= [-3(2a + b)x] × [-3(a + 2b)x]

∴ 9x² – 9(a + b)x + (2a² + 5ab + 2b²) = 0

⇒ 9x² – 3(2a + b)x – 3(a + 2b)x + (2a + b)(a + 2b) = 0

⇒ 3x[3x – (2a + b)] – (a + 2b)[3x – (2a + b)] = 0

⇒ [3x – (2a + b)][3x – (a + 2b)] = 0

⇒ 3x – (2a + b) = 0 or 3x – (a + 2b) = 0

⇒ x = (2a + b)/3 or x = (a + 2b)/3

Hence, (2a + b)/3 and (a + 2b)/3 are the roots of the given equation.

52. 16/x – 1 = 15/(x + 1), x ≠ 0 , -1

Solution

16/x – 1 = 15/(x + 1), x 4≠ 0, 1

⇒ 16/x – 1 = 15/(x + 1) = 1

⇒ (16x + 16 – 15x)/x(x + 1) = 1

⇒ (x + 16)/(x² + x) = 1

⇒ x² + x = x + 16 (Cross multiplication)

⇒ x² – 16 = 0

⇒ (x + 4)(x – 4) = 0

⇒ x + 4 = 0 or x – 4 =0

⇒ x = -4 or x = 4

Hence, -4 and 4 are the roots of the given equation.

53. 4/x – 3 = 5/(2x + 3), x ≠ 0, -(3/2)

Solution

4/x – 3 = 5/(2x + 3), x ≠ 0, -(3/2)

⇒ 4/x – 5/(2x + 3) = 3

⇒ (8x + 12 – 5x)/x(2x + 3) = 3

⇒ (3x + 12)/(2x² + 3x) = 3

⇒ (x + 4)/(2x² + 3x) = 1

⇒ 2x² + 3x = x + 4 (Cross multiplication)

⇒ 2x² + 2x – 4 = 0

⇒ x² + x – 2 = 0

⇒ x² + 2x – x – 2 = 0

⇒ x(x + 2) – 1(x + 2) = 0

⇒ (x + 2)(x – 1) = 0

⇒ x + 2 = 0 or x – 1 = 0

⇒ x = -2 or x = 1

Hence, -2 and 1 are the roots of the given equation.

54. 3/(x + 1) - 1/2 = 2/(3x - 1), x = -1, 1/3 

Solution 

3/(x + 1) - 1/2 = 2/(3x - 1), x ≠ -1, 1/3

⇒ 3/(x + 1) – 2/(3x – 1) = 1/2

⇒ (9x – 3 – 2x – 2)/(x + 1)(3x – 1) = ½

⇒ (7x – 5)/(3x² + 2x – 1) = 1/2

⇒ 3x² + 2x – 1 = 14x – 10 (Cross multiplication)

⇒ 3x² – 12x + 9 = 0

⇒ x² – 4x + 3 = 0

⇒ x² – 3x – x + 3 = 0

⇒ x(x – 3) – 1(x – 3) = 0

⇒ (x – 3)(x – 1) = 0

⇒ x – 3 = 0 or x – 1 = 0

⇒ x = 3 or x = 1

Hence, 1 and 3 are the roots of the given equation.

55. 1/(x – 1) – 1/(x + 5) = 6/7, x ≠ 1, -5

Solution

1/(x – 1) – 1/(x + 5) = 6/7, x ≠ 1, -5

⇒ (x + 5 – x + 1)/(x – 1)(x + 5) = 6/7

⇒ 6/(x² + 4x – 5) = 6/7

⇒ x² + 4x – 5 = 7

⇒ x² + 4x – 12 = 0

⇒ x² + 6x – 2x – 12 = 0

⇒ x(x + 6) – 2(x + 6) = 0

⇒ (x + 6)(x – 2) = 0

⇒ x + 6 = 0 or x – 2 = 0

⇒ x = -6 or x = 2

Hence, -6 and 2 are the roots of the given equation.

56. 1/(2a + b + 2x) = 1/2a + 1/b + 1/2x

Solution

1/(2a + b + 2x) = 1/2a + 1/b + 1/2x

⇒ 1/2a + b + 2x) – 1/2x = 1/2a + 1/b

⇒ (2x – 2a – b – 2x)/(2x(2a + b + 2x) = (2a + b)/2ab

⇒ -(2a + b)/(4x² + 4ax + 2bx) = (2a + b)/2ab

⇒ 4x² + 4ax + 2bx = -2ab

⇒ 4x² + 4ax + 2bx = -2ab

⇒ 4x² + 4ax + 2bx + 2ab = 0

⇒ 4x(x + a) + 2b(x + a) = 0

(x + a)(4x + 2b) = 0

⇒ x + a(4x + 2b) = 0

⇒ x + a = 0 or 4x + 2b = 0

⇒ x = -a or x = -(b/2)

Hence, -a and -(b/2) are the roots of the given equation.

57. (x + 3)/(x – 2) - (1 – x)/x = 4.1/4 , x ≠ 2, 0

Solution

Given:

(x + 3)/(x – 2) – (1 – x)/x = 17/4

 ⇒ [x(x + 3) – (1 – x)(x – 2)]/[(x – 2)x] = 17/4

⇒ [x² + 3x – (x – 2 – x² + 2x)]/(x² – 2x) = 17/4

⇒ (x² + 3x + x² – 3x + 2)/(x² – 2x) = 17/4

⇒ (2x² + 2)/(x² – 2x) = 17/4

⇒ 8x² + 8 = 17x² – 34x

⇒ -9x² + 34x – 8 = 0

⇒ 9x² – 34x – 8 = 0

⇒ 9x² – 36x +2x – 8 = 0

⇒ 9x(x – 4) + 2(x – 4) = 0

⇒ (x – 4)(9x + 2) = 0

⇒ x – 4 = 0 or 9x + 2 = 0 ≠

⇒ x = 4 or x = -2/9

Hence, the roots of the equation are 4 and -2/9.

58. (3x – 4)/7 + 7/(3x – 4) = 5/2, x ≠ 4/3

Solution

(3x – 4)/7 + 7/(3x – 4) = 5/2, x ≠ 4/3

⇒ (3x – 4)2 + 49/7(3x – 4) = 5/2

 ⇒ 9x² – 24x + 16 + 49)/(21x – 28) = 5/2

⇒ 18x² – 48x + 130 = 105x – 140

 ⇒ 18x² – 153x + 270 = 0

⇒ 2x² – 17x + 30 = 0

⇒ 2x² – 12x – 5x + 30 = 0

⇒ 2x(x – 6) – 5(x – 6) = 0

⇒ (x – 6)(2x – 5) = 0

⇒ x – 6 = 0 or 2x – 5 = 0

⇒ x = 6 or x = 5/2

Hence, 6 and 5/2 are the roots of the given equation.

59. x/(x – 1) + (x – 1)/x = 4.1/4, x ≠ 0, 1

Solution

x/(x – 1) + (x – 1)/x = 4.1/4, x ≠ 0, 1

⇒ x²  + (x – 1)²/(x(x – 1)) = 17/4

⇒ (x² + x² – 2x + 1)/(x³ – x) = 17/4

⇒ (2x² – 2x + 1)/(x² – 1) = 17/4

⇒ 8x² – 8x + 4 = 17x² – 17x

⇒ 9x² – 9x – 4 = 0

⇒ 9x² – 12x + 3x – 4 = 0

⇒ 3x(3x – 4) + 1(3x – 4) = 0

⇒ (3x – 4)(3x + 1) = 0

⇒ (3x – 4)(3x + 1) = 0

⇒ 3x – 4 = 0 or 3x + 1 = 0

⇒ x = 4/3 or x = -(1/3)

Hence, 4/3 and -1/3 are the roots of the given equation.

60. x/(x + 1) + (x + 1)/x = 2.4/15, x ≠ 0, -1

Solution

x/(x +1) + (x + 1)/x = 2.4/15, x ≠ 0, -1

⇒ x² + (x + 1)2/x(x + 1) = 34/15

⇒ (x² + x² + 2x + 1)/(x² + x) = 34/15

⇒ (2x² + 2x + 1)/(x² + 1) = 34/15

⇒ 30x² + 30x + 15 = 34x² + 34x

⇒ 4x² + 4x – 15 = 0

⇒ 4x² + 10x – 6x – 15x = 0

⇒ 2x(2x + 5) – 3(2x + 5) = 0

⇒ (2x + 5)(2x – 3) = 0

⇒ 2x + 5 = 0 or 2x – 3 = 0

⇒ x = -5/2 or 2x – 3 = 0

Hence, -5/2 and 3/2 are the roots of the given equation.

61. (x – 4)/(x – 5) + (x – 6)/(x – 7) = 3.1/3, x ≠ 5, 7

Solution

(x – 4)/(x – 5) + (x – 6)/(x – 7) = 3.1/3, x ≠5, 7

⇒ (x – 4)(x – 7) + (x – 5)(x – 6)/{(x – 5)(x – 7)} = 10/3

⇒ (x² – 11x + 28 + x² – 11x + 30)/(x² – 12x + 35) = 10/3

⇒ (2x² – 22x + 58)/(x² – 12x + 35) = 10/3

⇒ (x² – 11x + 29)/(x² – 12x + 35) = 5/3

⇒ 3x² – 33x + 87 = 5x² – 60x + 175

⇒ 2x² – 33x + 87 = 5x² – 60x + 175

⇒ 2x² – 27x + 88 = 0

⇒ 2x² – 16x – 11x + 88 = 0

⇒ 2x(x – 8) – 11(x – 8) = 0

⇒ (x – 8)(2x – 11) = 0

⇒ x – 8 = 0 or 2x – 11 = 0

⇒ x = 8 or x = 11/2

Hence, 8 and 11/2 are the roots of the given equation.

62. (x – 1)/(x – 2) + (x – 3)/(x – 4) = 3.1/3, x ≠ 2, 4

Solution

(x – 1)/(x – 2) + (x – 3)/(x – 4) = 3.1/3, x ≠ 2, 4

⇒ (x – 1)(x – 4) + (x – 2)(x – 3)}/{(x – 2)(x – 4) = 10/3

⇒ (x² – 5x + 4 + x² – 5x + 6)/(x² – 6x + 8) = 10/3

 ⇒ (2x² – 10x + 10)/(x² – 6x + 8) = 10/3

⇒ (x² – 5x + 5)/(x² – 6x + 8) = 5/3

⇒ 3x² – 15x + 15 = 5x² – 30x + 40

⇒ 2x² – 15x + 25 = 0

⇒ 2x² – 10x – 5x + 25 = 0

⇒ 2x(x – 5) – 5(x – 5) = 0

⇒ (x – 5)(2x – 5) = 0

⇒ x – 5 = 0 or 2x – 5 = 0

⇒ x = 5 or x = 5/2

Hence, 5 and 5/2 are the roots of the given equation.

63. 1/(x – 2) + 2/(x – 1) = 6/x, x ≠ 0, 1, 2

Solution

1/(x – 2) + 2/(x – 1) = 6/x

⇒ (x – 1) + 2(x – 2)/(x – 1)(x – 2) = 6/x

⇒ (3x – 5)/(x2 – 3x + 2) = 6/x

⇒ 3x² – 5x = 6x² – 18x + 12 [On cross multiplying]

⇒ 3x² – 13x + 12 = 0

⇒ 3x² – (9 + 4)x + 12 = 0

⇒ 3x² – 9x – 4x + 12 = 0

⇒ 3x(x – 3) – 4(x – 3) = 0

⇒ (3x – 4)(x – 3) = 0

⇒ 3x – 4 = 0 or x – 3 = 0

⇒ x = 4/3 or x = 3

64. 1/(x + 1) + 2/(x + 2) = 5/(x + 4), x ≠ -1, -2, -4

Solution

1/(x + 1) + 2/(x + 2) = 5/(x + 4), x ≠ -1, -2, -4

⇒ (x + 2 + 2x + 2)/(x + 1)(x + 2) = 5/(x + 4)

⇒ (3x + 4)/(x² + 3x + 2) = 5/(x + 4)

⇒ (3x + 4)(x + 4) = 5(x² + 3x + 2)

⇒ 3x² + 16x + 16 = 5x² + 15x + 10

⇒ 2x² – x – 6 = 0

⇒ 2x² – 4x + 3x – 6 = 0

⇒ 2x(x – 2) + 3(x – 2) = 0

⇒ (x – 2)(2x + 3) = 0

⇒ 3x² + 16x + 16 = 5x² + 15x + 10

⇒ 2x² – x – 6 = 0

⇒ 2x² – 4x + 3x – 6 = 0

⇒ 2x(x – 2) + 3(x – 2) = 0

⇒ (x – 2)(2x + 3) = 0

⇒ x – 2 = 0 or 2x + 3 = 0

⇒ x = 2 or x = -3/2

Hence, 2 and -3/2 are the roots of the given equation.

65. 3(3x – 1)/(2x + 3) – 2(2x + 3)/(3x – 1) = 5, x ≠ 1/3, -3/2

Solution

3(3x – 1)/(2x + 3) – 2(2x + 3)/(3x – 1) = 5, x ≠ 1/3, -3/2

⇒ 3(3x – 1)² – 2(2x + 3)²/(2x + 3)(3x – 1) = 5

⇒ 3(9x² – 6x + 1) – 2(4x² + 12x + 9)/(6x² + 7x – 3) = 5

⇒ (27x² – 18x + 3 – 8x² – 24x – 18)/(6x² + 7x – 3) = 5

⇒ (19x² – 42x – 15)/(6x² + 7x – 3) = 5

⇒ 19x² – 42x – 15 = 30x2 + 35x – 15

⇒ 11x² + 77x = 0

⇒ 11x(x + 7) = 0

⇒ x = 0 or x + 7 = 0

⇒ x = 0 or x = - 7

Hence, 0 and -7 are the roots of the given equation.

66. 3(7x + 1)/(5x – 3) – 4(5x – 3)/(7x + 1) = 11, x ≠ 3/5, - 1/7

Solution

3(7x + 1)/(5x – 3) – 4(5x – 3)/(7x + 1) = 11, x ≠ 3/5, - 1/7

⇒ {3(7x + 1)² – 4(5x – 3)²}/(5x – 3)(7x + 1) = 11

⇒ 3(49x² +1 4x + 1) – 4(25x³ – 30x + 9)/(35x² – 16x – 3) = 11

⇒ (147x² + 42x + 3 – 100x² + 120x – 36)/(35x² – 16x – 3) = 11

⇒ (47x² + 162x – 33)/(35x² – 16x – 3) = 11

⇒ 338x(x – 1) = 0

⇒ x = 0 or x – 1 = 0

⇒ x = 0 x – 1 = 0

⇒ x = 0 or x = 1

Hence, 0 and 1 are the roots of the given equation.

67. (4x – 3)/(2x + 1) – 10(2x + 1)/(4x – 3) = 3, x ≠ -1/2, 3/4

Solution

Given:

(4x – 3)/(2x – 1) – 10(2x + 1)/(4x – 3) = 3

Putting (4x – 3)/(2x + 1) = y, we get:

y - 10/y = 3

⇒ (y² – 10)/y = 3

⇒ y² – 10 = 3y [On cross multiplying]

⇒ y² – 3y – 10 = 0

⇒ y² – (5 – 2)y – 10 = 0

⇒ y² – 5y + 2y – 10 = 0

⇒ y(y – 5) + 2(y – 5) = 0

⇒ (y – 5)(y + 2) = 0

⇒ y – 5 = 0 or y + 2 = 0

⇒ y = 5 or y = -2

Case I:

If y = 5, we get:

⇒ (4x – 3)/(2x + 1) = 5

⇒ 4x – 3 = 5(2x + 1) [On cross multiplying]

⇒ 4x – 3 = 10x + 5

⇒ -6x = 8

⇒ -6x = 8

⇒ x = 8/6

⇒ x = -(4/3)

Case II:

If y = -2, we get:

(4x – 3)/(2x + 1) = -2

⇒ 4x – 3 = -2(2x + 1)

⇒ 4x – 3 = -4x – 2

⇒ 8x = 1

⇒ x = 1/8

Hence, the roots of the equation are –(4/3) and 1/8.

68. (x/(x + 1))² – 5(x/(x + 1)) + 6 = 0, x ≠ b, a

Solution

(x/(x + 1))² – 5(x/(x + 1)) + 6 = 0

Putting x/(x + 1) = y, we get:

y² – 5y + 6 = 0

⇒ y² – 5y + 6 = 0

⇒ y² – (3 + 2) y + 6 = 0

⇒ y² – 3y – 2y + 6 = 0

⇒ y(y – 3) – 2(y – 3) = 0

⇒ (y – 3)(y – 2) = 0

⇒ y – 3 = 0 or y – 2 = 0

⇒ y = 3 or y = 2

Case I:

If y = 3, we get

x/(x + 1) = 3

⇒ x = 3(x + 1) [On cross multiplying]

⇒ x = 3x + 3

⇒ x = -3/2

Case II:

If y = 2, we get:

x(x + 1) = 2

⇒ x = 2(x + 1)

⇒ x = 2x + 2

⇒ - x = 2

⇒ x = -2

Hence, the roots of the equation are -3/2 and -2.

69. a/(x – b) + b(x – a) = 2, x ≠ b, a

Solution

a/(x – b) + b/(x – a) = 2

⇒ (a – x + b)[2x – (a + b)] = 0

⇒ a – x + b = 0 or 2x – (a + b) = 0

⇒ x = a + b or x = (a + b)/2

Hence, the roots of the equation are (a + b) and (a + b)/2.

70. a/(ax – 1) + b/(bx – 1) = (a + b), x ≠ 1/a, 1/b

Solution

a/(ax – 1) + b/(bx – 1) = (a + b)

⇒ [a/(ax – 1) – b] + [b/(bx – 1) – a] = 0

⇒ [a – b(ax – 1)/(ax – 1)] + [b – a(bx – 1)/(bx – 1)] = 0

⇒ (a – abx + b)/(ax – 1) + (a – abx + b)/(bx – 1) = 0

⇒ (a – abx + b)[1/(ax – 1) + 1/(bx – 1)] = 0

⇒ (a – abx + b)[(bx – 1) + (ax – 1)/(ax – 1)(bx – 1)] = 0

⇒ (a – abx + b)[(a + b)x – 2/(ax – 1)(bx – 1)] = 0

⇒ (a – abx + b)[(a + b)x – 2] = 0

⇒ a – abx + b = 0 or (a + b)x – 2 = 0

⇒ x = (a + b)/ab or x = 2/(a + b)

Hence, the roots of the equation are (a + b)/ab and 2/(a + b).

71. 3^{(x + 2)} + 3^-x = 10

Solution

3^{(x + 2)} + 3^-x = 10

3^x.9 + 1/3^x = 10

Let 3^x be equal to y.

∴ 9y + 1/y = 10

⇒ 9y² + 1 = 10y

⇒ 9y² – 10y + 1 = 0

⇒ (y – 1)(9y – 1) = 0

⇒ y – 1 = 0 or 9y – 1 = 0

⇒ y = 1 or y = 1/9

⇒ 3x^x = 1 or 3^x = 1/9

⇒ 3^x = 3⁰ or 3x = 3^-2

⇒ x = 0 or x = -2

Hence, 0 and -2 are the roots of the given equation.

72. 4^{(x +1)} + 4^{(1 – x)} = 10

Solution

Given:

4(x + 1) + 4(1 – x) = 10

⇒ 4^x .4 + 4¹.1/4⁴ = 10

Let 4^x be y.

∴ 4y + 4/y = 10

⇒ 4y² – 10y + 4 = 0

⇒ 4y² – 8y – 2y + 4 = 0

⇒ 4y(y – 2) – 2(y – 2) = 0

⇒ y = 2 or y = 2/4 = 1/2

⇒ 4x = 2 or 1/2

⇒ 4x = 22x or 21 or 22x = 2-1

⇒ x = ½ or x = -1/2

Hence, 1/2 and -1/2 are roots of the given equation.

73. 2^2x – 3.2^{(x + 2)} + 32 = 0

Solution

2^2x – 3.2^{(x + 2)} + 32 = 0

⇒ (2x)² – 3.2^x.2² + 32 = 0

Let 2^x be y.

∴ y² – 12y + 32 = 0

⇒ y² – 8y – 4y + 32 = 0

⇒ y(y – 8) – 4(y – 8) = 0

⇒ (y – 8) = 0 or (y – 4) = 0

⇒ y = 8 or y = 4

∴ 2x = 8 or 2x = 4

⇒ 2x = 23 or 2x = 22

⇒ x – 2 or 3

Hence, 2 and 3 are the roots of the given equation.