NCERT Exemplar Solutions for Class 10 Science Chapter 10 Light - Reflection and Refraction (MCQ, SAQ and LAQ)
Chapter Name | NCERT Exemplar Solutions for Class 10 Science Ch 10 Light - Reflection and Refraction |
Topics Covered |
|
Related Study |
|
Objective Type Questions for Light - Reflection and Refraction
1. Which of the following can make a parallel beam of light when light from a point source is incident on it?
(a) Concave mirror as well as convex lens
(b) Convex mirror as well as concave lens
(c) Two plane mirrors placed at 90° to each other
(d) Concave mirror as well as concave lens
Solution
(d) Concave mirror as well as concave lens
When point source of a light is focused to a convex or concave mirror emergent rays make a parallel beam of light.
2. A 10 mm long awl pin is placed vertically in front of a concave mirror. A 5 mm long image of the awl pin
is formed at 30 cm in front of the mirror. The focal length of this mirror is
(a) –30 cm
(b) –20 cm
(c) –40 cm
(d) –60 cm
Solution
(b) – 20 cm
Here, size of object = O = +10.0 mm = +1.0 cm (as, 1 cm = 10 mm)
Size of Image size = I = 5.0 mm = 0.5 cm
Image distance, v = −30 cm (as image is real)
Let, object distance = u
Focal length, f =?
Magnification m = I(size of image)/O (Size of image)
Magnification is given by m = -v/u
I/O = -v/u
0.5/1 = -30/u
U = -60 cm
Focal length is given by 1/f = 1/v + 1/u
1/f = 1/-30 + 1/-60
= (-2 - 1)/60
= -3/60
f = -20 cm
3. Under which of the following conditions a concave mirror can form an image larger than the actual
object?
(a) When the object is kept at a distance equal to its radius of curvature
(b) When object is kept at a distance less than its focal length
(c) When object is placed between the focus and centre of curvature
(d) When object is kept at a distance greater than its radius of curvature
Solution
(c) When object is placed between the focus and centre of curvature
When object is placed between F and C an enlarged image is formed beyond C.
4. Figure 10.1 shows a ray of light as it travels from medium A to medium B. Refractive index of the
medium B relative to medium A is
(a) √3/√2
(b) √2/√3
(c) 1/√2
(d)√2
Solution
(a) √3 / √2
Refractive Index of B with respect to A
= sin i/sin r
= sin60/sin45
= (√3/2)/1/√2
= √6/2
= 1.225
5. A light ray enters from medium A to medium B as shown in Figure 10.2. The refractive
index of medium B relative to A will be
(a) greater than unity
(b) less than unity
(c) equal to unity
(d) zero
(b) less than unity
(a) A rectangular glass slab
(b) A convex lens
(c) A concave lens
(d) A prism
(a) A rectangular glass slab
(a) Concave lens
(b) Rectangular glass slab
(c) Prism
(d) Convex lens
(a) Concave lens
(a) A convex lens has 4 dioptre power having a focal length 0.25 m
(b) A convex lens has –4 dioptre power having a focal length 0.25 m
(c) A concave lens has 4 dioptre power having a focal length 0.25 m
(d) A concave lens has –4 dioptre power having a focal length 0.25 m
(a) A convex lens has 4 dioptre power having a focal length 0.25 m
(a) is less than one
(b) is more than one
(c) is equal to one
(d) can be more than or less than one depending upon the position of the object in front of it
(a) is less than one
(a) 15 cm in front of the mirror
(b) 30 cm in front of the mirror
(c) between 15 cm and 30 cm in front of the mirror
(d) more than 30 cm in front of the mirror
(d) more than 30 cm in front of the mirror
Radius of curvature is double the focal length
hence c =30
When object is placed on c, its image is of the same size, inverted and is formed on c.
(a) a concave mirror
(b) a convex mirror
(c) a plane mirror
(d) both concave as well as plane mirror
(b) a convex mirror
(a) between the pole and the focus of the reflector
(b) very near to the focus of the reflector
(c) between the focus and centre of curvature of the reflector
(d) at the centre of curvature of the reflector
(b) very near to the focus of the reflector
(a) plane mirror only
(b) concave mirror only
(c) convex mirror only
(d) all mirrors irrespective of their shape
(d) all mirrors irrespective of their shape
(a) A
(b) B
(c) C
(d) D
(b) B
(a) Kerosene
(b) Water
(c) Mustard oil
(d) Glycerine
(d) Glycerine
Water-1.33
Kerosene-1.44
Mustard oil-1.46
Glycerine-1.47
Hence Glycerine is optically dense hence ray of light bends more with glycerine.
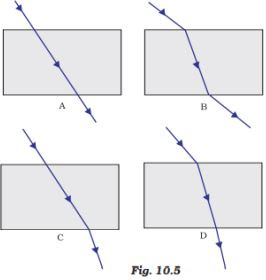
(b) Fig. B
(c) Fig. C
(d) Fig. D
(d) Fig. D
(a) Fig. A.
(b) Fig. B.
(c) Fig. C.
(d) Fig. D.
(a) Fig. A.
(a) Plane, convex and concave
(b) Convex, concave and plane
(c) Concave, plane and convex
(d) Convex, plane and concave
(c) Concave, plane and convex
(a) Concave mirror only
(b) Convex mirror only
(c) Convex lens only
(d) Concave mirror, convex mirror, concave lens and convex lens
(d) Concave mirror, convex mirror, concave lens and convex lens
Short Answer Questions for Light - Reflection and Refraction
(a) Object is placed between device and its focus, image formed is enlarged and behind it.
(b) Object is placed between the focus and device, image formed is enlarged and on the same side as that of the object.
(c) Object is placed between infinity and device, image formed is diminished and between focus and optical centre on the same side as that of the object.
(d) Object is placed between infinity and device, image formed is diminished and between pole and focus, behind it.
(a) Concave mirror
(b) Convex lens
(c) Concave lens
(d) Convex mirror
When light ray enters denser medium from rarer medium it bends towards the normal In this case extent of bending of ray at opposite parallel is same. Hence emergent ray is parallel to incident ray.
Bending of light here is a function of refraction. Refraction is dependent on refractive indices. Refractive indices of kerosene or turpentine would not be same as water. Hence degree of bend would be different in different mediums.
Refractive Index can be seen as the factor by which the speed and the wavelength of the radiation are reduced with respect to their vacuum values.
n = c/v
(where,
n = refractive index,
c = speed of light,
v = velocity of light in that medium)
Refractive index of one medium in relation to a second medium is given by ratio of speed of light. In second medium to speed of light in first medium.
Absolute RI of diamond = 1.6
Absolute RI of glass = 1.5
Multiplying them we get 2.4
When an object is placed in F and F2 of a convex lens, we get inverted, enlarged and real image is formed beyond 2F2 which is on the other side of the lens. Hence, we need to place the object between 20 and 40 cm of the lens. When an object is placed between F and 0 of a convex lens, its enlarged, erect and virtual image is formed beyond FL i.e. on the same side of lens. So for this we need to place the object at a distance less than 20 cm from the lens.
To obtain clear image of the building Sudha has to move the screen towards the lens. Focal length will be approximately 15 cm. The rays of light coming from distant object such as a tree (or a distant building or electricity pole) can be considered to be parallel to each other. When parallel rays of light are incident on a convex lens, the rays, after refraction, converge at focus on the other side of the lens.
Power of lens is inversely proportional to the focal length of the lens . Lens with focal length 20 has more power than lens with focal length 40 cm. Lens with higher power should be used to obtain more convergent light.
If two plane mirrors are placed perpendicular to each other then Incident ray and reflected ray will always be parallel to each other.
Speed of light decreases when it passes from rarer medium to denser medium and also light rays bend towards normal.
Long Answer Questions for Light - Reflection and Refraction
(b) between focus and centre of curvature of the mirror
(c) at centre of curvature of the mirror
(d) a little beyond centre of curvature of the mirror
(e) at infinity
(a) between optical centre and focus of the lens
(b) between focus and twice the focal length of the lens
(c) at twice the focal length of the lens
(d) at infinity
(e) at the focus of the lens
Laws of refraction
- Incident ray, refracted ray and normal at the point of incidence lie in the same plane.
- Ratio of sine of incidence and sine of refraction is constant for the given color and pair of media.

ABCD is a glass slab.
EF is incident ray which is incident on point O on air-glass interface.
- NO is normal and ∠ION= i1; which is the angle of incidence.
- OO’ is refracted ray from surface AD. It behaves like incident ray for surface BC.
- N’O’ and O’M’ are normal on surface BC.
- O’E is the emergent ray.
- ∠OO’N’ = i2; which is angle of incidence at surface BC.
- ∠EO’M’ = r2,; which is angle of refraction at surface BC.
- It is observed that the incident ray, the normal and the refracted ray lie in the same plane. This verifies the first law of refraction.
- It is also observed that IO is parallel to O’E; which means emergent ray is parallel to incident ray. This happens because the degree of bend at opposite surfaces of glass slab is same.
(a) at the focus of the lens
(b) between focus and twice the focal length of the lens
(c) beyond twice the focal length of the lens
(a) The ray diagram when the object is placed at the focus of the concave lens :

(b) The ray diagram when the object is placed between focus and twice the length of focal length of the lens:
(b) at finite distance from the mirror
(a) At Infinity
As the image is obtained on the screen , it is real .
so,
Magnification , m = –3 ,
v = 80 cm
u = ?
As m = v/u
so,
–3 = 80/u,
u = –80/3 cm .
From
1/f = 1/v - 1/u
= 1/80 + 3/80
= 4/80
= 1/20
1/f = 1/20cm
so, f = 20 cm .
The lens is convex and image formed at 80 cm from the lens is real and inverted.
m = 1/3
Using 1/𝑣 + 1/𝑢 = 1/𝑓
Calculate u; u = – 80 cm.
Image is real and inverted. Mirror is concave.
Degree of convergence and divergence provided by a lens is called power of the lens. Unit of power of lens is Diopter D.
focal length of lens used by first student is in positive hence it is a convex lens. The lens of second student is a concave lens.
p= 1/𝑓 = 1/0.5 = 2
Power of lens (first student) = +2
Power of lens (second student) = -2
Position of candle = 12.0 cm
Position of convex lens = 50.0 cm
Position of the screen = 88.0 cm
(i) What is the focal length of the convex lens?
(ii) Where will the image be formed if he shifts the candle towards the lens at a position of 31.0 cm?
(iv) Draw a ray diagram to show the formation of the image in case (iii) as said above.
Position of the candle flame = 12.0cm
Position of the lens = 50.0 cm
Position of the screen = 88.0 cm
Image distance v= 88-50= 38cm
Focal length = 1/𝑣 - 1/𝑢 = 1/𝑓
f= 19cm
(ii) Object distance u= 50-31= 19 cm
Here,
Object distance = focal length
Hence, the image is formed at infinity.
(iii) If he further shifts the candle towards the lens. The object comes between F and 0. In this case. Image is virtual, enlarged and erect and is formed on the same side of lens.