ICSE Revision Notes for Light Class 10 Physics
Chapter Name | Refraction of Light |
Topics Covered |
|
Related Study |
Refraction of Light
- The change in direction of the path of light when it passes from one transparent medium to another transparent medium is called refraction. The refraction of light is a surface phenomenon.
Experimental Observations
- When a ray of light travels from a rarer medium to a denser medium, it bends towards the normal, i.e. ∠i > ∠r. The deviation of the ray is δ = i − r.
- When a ray of light travels from a denser medium to a rarer medium, it bends away from the normal, i.e. ∠i < ∠r. The deviation of the ray is then δ = r − i.
- The ray of light which is incident normally on the surface separating the two media passes undeviated. Thus, if the angle of incidence ∠i = 0°, then the angle of refraction is ∠r = 0°. The deviation of the ray is zero.
Laws of Refraction
- The first law of refraction:
The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane. - Second law of refraction:
The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media and for a given wavelength of light. This law is also known as Snell’s law.
sin i/sin r = constant
1μ2 = 1n2
Speed of Light in a Medium and Refractive Index
- The extent of the change in the direction of light ray which occurs in a given pair of media is expressed in terms of the refractive index.
- Light travels the fastest in vacuum and also with almost the same speed in air, i.e. c = 3×108 ms−1.
- The refractive index of medium 2 with respect to medium 1 is given as
1μ2 = 1n2 = (Speed of light in medium)/(Speed of light in medium 2) = v1/v2 - Similarly, the refractive index of medium 1 with respect to medium 2 is
2μ1 = 2n1 = (Speed of light in medium 2)/(Speed of light in medium 1) = v2/v1 - If medium 1 is vacuum or air, then the refractive index of medium 2 is considered with respect to vacuum. This is known as the absolute refractive index of the medium.
μ = n = (Speed of light in vacuum)/(Speed of light in medium) = c/v - The absolute refractive index of a transparent medium is always greater than 1.
Conditions for no change in direction of light ray on refraction
- When the angle of incidence at the boundary of two media is zero.
- When the refractive index of medium 2 is the same as that of refractive index of medium 1.
Change in speed, direction and wavelength of light due to refraction
- Due to the change in the speed of light from one medium to another, the direction of the ray of light changes except for ∠i = 0°.
- When a ray of light passes from a rarer medium to a denser medium, its speed decreases. While if it passes from a denser to a rarer medium, its speed increases.
- Because the frequency of light depends on the source of light, it does not change on refraction.
- In refraction of light from one medium to another medium, due to the change in the speed of light, the wavelength of light also changes because its frequency remains unchanged.
Factors affecting the refractive index of a medium
- Nature of the medium, i.e. its optical density: Smaller the speed of light in a medium relative to air, higher is the refractive index of that medium.
- Physical condition such as temperature: With increase in temperature, the speed of light in the medium increases, so the refractive index of the medium decreases.
- The colour or wavelength of light: The speed of light of all colours is the same in air (or vacuum), but in any other transparent medium, the speed of light is different for different colours. In a medium, red light travels faster than violet light; therefore, the refractive index of a medium is more for violet light and less for red light. Thus, the refractive index of a medium increases with the decrease in wavelength.
Principle of Reversibility of the Path of Light
- According to this principle, the path of a light ray is reversible.
- A ray of light AO incident at an angle i on a plane surface SS' separating two media 1 and 2 is refracted along OB at an angle of refraction r.
- ∙ The refractive index of medium 2 with respect to medium 1 is
1μ2 = μ2/μ1 = sini/sinr = v1/v2 …(1) - Now, if refraction occurs from 2 to 1, then the principle of reversibility requires that the ray of light incident along BO at an angle of incidence r will be refracted only along OA at the angle of refraction i.
- The refractive index of medium 1 with respect to medium 2 is
2μ1 = μ1/μ2 = sini/sinr = v2/v1 …(2) - From equations (1) and (2), we get
1μ2 × 2μ1 = sini/sinr × sinr/sini = 1
∴ 2μ1 = 1/1μ2
OR 1μ2 = 1/2μ1
Refraction of Light through a Rectangular Glass Block
- Consider a rectangular glass block PQRS.
- A light ray AO falls on the surface PQ. NOM is the normal to the surface PQ at the point of incidence O. At the surface PQ, the ray AO travels from air to glass, so it bends towards the normal NOM and travels inside the glass in a straight line path along OB.
- At the surface RS, the ray OB suffers refraction again. N1BM1 is the normal to the surface RS at the point of incidence B.
- Ray OB travels from glass to air, so it bends away from the normal and travels along BC.
- The ray AO is called the incident ray, OB the refracted ray and BC the emergent ray. ∠AON is the angle of incidence i, ∠BOM is the angle of refraction r and ∠CBM1 is the angle of emergence e.
- Because refraction occurs at two parallel surfaces PQ and RS, ∠MOB = ∠N1BO and ∠i = ∠e, i.e. the angle of incidence i is equal to angle of emergence e by the principle of reversibility of the path of a light ray. Thus, the emergent ray BC is parallel to the incident ray AO.
Lateral Displacement
- Due to refraction of light through a parallel-sided glass block, the angle of incidence is equal to the angle of emergence, so the incident ray AO and the emergent ray BC are parallel, but they are not along the same line.
- The emergent ray is laterally displaced from the path of the incident ray. The path of the incident ray AO in the absence of a glass block is shown by the dotted line OD.
- The perpendicular distance XY between the path of the emergent ray and the direction of the incident ray is called lateral displacement.
Prism: Properties and Refraction
- A prism is a five-sided transparent medium with a triangular cross-section. Two opposite surfaces of the prism are identical parallel triangles, while the other three surfaces are rectangular and inclined on each other.
- A prism is a transparent refracting medium bounded by five plane surfaces inclined at some angles.
- The two rectangular plane inclined surfaces through which the light passes are called refracting surfaces. The angle between the two refracting surfaces is called the angle of prism.
- The line of intersection of the two refracting surfaces is called the refracting edge of the prism.
- The section of the prism perpendicular to the refracting edge is called the principal section of the prism.
- The third rectangular plane surface is the base of the prism.
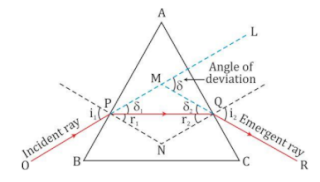
- The principal section ABC of a prism is shown below. The angle of the prism is ∠BAC = A.
- A monochromatic ray of light OP strikes the face AB of the prism at an angle of incidence i1. It suffers refraction making an angle of refraction r1 and travels along PQ inside the prism. Thus, PQ is the refracted ray.
- PQ strikes the face AC of the prism at an angle of incidence r2. It suffers refraction and emerges out of the prism as QR at an angle of emergence i2. Thus, QR is the emergent ray.
- Thus, the ray of light suffers refraction at two surfaces AB and AC of the prism.
- The angle between the direction of the incident ray (OP produced forward) and the emergent ray (QR produced backward) is called the angle of deviation. This is denoted by the Greek letter δ (delta).
From the figure, we have
∠LMQ = ∠MPQ + ∠MQP
∴ 𝛿 = ∠MPQ + ∠MQP
∴ 𝛿 = 𝛿1 + 𝛿2
The angle of incidence and the angle of emergence are
∠MPN = i1
∠MQN = i2
So, we have
∠MPQ = 𝛿1 = i1 – r1
∠MQQ = 𝛿2 = i2 – r2
∴ 𝛿 = i1 – r1 + i2 – r2
∴ 𝛿 = (i1 + i2) – (r1 + r2) ...(1)
For the quadrilateral APNQ,
∠APN = ∠AQN = 90°
∴ ∠PNQ +∠PAQ = 180° ...(2)
∴ ∠PNQ = 180° - A
However, in triangle PNQ, we have
∠PNQ = 180° - (r1 + r2) ...(3)
Thus, from equations (2) and (3), we have
A = r1 + r2 …(4)
Thus, from equations (1) and (4), we get
i1 + i2 = A + 𝛿
Factors affecting the angle of deviation
- 1Angle of incidence
- Material of the prism, i.e. on refractive index
- Angle of prism
- Colour or wavelength of light used
Real Depth and Apparent Depth
An object placed in a denser medium when viewed from a rarer medium appears to be at a depth less than its real depth. This is because of the refraction of light.
In the figure, for the incident ray OB, the angle of incidence i = ∠OBN' and the angle of refraction r = ∠CBN. Because AO and BN' are parallel and OB is a transversal line,
∠AOB = ∠OBN' = i
Similarly, IA' and BN are parallel and IC is the transversal line, so
∠BIA' = ∠CBN = r
Now, from the right-angled triangle BAO, we have
sin i = BA/OB
Similarly, in the right-angled triangle IAB, we have
sin r = BA/IB
From the definition of refractive index, we have
mμa = sin i /sinr = IB/OB
OR
aμm = 1/mμa = OB/IB
Because point B is close to A, we have IB = IA and OB = OA.
aμm = OA/IA = (Real depth)/(Apparent depth)
∴ Apparent depth = Real depth/aμm
Thus, we have the shift as
Shift = Real depth - Apparent depth
∴ Shift = Real depth (1 – 1/aμm)
Consequences of Refraction of Light
- A star appears to twinkle in the sky. Stars twinkle on account of atmospheric refraction. Starlight undergoes refraction many times before reaching the Earth.
- The apparent position of the star differs from the actual position due to refraction.
- The Sun is seen a few minutes before it rises above the horizon in the morning and a few minutes longer after it sets in the evening.
- A coin kept in a vessel and not visible when seen from just below the edge of the vessel can be viewed from the same position when water is poured into the vessel.
- A print appears to be raised when a glass block is placed over it.
- A tank appears shallow than its actual depth.
Critical Angle
- It is the angle of incidence in the denser medium corresponding to which the angle of refraction in the rarer medium is 90°.
1. When the angle of incidence is small, i.e. i < i
2. When the angle of incidence is equal to the critical angle, i.e. i = ic
3. When the angle of incidence is greater than the critical angle, i.e. i > ic
Critical Angle and Refractive Index
Consider the refraction of a light ray at a critical angle as shown in the following figure.
The refractive index of air with respect to glass is
gμa = sin ic/sin 90° = sin ic
However, we know that
aμg = 1/gμa = 1/sin ic = cosec ic
Factors Affecting the Critical Angle
- Colour (or wavelength) of light:
The refractive index of a transparent medium is most for violet light and least for red light; therefore, the critical angle for a pair of media is least for the violet light and most for the red light. Thus, the critical angle increases with increase in the wavelength of light. - Temperature:
On increasing the temperature of the medium, its refractive index decreases, so the critical angle for that pair of media increases. Thus, the critical angle increases with increase in temperature.
Total Internal Reflection
- ∙ When a ray of light travelling in a denser medium is incident at the surface of a rarer medium such that the angle of incidence is greater than the critical angle for the pair of media, the ray is totally reflected into the denser medium. This phenomenon is called total internal reflection.
|
Reflection from a plane mirror |
Total internal Reflection |
|
It occurs when light is incident on a plane mirror from any medium at any angle of incidence. |
It occurs when light passes from a denser medium to a rarer medium at an angle of incidence greater than the critical angle for that pair of media. |
|
Only a part of light is reflected while the rest is refracted and absorbed. |
The entire light is reflected. |
|
There is a loss of energy. The energy of the reflected light is less than that of the incident light. |
There is no loss of energy. The energy of the reflected light is the same as that of the incident light. |
|
The image is less bright and the brightness gradually decreases as silvering on mirror becomes old and rough. |
The image is much brighter and the brightness is permanent. |
Total Internal Reflection in a Prism
Total internal reflection through a 45°, 90°, 45° prism
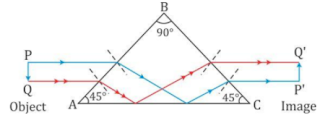
- A prism with an angle of 90° between its two refracting surfaces and the other two angles each equal to 45° is called a total reflecting prism because the light incident normally on any of its faces suffers total internal reflection inside the prism.
- This prism is used for the following three purposes:
1. To deviate a ray of light through 90°
2. To deviate a ray of light through 180°
3.. To erect an inverted image without deviation
Total internal reflection through a prism with each angle as 60°, i.e. an equilateral prism
- A prism with each angle of 60° can be used to deviate a light ray through 60° by total internal reflection.
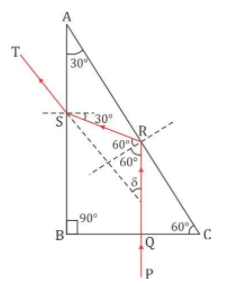
Total internal reflection and refraction through a 30°, 60°, 90° prism
1. Incident normally on face BC (side opposite to 30°)
- A phenomenon called mirage is observed on a hot dry day. In this phenomenon, a pool of water is observed on a road in front of a driver at some distance.
- A crack in glass is often seen shining like a mirror.
- A piece of diamond shines when viewed from certain directions.
- An optical fibre is used to transmit a light signal over a long distance with little loss of energy.