Frank Solutions for Chapter 21 Areas Theorem on Parallelograms Class 9 Mathematics ICSE
Exercise 21.1
1. ABCD is a parallelogram having an area of 60 cm2. P is a point on CD. Calculate the area of △APB.
Answer
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
Area (△APB) = (1/2)×60 cm2
We get,
Area (△APB) = 30 cm2
2. PQRS is a rectangle in which PQ = 12 cm and PS = 8 cm. Calculate the area of △PRS.
Answer
Hence,
PQ = SR
SR = 12 cm
PS = 8 cm
Area (△PRS) = (1/2)×base×height
Area (△PRS) = (1/2)×SR×PS
Area (△PRS) = (1/2)×12×8
We get,
Area (△PRS) = 48 cm2
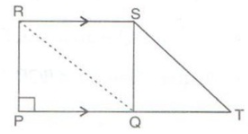
3. In the given figure area of || gm PQRS is 30 cm2. Find the height of || gm PQFE if PQ = 6 cm.
Answer:
(|| gm on same base PQ and between same parallel lines)
Therefore,
Area (|| gm PQFE) = 30 cm2
Base×Height = 30
⇒ 6×Height = 30
⇒ Height = 30/6
We get,
Height = 5 cm
Hence, the height of a parallelogram PQFE is 5 cm
4. In the given figure, ST || PR. Prove that: area of quadrilateral PQRS = area of △PQT
Answer
(Triangles on the same base PR and between the same parallel lines PR and ST)
Adding Area (△PQR) on both sides
We get,
Area (△PSR) + Area (△PQR) = Area (△PTR) + Area (△PQR)
⇒ Area (Quadrilateral PQRS) = Area (△PQT)
Hence, proved
5. In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 8 cm. Calculate the area of parallelogram ABCD.
Area (△APD) = (√3s2)/4
Area (△APD) = (√3×82)/4
Area (△APD) = (√3×64)/4
Area (△APD) = (√3×16)
On further calculation, we get,
Area (△APD) = 16√3 cm2
⇒ Area (△APD) = (1/2) ×area (parallelogram ABCD)
The area of a triangle is half that of a parallelogram on the same base and between the same parallels.
Area (parallelogram ABCD) = 2×area (△APD)
⇒ Area (parallelogram ABCD) = 2×16√3 cm2
We get,
Area (parallelogram ABCD) = 32√3 cm2
6. In the figure, if the area of ||gm PQRS is 84 cm2. Find the area of
(i) || gm PQMN
(ii) △PQS
(iii) △PQN
(i) Area of a rectangle and area of a parallelogram on the same base is equal
Here,
For rectangle PQMN, base is PQ
For parallelogram PQRS, base is PQ
Hence,
Area of rectangle PQMN = Area of parallelogram PQRS
Area of rectangle PQMN = 84 cm2
(ii) Area (△PQS) = (1/2)× area (parallelogram PQRS)
Area (△PQS) = (1/2)×84 cm2
We get,
Area (△PQS) = 42 cm2
(iii) Area (△PQN) = (1/2)× area (rectangle PQMN)
Area (△PQN) = (1/2)×84 cm2
We get,
Area (△PQN) = 42 cm2
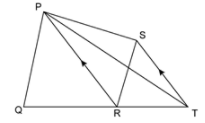
7.In the figure, PQR is a straight line. SQ is parallel to TP. Prove that the quadrilateral PQST is equal in area to the △PSR.
In quadrilateral PQST,
Area (△PQS) = (1/2) x area (quadrilateral PQST)
Area (quadrilateral PQST) = 2×area (△PQS) …(i)
In △PSR,
Area (△PSR) = area (△PQS) + area (△QSR)
Since QS is median as QS || TP
Hence,
Area (△PQS) = Area (△QSR)
Area (△PSR) = 2×area (△PQS) …(ii)
From equations (i) and(ii)
Area (quadrilateral PQST) = Area (△PSR)
Hence, proved
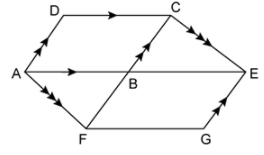
8. In the given figure, if AB || DC || FG and AE is a straight line. Also, AD || FC. Prove that: area of || gm ABCD = area of ||gm BFGE
By joining AC and FE
We get,
Area (△AFC) = Area (△AFE)
⇒ Area (△ABF) + Area (△ABC) = Area (△ABF) + Area (△BFE)
We get,
Area (△ABC) = Area (△BFE)
⇒ (1/2) Area (parallelogram ABCD) = (1/2) Area (parallelogram BFGE)
⇒ Area (parallelogram ABCD) = Area (parallelogram BFGE)
Hence, proved
9. In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.
Area of || gm PQRS = PQ×6
Also,
Area of || gm PQRS = PS×8
Therefore,
PQ ×6 = PS×8
⇒ PQ = (8PS)/6
We get,
PQ = (4PS)/3 …(i)
Perimeter of || gm PQRS = PQ + QR + RS + PS
42 = 2PQ + 2PS (Opposite sides of a parallelogram are equal)
⇒ 21 = PQ + PS
Substituting the value of PQ from equation (i), we get,
(4PS/3) + PS = 21
⇒ (4PS + 3PS)/3 = 21
⇒ 7PS = 63
We get,
PS = 9 cm
Now,
Substituting the value of PS in equation (i), we get,
PQ = (4PS)/3
⇒ PQ = (4×9)/3
We get,
PQ = 12 cm
Therefore, PQ = 12 cm and PS = 9 cm
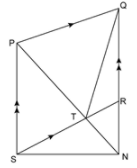
10. In the given figure, PT || QR and QT || RS. Show that: area of △PQR = area of △TQS.
By joining TR, we get,
Therefore,
Area (△PQR) = Area (△QTR) …(i)
△QTR and △TQS are on the same base QT and between the same parallel lines QT and RS
Therefore,
Area (△QTR) = Area (△TQS) …(ii)
From equations (i) and (ii), we get,
Area (△PQR) = Area (△TQS)
Hence, proved
11. In the given figure, △PQR is right – angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) △QRB ≅ △PQT
(b) Area of square PABQ = area of rectangle QTNM.
∠BQR = ∠BQP + ∠PQR
⇒ ∠BQR = 90° + ∠PQR
⇒ ∠PQT = ∠TQR + ∠PQR
⇒ ∠PQT = 90° + ∠PQR
Hence,
∠BQR = ∠PQT …(i)
(a) In △QRB and △PQT,
BQ = PQ …(sides of a square PABQ)
QR = QT …(sides of a square QRST)
∠BQR = ∠PQT …{From (i)}
Therefore,
△QRB ≅ △PQT (By SAS congruence criterion)
Area (△BQR) = Area (△PQT) …(ii)
(b) △PQT and rectangle QTNM are on the same base QT and between the same parallel lines QT and PN
Hence,
Area (△PQT) = (1/2) Area (rectangle QTNM)
Area (rectangle QTNM) = 2×Area (△PQT)
Area (rectangle QTNM) = 2×Area (△BQR) {from (ii)} …(iii)
△BQR and square PABQ are on the same base BQ and between the same parallel lines BQ and AR
Therefore,
2 ×Area (△BQR) = Area (square PABQ) …(iv)
From equations (iii) and (iv), we get,
Area (square PABQ) = Area (rectangle QTNM)
Hence, proved
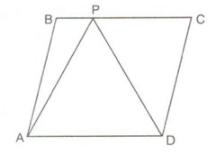
12. In the figure, AB = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.
In parallelogram ABCD,
Area (△ABC) = (1/2)×Area (parallelogram ABCD)
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
Area (parallelogram ABCD) = 2×Area (△ABC) …(i)
In △ACE,
Area (△ACE) = Area (△ABC) + Area (△BCE)
Since BC is median,
Hence,
Area (△ABC) = Area (△BCE)
Area (ACE) = 2×Area (△ABC) …(ii)
From equation
D is the midpoint
Area (△ABD) = Area (△ADC)
Hence, proved
13. Prove that the median of a triangle divides it into two triangles of equal area.
Answer
Since AD is median of △ABC
Hence,
D is the midpoint of BC
BD = DC
Multiplying by AL, we get,
BD ×AL = DC×AL
⇒ (1/2) (BD×AL) = (1/2) (DC×AL)
Therefore,
Area (△ABD) = Area (△ADC)
Hence, proved
14. AD is a median of a △ABC. P is any point on AD. Show that the area of △ABP is equal to the area of △ACP.
Answer
So, it will divide △ABC into two triangles of equal areas
Hence,
Area (△ABD) = Area (△ACD) …(i)
Now,
PD is the median of △PBC
Hence,
Area (△PBD) = Area (△PCD) …(ii)
On subtracting equation (ii) from equation (i), we get,
Area (△ABD) – Area (△PBD) = Area (△ACD) – Area (△PCD)
⇒ Area (△ABP) = Area (△ACP)
Hence, proved
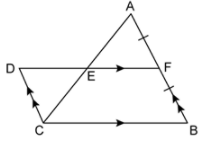
15. In the given figure AF = BF and DCBF is a parallelogram. If the area of △ABC is 30 square units, find the area of the parallelogram DCBF.
In △ABC,
AF = FB and EF || BC …(given)
Hence, AE = EC …(converse of mid-point theorem) …(i)
In △AEF and △CED,
∠FEA = ∠DEC …(vertically opposite angles)
CE = AE …{From (i)}
∠FAE = ∠DCE …(Alternate angles)
Therefore,
△AEF ≅ △CED (By ASA test of congruency)
Area (△AEF) = Area (△CED) …(ii)
⇒ Area (△ABC) = Area (△AEF) + Area (EFBC)
⇒ Area (△ABC) = Area (△CED) + Area (EFBC) ...{from (ii)}
Therefore,
Area (△ABC) = Area (parallelogram DCBF)
Hence, area of parallelogram DCBF is 30 square units
16. In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of △QTS is 60 cm2, find:
(i) the area of ||gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.
(i)
(ii)
(iii)
17. In the given figure, PQRS is a ||gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.
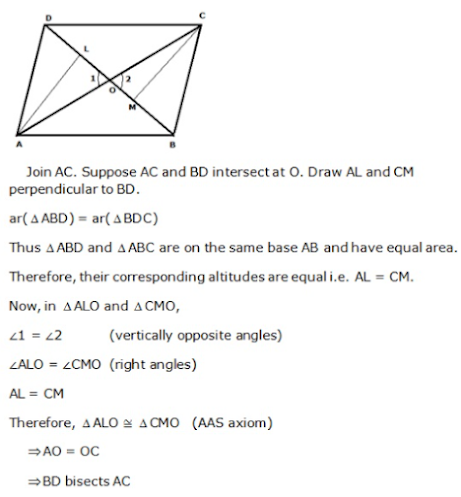
18. The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = 1/2 area of ||gm ABCD.
(ii) Area of APQD = Area of BPQC
Answer
19. The diagonals AC and BD of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of △ABC and △ADC are equal.
Answer
20. Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
Answer
21. PQRS is a parallelogram and
O is any point in its interior. Prove that:
Area(△POQ) + area(△ROS) = area(△QOR) + area(△SOP) = 1/2area(||gm PQRS)
Answer
22. A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
Answer
23. In the given figure, BC || DE,
(a) If area of △ADC is 20 sq. units, find the area of △AEB.
(b) If the area of △BFD is 8 square units, find the area of △CEF.
(a)
(b)
24. In the given figure, AB || SQ || DC and AD || PR || BC. If the area of quadrilateral ABCD is 24 square units, find the area quadrilateral PQRS.
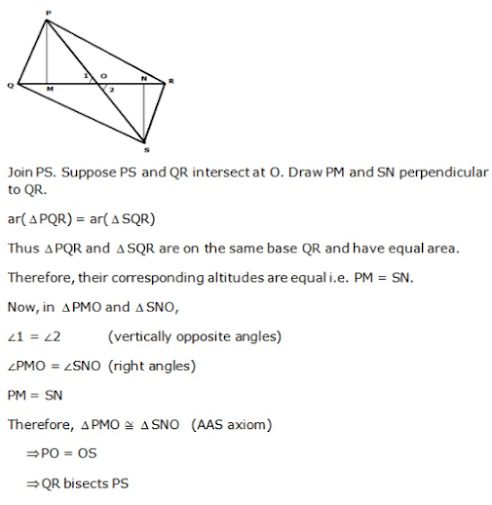
25. △PQR and △SQR are on the same base QR with P and S on opposite sides of line QR, such that area of △PQR is equal to the area of △SQR. Show that QR bisects PS.
Answer
26. If the medians of a △ABC intersect G, show that ar(△AGB) = ar(△AGC) = ar(△BGC) = 1/3ar(△ABC).
Answer
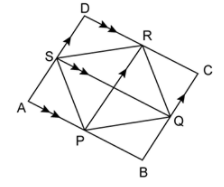
27. In △ABC, the mid-points of AB, BC and AC are P, Q and R respectively.
Prove that BQRP is a parallelogram and that its area is half of △ABC.
Answer
28. In the given figure, PQ || SR || MN, PS || QM and SM || PN. Prove that :
ar.(SMNT) = ar. (PQRS).
29. In △PQR, PS is a median. T is the mid-point of SR and M is the mid-point of PT. Prove that : △PMR = 1/8 △PQR.
Answer
30. In the figure, ABCD is a parallelogram and CP is parallel to DB. Prove that :
Area of OBPC = ¾ area of ABCD
31. The medians QM and RN of △PQR intersect at O. Prove that: area of △ROQ = area of quadrilateral PMON.
Answer
32. (a) In the given figure, ABC is a triangle and AD is the median.
Area of △ABE = Area of △ACE.
(b) In the given figure, ABC is a triangle and AD is the median.
If E is the midpoint of the median AD, prove that:
Area of △ABC = 4 × Area of △ABE
Answer
(a)
(b)
33. In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of △PMN is 20 square units, find the area of the parallelogram PQRS.
Answer
Construction: Join SM and SQ.
34. In a parallelogram PQRS, T is any point on the diagonal PR. If the area of △PTQ is 18 square units find the area of △PTS.
Answer
Construction: Join QR. Let the diagonals PR and QS intersect each other at point O.
35. ABCD is a quadrilateral in which diagonals AC and BD intersect at a point O. Prove that: area △AOD + area △BOC = area △ABO + area △CDO.
Answer
