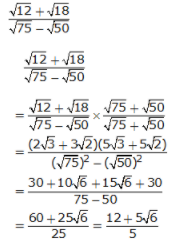Frank Chapter 1 Irrational Numbers ICSE Solutions Class 9 Math

Frank Solutions for Chapter 1 Irrational Numbers Class 9 Mathematics ICSE

Exercise 1.1

1. State which of these fractions have a terminating decimal.

(a) (3/ 5)

(b) (5 / 7)

(c) (25 / 49)

(d) (37 / 40)

(e) (57 / 64)

(f) (59 / 75)

(g) (89 / 125)

(h) (125 / 213)

(i) (147 / 160)

Answer

(a) (3/5)

5 = 1 × 5

⇒ 5 = 2⁰ × 5¹

i.e, 5 can be expressed as 2^m × 5ⁿ

Therefore,

(3/5) has terminating decimal representation

(b) (5/7)

7 = 1 × 7

i.e, 7 cannot be expressed a 2^m × 5ⁿ

Therefore,

(5/7) does not have terminating decimal representation

(c) (25/49)

49 = 7 × 7

i.e, 49 cannot be expressed as 2^m × 5ⁿ

Therefore,

(25/49) does not have terminating decimal representation

(d) (37/40)

40 = 2 × 2 × 2 × 5

⇒ 40 = 2³ × 5¹

i.e, 40 can be expressed as 2^m × 5ⁿ

Therefore,

(37/40) has terminating decimal representation

(e) (57 / 64)

64 = 2 × 2 × 2 × 2 × 2 × 2

⇒ 64 = 2⁶ × 5⁰

i.e, 64 can be expressed as 2^m × 5ⁿ

Therefore,

(57/64) has terminating decimal representation

(f) (59/75)

75 = 5 × 5 × 3

⇒ 75 = 5² × 3¹

i.e, 75 cannot be expressed as 2^m × 5ⁿ

Therefore,

(59/75) does not have terminating decimal representation

(g) (89/125)

125 = 5 × 5 × 5

⇒ 125 = 2⁰ × 5³

i.e, 125 can be expressed as 2^m × 5ⁿ

Therefore,

(89/125) has terminating decimal representation

(h) (125/213)

213 = 3 × 71

i.e, 213 cannot be expressed as 2^m × 5ⁿ

Therefore,

(125/213) does not have terminating decimal representation

(i) (147 / 160)

160 = 2 × 2 × 2 × 2 × 2 × 5

⇒ 160 = 2⁵ × 5¹

i.e, 160 can be expressed as 2^m × 5ⁿ

Therefore,

(147/160) has terminating decimal representation

2. Express each of the following decimals as a rational number

(a) 0.93

(b) 4.56

(c) 0.614

(d) 21.025

Answer

(a) 0.93 = 93 / 100

Hence,

The rational number of decimal 0.93 is (93 / 100)

(b) 4.56 = (456 / 100)

= (456 ÷ 4) / (100 ÷ 4)

We get,

= (114 / 25)

Hence,

The rational number of decimal 4.56 is (114 / 25)

(c) 0.614 = (614/1000)

= (614 ÷ 2)/(1000 ÷ 2)

We get,

= (307/500)

Hence,

The rational number of decimal 0.614 is (307/500)

(d) 21.025 = (21025/1000)

= (21025 ÷ 25)/(1000 ÷ 25)

We get,

= (841/40)

Hence,

The rational number of decimal 21.025 is (841/40)

3. Convert the following fractions into decimals:

(i) (3/5)

(ii) (8/11)

(iii) (-2/7)

(iv) (12/21)

(v) (13/25)

(vi) (2/3)

Answer

(i) (3/5)

(3/5) = 0.6

Hence,

The decimal form of (3/5) is 0.6

(ii) (8/11)

(8/11) = 0.72727272…..

(iii) (-2/7)

(-2/7) = -0.285714285714….

(iv) (12/21)

(12/21) = 0.571428571428……

(v) (13/25)

(13/25) = 0.52

Hence,

The decimal form of (13/25) is 0.52

(vi) (2/3)

(2/3) = 0.6666…..

⇒ (2/3) = 0.6

Hence,

The decimal form of (2/3) is 0.6

4. Express each of the following decimals as a rational number.

(a) 0.7

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Answer:

(a) 0.7

Let x = 0.7

Then,

x = 0.7777 ...(1)

Here, the number of digits recurring is only 1,

So, we multiply both sides of the equation (1) by 10

We get,

10x = 10 × 0.7777 …(2)

⇒ 10x = 7.777…..

On subtracting (1) from (2),

We get,

9x = 7

⇒ x = (7/9)

⇒ 0.7 = (7/9)

Therefore,

0.7 = (7/9)

(b) 

(c)

Here,

The number of digits recurring is 2,

So we multiply both sides of the equation (1) by 100

We get,

100x = 100 × 0.898989……

= 89.8989 …(2)

On subtracting (1) from (2),

We get,

99x = 89

(d) 

(e) 

(f) 

(g) 

Here, Only numbers 724 is being repeated.

So first, we need to remove 6 which proceeds 724

We multiply by 10 so that only the recurring digits remain after decimal

Thus,

10x = 10 × 4.6724724…….

⇒ 10x = 46. 724724 …(1)

The number of digits recurring in equation (1) is 3

Hence, we multiply both sides of the equation (1) by 1000

10000x = 1000 × 46.724724 = 46724.724 ...(2)

On subtracting (1) from (2), we get,

9990x = 46678

⇒ x = 46678 / 9990

We get,

x = 23339 / 4995

(h)

Here, only numbers 17 is being repeated, so first, we need to remove 0 which proceeds 17

We multiply by 10 so that only the recurring digits remain after the decimal,

Hence,

10x = 0.1717…(1)

The number of digits recurring in equation (1) is 2,

So we multiply both sides of the equation (1) by 100,

Hence,

1000x = 100 × 0.1717……..

= 17.1717….(2)

On subtracting (1) from (2),

We get,

990x = 17

(i) 

Here, only number 7 is being repeated, so first, we need to remove 02 which proceeds 7

We multiply by 100 so that only the recurring digits remain after decimal

Hence,

100x = 1702.7777…(1)

The number of digits recurring in equation (1) is 1,

So we multiply both sides of the equation (1) by 10

Hence,

1000x = 10 × 1702.7777……

= 17027.777…(2)

On subtracting (1) from (2),

We get,

900x = 15325

x = (15325 / 900)

5. Insert a rational number between:

(a) 2/5 and 3/4

(b) 3/4 and 5/7

(c) 4/3 and 7/5

(d) 5/9 and 6/7

Answer

(a) (2/5) and (3/4)

= [{(2/5) + (3/4)}/2]

On further calculation, we get,

= [{(8+15)/20}/2]

= {(23/20)/2}

We get,

= (23/40)

Therefore,

A rational number lying between (2/5) and (3/4) is (23/40)

(b) (3/4) and (5/7)

= [{(3/4) + (5/7)}/2]

On further calculation, we get,

= [{(21+20)/28}/2]

= {(41/28)/2}

We get,

= (41/56)

Therefore,

A rational number lying between (3/4) and (5/7) is (41/56)

(c) (4/3) and (7/5)

= [{(4/3) + (7/5)}/2]

On further calculation, we get,

= [{(20 + 21)/15}/2]

= {(41/15)/2}

We get,

= (41/30)

Therefore,

A rational number lying between (4/3) and (7/5) is (41/30)

(d) (5/9) and (6/7)

= [{(5/9) + (6/7)}/2]

On further calculation, we get,

= [{(35 + 54)/63}/2]

= {(89/63)/2}

We get,

= (89/126)

Therefore,

A rational number lying between (5/9) and (6/7) is (89/126)

6. State, whether the following numbers are rational or irrational:

(a) (3 + √3)²

(b) (5 – √5)²

(c) (2 + √2) (2 – √2)

(d) {(√5) / (3√2)}²

Answer:

(a) (3 + √3)²

= (3)² + (√3)² + 2×3×√3

On calculating further, we get,

= 9 + 3 + 6√3

= 12 + 6√3

which is a rational number

Therefore,

(3 + √3)² is a rational number

(b) (5 – √5)²

= (5)² + (√5)² – 2×5×√5

On further calculation, we get,

= 25 + 5 – 10√5

= 30 – 10√5

which is a irrational number

Therefore,

(5 – √5)² is an irrational number

(c) (2 + √2) (2 – √2)

= (2)² – (√2)²

= 4 – 2

= 2

which is a rational number

Therefore,

(2 + √2) (2 – √2) is a rational number

(d) {(√5)/(3√2)}²

= {(5)/(9×2)}

We get,

= 5/18

which is a rational number

Therefore,

{√5/(3√2)}² is a rational number

7. Check whether the square of the following is rational or irrational:

(a) 3√2

(b) 3 + √2

(c) (3√2) / 2

(d) √2 + √3

Answer

(a) 3√2

(3√2)²

= 9 × 2

= 18

which is a rational number

Hence,

The square of (3√ 2) is a rational number

(b) 3 + √2

(3 + √2)²

= (3)² + (√2)² + 2×3×√2

On further calculation, we get,

= 9 + 2 + 6√2

= 11 + 6√2

which is irrational number

Hence,

The square of (3 + √2) is an irrational number

(c) (3√2)/2

{(3√2)/2}²

= (9×2)/4

= (9/2)

which is a rational number

Hence,

The square of {(3√2)/2} is a rational number

(d) √2 + √3

(√2+√3)²

= (√2)² + (√3)² + 2×√2×√3

= 2 + 3 + 2√6

We get,

= 5 + 2√6

which is irrational number

Hence,

The square of (√2 + √3) is an irrational number

8. Show that √5 is an irrational number. (Use division method)

Answer

Here,

Clearly, √5 = 2.23606…… is an irrational number

Therefore,

√5 is an irrational number

9. Without using division method show that √7 is an irrational number

Answer

Let √7 be a rational number

Hence,

√7 = (a / b)

On squaring both sides, we get,

7 = (a² / b²)

a² = 7b²

Since, a² is divisible by 7, a is also divisible by 7…(1)

Let a = 7c

On squaring both sides, we get,

a² = 49c²

Substituting a² = 7b²

We get,

7b² = 49c²

b² = 7c²

Since, b² is divisible by 7, b is also divisible by 7…(2)

From (1) and (2) we can observe that both a and b are divisible by 7

i.e, a and b have a common factor 7

This contradicts our assumption that (a/b) is rational number

i.e, a and b do not have any common factor other than unity (1)

Hence,

(a/b) is not rational number

√7 is not rational number

Therefore,

√7 is an irrational number

10. Write a pair of irrational numbers

(a) (√3 + 5) and (√5 – 3) whose sum is irrational

(b) (√3 + 5) and (4 – √3) whose sum is rational

(c) (√3 + 2) and (√2 – 3) whose difference is irrational

(d) (√5 – 3) and (√5 + 3) whose difference is rational

(e) (5 + √2) and (√5 – 2) whose product is irrational

(f) (√3 + √2) and (√3 – √2) whose product is rational

Answer

(a) Given

(√3 + 5) and (√5 – 3) are irrational numbers whose sum is irrational

Thus,

We have,

(√3 + 5) + (√5 – 3)

= √3 + 5 + √5 – 3

We get,

= √3 + √5 + 2

which is irrational number

(b) Given,

(√3 + 5) and (4 – √3) are irrational numbers whose sum is rational

Thus,

We have,

(√3 + 5) + (4 – √3)

= √3 + 5 + 4 – √3

We get,

= 9

which is a rational number

(c) Given

(√3 + 2) and (√2 – 3) are irrational numbers whose difference is irrational

Thus,

We have,

(√3 + 2) – (√2 – 3)

= √3 + 2 – √2 + 3

We get,

= √3 – √2 + 5

which is irrational

(d) Given

(√5 – 3) and (√5 + 3) are irrational numbers whose difference is rational

Thus,

We have,

(√5 – 3) – (√5 + 3)

= √5 – 3 – √5 – 3

We get,

= -6

which is a rational number

(e) Given

(5 + √2) and (√5 – 2) are irrational numbers whose product is irrational

Thus,

We have,

(5 + √2) (√5 – 2)

= 5 (√5 – 2) + √2 (√5 – 2)

We get,

= 5√5 – 10 + √10 – 2√2

-which is irrational numbers

(f) Given

(√3 + √2) and (√3 – √2) are irrational numbers whose product is rational

Thus,

We have,

(√3 + √2) (√3 – √2)

= (√3)² – (√2)²

= 3 – 2

We get,

= 1

which is a rational number

11. Simplify by rationalizing the denominator in each of the following:

(a) (3√2) / √5

(b) {1 / (5 + √2)}

(c) {1 / (√3 + √2)}

(d) {2 / (3 + √7)}

(e) {5 / (√7 – √2)}

(f) {42 / (2√3 + 3√2)}

(g) {(√3 + 1) / (√3 – 1)}

(h) (√5 – √7) / √3

(i) (3 – √3) / (2 + √2)

Answer

(a) (3√2)/√5

= {(3√2)/√5} × (√5)/(√5)

On simplification, we get,

= {(3√2) × √5}/(√5)²

We get,

= (3√10)/5

(b) {1/(5 + √2)}

= {1/(5 + √2)} × {(5 – √2)/(5 – √2)}

On simplification, we get,

= (5 – √2) / (5)² – (√2)²

= (5 – √2) / (25 – 2)

We get,

= (5 – √2)/23

(c) {1/(√3 + √2)}

= {1/(√3 + √2)} × (√3 – √2)/(√3 – √2)

On simplification, we get,

= (√3 – √ 2)/(√3)² – (√2)²

= (√3 – √2)/(3 – 2)

= (√3 – √2)/1

We get,

= (√3 – √2)

(d) {2/(3 + √7)}

= {2/(3 + √7)} × (3 – √7)/(3 – √7)

On further calculation, we get,

= {2 (3 – √7)}/(3)² – (√7)²

= {2(3 – √7)}/(9 – 7)

= {2(3 – √7)}/2

We get,

= (3 – √7)

(e) {5/(√7 – √2)}

= {5/(√7 – √2)} × (√7 + √2)/(√7 + √2)

On further calculation, we get,

= {5(√7 + √2)}/(√7)² – (√2)²

= {5(√7 + √2)}/(7 – 2)

= {5(√7 + √2)}/5

We get,

= (√7 + √2)

(f) {42/(2√3 + 3√2)}

= {42/(2√3 + 3√2)} × {(2√3 – 3√2)/(2√3 – 3√2)}

= {42 (2√3 – 3√2)}/(2√3)² – (3√2)²

On further calculation, we get,

= (84√3 – 126√2)/(4 × 3) – (9 × 2)

= (84√3 – 126√2)/(12 – 18)

= (84√3 – 126√2)/-6

= -14√3 + 21√2

= 21√2 – 14√3

We get,

= 7(3√2 – 2√3)

(g) {(√3 + 1)/(√3 – 1)}

= (√3 + 1)/(√3 – 1) × (√3 + 1)/(√3 + 1)

On further calculation, we get,

= (√3 + 1)²/(√3)² – (1)²

= {(√3)² + 2×√3×1 + (1)²}/(3 – 1)

= (3 + 2√3 + 1)/2

= (4 + 2√3)/2

We get,

= 2 + √3

(h) (√5 – √7)/√3

= {(√5 – √7)/√3} × (√3)/(√3)

= (√5×√ 3 – √7×√ 3)/(√3)²

We get,

= (√15 – √21)/3

(i) (3 – √3)/(2 + √2)

= (3 – √3)/(2 + √2) × (2 – √2)/(2 – √2)

= {3(2 – √2) – √3 (2 – √2)}/(2)² – (√2)²

On further calculation, we get,

= (6 – 3√2 – 2√3 + √6)/(4 – 2)

= (6 – 3√2 – 2√3 + √6)/2

12. Simplify by rationalizing the denominator in each of the following:

(i) (5 + √6)/(5 – √6)

(ii) (4 + √8)/(4 – √8)

(iii) (√15 + 3)/(√15 – 3)

(iv) (√7 – √5)/(√7 + √5)

(v) (3√5 + √7)/(3√5 – √7)

(vi) (2√3 – √6)/(2√3 + √6)

(vii) (5√3 – √15)/(5√3 + √15)

(viii) (2√6 – √5)/(3√5 – 2√6)

(ix) (7√3 – 5√2)/(√48 + √18)

(x) (√12 + √18)/(√75 – √50)

Answer

(i) (5 + √6)/(5 – √6)

= (5 + √6)/(5 – √6) × (5 + √6)/(5 + √6)

On further calculation, we get,

= (5 + √6)²/(5)² – (√6)²

= {(5)² + 2×5×√6 + (√6)²}/(25 – 6)

= (25 + 10√6 + 6)/19

We get,

= (31 + 10√6)/19

(ii) (4 + √8)/(4 – √8)

= (4 + √8)/(4 – √8) × (4 + √8)/(4 + √8)

On further calculation, we get,

= (4 + √8)²/(4)² – (√8)²

= {(4)² + 2×4×√8 + (√8)²}/(16 – 8)

= (16 + 8√8 + 8)/(16 – 8)

= (24 + 8√8)/8

We get,

= 3 + √8

(iii) (√15 + 3)/(√15 – 3)

= (√15 + 3)/(√15 – 3) × (√15 + 3)/(√15 + 3)

= (√15 + 3)²/(√15)² – (3)²

= {(√15)² + 2×√15×3 + (3)²}/(15 – 9)

On further calculation, we get,

= (15 + 6√15 + 9)/6

= (24 + 6√15)/6

We get,

= 4 + √15

(iv) (√7 – √5)/(√7 + √5)

= (√7 – √5)/(√7 + √5) × (√7 – √5)/(√7 – √5)

= (√7 – √5)²/(√7)² – (√5)²

On further calculation, we get,

= (7 + 5 – 2√35)/(7 – 5)

= (12 – 2√35)/2

We get,

= 6 – √35

(v) (3√5 + √7)/(3√5 – √7)

= (3√5 + √7)/3√5 – √7) × (3√5 + √7)/(3√5 + √7)

= (3√5 + √7)²/(3√5)² – (√7)²

On further calculation, we get,

= {(3√5)² + (√7)² + 2 × 3√5 × √7}/(45 – 7)

= (45 + 7 + 6√35)/38

= (52 + 6√35)/38

We get,

= (26 + 3√35)/19

(vi) (2√3 – √6)/(2√3 + √6)

= (2√3 – √6)/(2√3 + √6) × (2√3 – √6)/(2√3 – √6)

= (2√3 – √6)²/(2√3)² – (√6)²

On further calculation, we get,

= {(2√3)² + (√6)² – 2×2√3 ×√6}/(4×3 – 6)

= (12 + 6 – 4√18)/(12 – 6)

= (18 – 4√18)/6

= (9 – 2√18)/3

= (9 – 6√2)/3

We get,

= 3 – 2√2

(vii) (5√3 – √15)/(5√3 + √15)

= (5√3 – √15)/5√3 + √15) × (5√3 – √15)/(5√3 – √15)

= (5√3 – √15)²/(5√3)² – (√15)²

On further calculation, we get,

= (75 + 15 – 10√45)/(75 – 15)

= (90 – 10√45)/60

= (9 – 1√45)/6

= (9 – 3√5)/6

We get,

= (3 – √5)/2

(viii) (2√6 – √5)/(3√5 – 2√6)

= (2√6 – √5)/(3√5 – 2√6) × (3√5 + 2√6)/(3√5 + 2√6)

On simplification, we get,

= (6√30 + 24 – 15 – 2√30)/(3√5)² – (2√6)²

= (6√30 + 9 – 2√30)/(45 – 24)

We get,

= (4√30 + 9)/21

(ix) (7√3 – 5√2)/(√48 + √18)

= (7√3 – 5√2)/(√48 + √18) × (√48 – √18)/(√48 – √18)

On simplification, we get,

= (7√144 – 7√54 – 5√96 + 5√36)/(√48)² – (√18)²

= (84 – 21√6 – 20√6 + 30)/(48 – 18)

We get,

= (114 – 41√6)/30

(x) (√12 + √18)/(√75 – √50)

= (√12 + √18)/(√75 – √50) × (√75 + √50)/(√75 + √50)

On further calculation, we get,

= {(2√3 + 3√2) (5√3 + 5√2)}/ (√75)² – (√50)²

= (30 + 10√6 + 15√6 + 30)/(75 – 50)

= (60 + 25√6)/25

We get,

= (12 + 5√6)/5

13. Simplify each of the following:

(i) 3 / (5 – √3) + 2 / (5 + √3)

(ii) (4 + √5) / (4 – √5) + (4 – √5) / (4 + √5)

(iii) (√5 – 2)/(√5 + 2) – (√5 + 2)/(√5 – 2)

(iv) (√7 – √3)/(√7 + √3) – (√7 + √3)/(√7 – √3)

(v) (√5 + √3)/ √5 – √3) + (√5 – √3) / √5 + √3)

Answer

(i) 3/(5 – √3) + 2/(5 + √3)

= {3(5 + √3) + 2(5 – √3)}/(5 – √3) (5 + √3)

On simplification, we get,

= (15 + 3√3 + 10 – 2√3)/(5)² – (√3)²

= (25 + √3)/(25 – 3)

We get,

= (25 + √3)/22

(ii) (4 + √5)/(4 – √5) + (4 – √5)/(4 + √5)

= {(4 + √5)² + (4 – √5)²}/(4 – √5) (4 + √5)

On simplification, we get,

= (16 + 5 + 8√5 + 16 + 5 – 8√5)/(4)² – (√5)²

= (21 + 21)/(16 – 5)

We get,

= (42/11)

(iii) (√5 – 2)/(√5 + 2) – (√5 + 2)/(√5 – 2)

= (√5 – 2)² – (√5 + 2)²}/(√5 + 2) (√5 – 2)

On simplification, we get,

= (5 + 4 – 4√5 – 5 – 4 – 4√5)/(√5)² – (2)²

= –8√5 /(5 – 4)

We get,

= –8√5

(iv) (√7 – √3)/(√7 + √3) – (√7 + √3)/(√7 – √3)

= (√7 – √3)² – (√7 + √3)²/(√7 + √3) (√7 – √3)

On simplification, we get,

= (7 + 3 – 2√21 – 7 – 3 – 2√21)/(√7)² – (√3)²

= – 4√21/(7 – 3)

= (- 4√21)/4

We get,

= –√21

(v) (√5 + √3)/ √5 – √3) + (√5 – √3)/√5 + √3)

= (√5 + √3)² + (√5 – √3)²/(√5 – √3) (√5 + √3)

On simplification, we get,

= (5 + 3 + 2√15 + 5 + 3 – 2√15)/(5 – 3)

= 16/2

We get,

= 8

14. Simplify the following:

(i) √6/(√2 + √3) + 3√2/(√6 + √3) – 4√3/(√6 + √2)

(ii) 3√2/(√6 – √3) – 4√3/(√6 – √2) + 2√3/(√6 + 2)

(iii) 6/(2√3 – √6) + √6/(√3 + √2) – 4√3/(√6 – √2)

(iv) 7√3/(√10 + √3) – 2√5/(√6 + √5) – 3√2/(√15 + 3√2)

(v) 4√3/(2 – √2) – 30/(4√3 – 3√2) – 3√2/(3 + 2√3)

Answer

(i) √6/(√2 + √3) + 3√2/(√6 + √3) – 4√3/(√6 + √2)

Rationalizing the denominator of each term, we have

= {√6 (√2 – √3)/(√2 + √3) (√2 – √3)} + {(3√2 (√6 – √3)/(√6 + √3) (√6 – √3)}- {(4√3 (√6 – √2)/(√6 + √2) (√6 – √2)}

On further calculation, we get,

= {(√12 – √18)/(2 – 3)} + {(3√12 – 3√6)/(6 – 3)} – {(4√18 – 4√6)/(6 – 2)}

= {(√12 – √18)/-1} + {(3√12 – 3√6)/3} – {(4√18 – 4√6)/4}

= √18 – √12 + √12 – √6 – √18 + √6

We get,

= 0

(ii) 3√2/(√6 – √3) – 4√3/(√6 – √2) + 2√3/(√6 + 2)

Rationalizing the denominator of each term, we have,

= {3√2(√6 + √3)/(√6 – √3) (√6 + √3)} – {(4√3 (√6 + √2)/(√6 – √2) (√6 + √2)} + {(2√3 (√6 – 2)/(√6 + 2) (√6 – 2)}

On further calculation, we get,

= {(3√12 + 3√6)/(6 – 3)} – {(4√18 + 4√6)/(6 – 2)} + {(2√18 – 4√3)/(6 – 4)}

= {(3√12 + 3√6)/3} – {(4√18 + 4√6)/4} + {(2√18 – 4√3)/2}

= √12 + √6 – √18 – √6 + √18 – 2√3

= √12 – 2√3

= 2√3 – 2√3

We get,

= 0

(iii) 6 / (2√3 – √6) + √6 / (√3 + √2) – 4√3 / (√6 – √2)

Rationalizing the denominator of each term, we have

= {6 (2√3 + √6)/(2√3 – √6) (2√3 + √6)} + {(√6 (√3 – √2)/(√3 + √2) (√3 – √2)} – {(4√3 (√6 + √2)/(√6 – √2) (√6 + √2)

On simplification, we get,

= (12√3 + 6√6) / (12 – 6) + (√18 – √12)/(3 – 2) – (4√18 + 4√6)/(6 – 2)

= {(12√3 + 6√6)/6} + {(√18 – √12)/1} – {(4√18 + 4√6)/4}

= 2√3 + √6 + √18 – √12 – √18 – √6

= 2√3 – √12

= 2 √3 – 2√3

We get,

= 0

(iv) 7√3/(√10 + √3) – 2√5/(√6 + √5) – 3√2/(√15 + 3√2)

Rationalizing the denominator of each term, we have,

= {7√3 (√10 – √3)/(√10 + √3) (√10 – √3)} – {2√5 (√6 – √5)/(√6 + √5) (√6 – √5)} – {3√2 (√15 – 3√2)/(√15 + 3√2) (√15 – 3√2)

= {(7√30 – 21)/(10 – 3)} – {(2√30 – 10)/(6 – 5)} – {(3√30 – 18)/(15 – 18)}

= (7√30 – 21)/7 – (2√30 – 10)/1 – (3√30 – 18)/-3

= (7√30 – 21)/7 – (2√30 – 10)/1 + (3√30 – 18)/3

= √30 – 3 – 2√30 + 10 + √30 – 6

We get,

= 1

(v) 4√3/(2 – √2) – 30/(4√3 – 3√2) – 3√2/(3 + 2√3)

Rationalizing the denominator of each term, we have,

= {(4√3 (2 + √2)/(2 – √2) (2 + √2)} – {30 (4√3 + 3√2)/(4√3 – 3√2) (4√3 + 3√2)} – {(3√2 (3 – 2√3)/(3 + 2√3) (3 – 2√3)

= {(8√3 + 4√6)/(4 – 2)} – {(120√3 + 90√2)/(48 – 18)} – {(9√2 – 6√6)/(9 – 12)}

= {(8√3 + 4√6)/2} – {120√3 + 90√2)/30} – {(9√2 – 6√6)/-3}

= {(8√3 + 4√6)/2} – {(120√3 + 90√2)/30} + {(9√2 – 6√6)/3}

= 4√3 + 2√6 – 4√3 – 3√2 + 3√2 – 2√6

We get,

= 0

15. If (√2.5 – √0.75)/(√2.5 + √0.75) = p + q√30, find the values of p and q.

Answer

Given

(√2.5 – √0.75)/(√2.5 + √0.75)

= {(√2.5 – √0.75)/(√2.5 + √0.75)} × {(√2.5 – √0.75)/(√2.5 – √0.75)}

= (√2.5 – √0.75)²/(√2.5)² – (√0.75)²

On simplification, we get,

= (2.5 – 2×√2.5×√0.75 + 0.75)/(2.5 – 0.75)

= (3.25 – 2×√0.25×10×√0.25×3)/1.75

= (3.25 – 2 × 0.25√30)/1.75

= (3.25 – 0.5√30)/1.75

= (3.25)/(1.75) – (0.5)/(1.75) √30

= (325/175) – (50/175) √30

= (13/7) – (2/7)√30

= (13/7) + (- 2/7) √30

= p + q√30

Therefore,

The value of p = (13/7) and q = (-2/7)

Exercise 1.2

1. State, whether the following numbers are rational or irrational.

(a) (3 + √3)²

(b) (5 - √5)²

(c) (2 + √2)(2 - √2)

(d) [√5/(3√2)]²

Answer

(a)

(b)

(c)

(d)

2. Check whether the square of the following is rational or irrational.

(a) 3√2

(b) 3 + √2

(c) (3√2)/2

(d) √2 + √3

Answer

(a)

(b) 

(c)

(d)

3. Show that √5 is an irrational numbers. [Use division method]

Answer

4. Without using division method show that √7 is an irrational numbers.

Answer

5. (a) Write a pair of irrational numbers whose sum is irrational.

(b) Write a pair of irrational whose sum is rational.

(c) Write a pair of irrational numbers whose difference is irrational.

(d) Write a pair of irrational numbers whose difference is rational.

(e) Write a pair of irrational number whose product is irrational.

(f) Write a pair of irrational numbers whose product is rational.

Answer

(a) (√3 + 5) and (√5 – 3) are irrational numbers whose sum is irrational.

Thus, we have

(√3 + 5) + (√5 - 3)

= √3 + 5 + √5 – 3

= √3 + √5 + 2, which is irrational.

 (b) 

(c) 

(d)

(e) 

(f) 

6. Compare the following:

(a) ∜12 and ∛15

(b) ∛48 and √36

Answer

(a)

(b)

7. (a) Write the following in ascending order:

2√5, √3 and 5√2

(b) Write the following in ascending order.

2∛3, 4∛3 and 3∛3

(c) Write the following in ascending order:

5√7, 7√5 and 6√2

(d) Write the following in ascending order:

7∛5, 6∛4, 5∛6

Answer

(a)

(b)

(c)

(d)

8. (a) Write the following in descending order:

√2, ∛5 and ∜10

(b) Write the following in descending order:

5√3, √15 and 3√5

(c) Write the following in descending order:

√6, ∛8 and ∜3

Answer

(a)

(b)

(c)

9. Insert two irrational numbers between 3 and 4.

Answer

10. Insert five irrational numbers between 2√3 and 3√5.

Answer

11. Write two numbers between √3 and √7.

Answer

12. Write four rational numbers between √2 and √3.

Answer

13. State which of the following are surds. Give reasons. 
(a) √150

(b) ∛4

(c) ∛50.∛20

(d) ∛-27
(e) √(2+√3)

(f)

Answer

(a)

(b)

(c)

(d)

(e)

(f)

14. Represent the number √7 on the number line.

Answer

Exercise 1.3 

1. Simplify by rationalizing the denominator in each of the following:

(a)  (3√2)/√5

(b) 1/(5+√2)

(c) 1/(√3+√2)

(d) 2/(3+√7)

(e) 5/(√7-√2)

(f) 42/(2√3 + 3√2)

(g) (√3+1)/(√3–1)

(h) (√5-√7)/√3

(i) (3-√3)/(2+√2)

Answer

(a)

(b) 

(c) 

(d) 

(e) 

(f) 

(g)

(h) 

(i) 

2. Simplify by rationalizing the denominator in each of the following:

(i) (5 + √6)/(5 - √6)

(ii) (4 + √8)/(4 - √8)

(iii) (√15+3)/(√15-3)

(iv) (√7 - √5)/(√7 + √5)

(v) (3√5 + √7)/(3√5 - √7)

(vi) (2√3 - √6)/(2√3 + √6)

(vii) (5√3 - √15)/5√3 + √15)

(viii) (2√6 - √5)/(3√5 - 2√6)

(ix) (7√3 - 5√2)/(√48 + √18)

(x) (√12+√18)/(√75-√50)

Answer

(i) 

(ii) 

(iii) 

(iv) 

(v) 

(vi) 

(vii) 

(viii) 

(ix) 

(x) 

3. Simplify each of the following:

(i) 3/(5 - √3) + 2/(5 + √3)

(ii) (4 + √5)/(4 - √5) + (4 - √5)/(4 + √5)

(iii) (√5 – 2)/(√5 + 2) – (√5 + 2)/(√5 – 2)

(iv) [(√7 - √3)/(√7 + √3)] – [(√7 + √3)/(√7 - √3)]

(v) (√5 + √3)/(√5 - √3) + (√5 - √3)/(√5 + √3)

Answer

(i)

(ii)

(iii)

(iv) 

(v) 

4. Simplify the following:

(i) √6/(√2+√3) + 3√2/(√6+√3) - 4√3/(√6+√2)

(ii) 3√2/(√6-√3) - 4√3/(√6-√2) + 2√3/(√6 + 2)

(iii) 6/(2√3-√6) + √6/(√3+√2) - 4√3/(√6-√2)

(iv) 7√3/(√10+√3) - 2√5/(√6+√5) - 3√2/(√15 + 3√2)

(v) 4√3/(2-√2) – 30/(4√3 - 3√2) - 3√2/(3 + 2√3)

Answer

(i)

(ii) 

(iii) 

(iv) 

(v) 

5. If (√2.5 - √0.75)/(√2.5 + √0.75) = p+ q√30, find the values of p and q.

Answer

6. In each of the following, find the values of a and b.

(a)  (√3 – 1)/(√3 + 1) = (a + b√3)

(b) (3 + √7)/(3 - √7) = a + b√7

(c) (5 + 2√3)/(7 + 4√3) = a + b√3

(d) 1/(√5 - √3) = (8√5 - b√3)

(e) (√3 – 2)/(√3 + 2) = 8√3 + b

(f) (√11 - √7)/(√11 + √7) = a - b√77

(g) (7√3 - 5√2)/(4√3 + 3√2) = a - b√6

(h) (√2 + √3)/(3√2 - 2√3) = (a - b√6)

(i) (7 + √5)/(7 - √5) – (7 - √5)/(7 + √5) = a + b√5

(j) (√3 – 1)/(√3 + 1) + (√3 + 1)(√3 – 1) = a + b√3

Answer

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

(j) 

7. If x = (7 + 4√3), find the values of

(i) √x + 1/√x

(ii) x² + 1/x²

(iii) x³ + 1/x³

(iv) If x = (7 + 4√3), find the values of: (x + 1/x)²

Answer

(i) 

(ii)

(iii) 

(iv) 

8. If x = (4 - √15), find the values of

(i) 1/x,

(ii) x + 1/x

(iii) x² + 1/x² 

(iv) x³ + 1/x³

(v) If x = (4 - √15), find the values of: (x + 1/x)²

Answer

(i)

(ii)

(iii)

(iv)

(v)

9. If x = (2 + √5)/(2 - √5) and y = (2 - √5)/(2 + √5), show that (x² – y²) = 144√5.

Answer

10. If x = (√3 + 1)/(√3 – 1) and y = (√3 – 1)/(√3 + 1), find the values of

(i) x² + y²,

(ii) x³ + y³, and

(iii) x² – y² + xy

Answer

(i)

(ii)

(iii)

11. If x = 1/(3 - 2√2) and y = 1/(3 + 2√2), find the values of

(i) x² + y²,

(ii) x³ + y³

Answer

(i)

(ii)