Selina Concise Solutions for Chapter 16 Understanding Shapes Class 8 ICSE Mathematics
Exercise 16A
1. State which of the following are polygons:
Solution
Only Fig. (ii), (iii) and (v) are polygons.
Fig. (ii) and (iii) are concave polygons while
Fig. (v) is convex.
2. Calculate the sum of angles of a polygon with :
(i) 10 sides
(ii) 12 sides
(iii) 20 sides
(iv) 25 sides
Solution
(i) No. of sides n = 10
sum of angles of polygon = (n – 2)×180°
= (10 – 2)× 180° = 1440°
(ii) no. of sides n = 12
sum of angles = (n – 2)×180°
= (12 – 2)×180° = 10×180° = 1800°
(iii) n = 20
Sum of angles of Polygon = (n – 2)× 180°
= (20 – 2)× 180° = 3240°
(iv) n = 25
Sum of angles of polygon = (n – 2)× 180°
= (25 – 2)× 180° = 4140°
3. Find the number of sides in a polygon if the sum of its interior angles is :
(i) 900°
(ii) 1620°
(iii) 16 right-angles
(iv) 32 right-angles.
Solution
(i) Let no. of sides = n
Sum of angles of polygon = 900˚
(n – 2) × 180˚ = 900˚
⇒ n – 2 = 900/180
⇒ n – 2 = 5
⇒ n = 5 + 2
⇒ n = 7
(ii) Let no. of sides = n
Sum of angles of polygon = 1620˚
(n – 2) × 180˚ = 1620˚
⇒ n – 2 = 1620/180
⇒ n – 2 = 9
⇒ n = 9 + 2
⇒ n = 11
(iii) Let no. of sides = n
Sum of angles of polygon = 16 right = 16 × 90 = 1440˚
(n – 2) × 180˚ = 1440˚
⇒ n – 2 = 1440/180˚
⇒ n – 2 = 8
⇒ n = 8 + 2
⇒ n = 10
(iv) Let no. of sides = n
Sum of angles of polygon = 32 right angles = 32 × 90 = 2880˚
(n × 2) × 180˚ = 2880
n – 2 = 2880/180
n – 2 = 16
n = 16 + 2
n =18
4. Is it possible to have a polygon; whose sum of interior angles is :
(i) 870°
(ii) 2340°
(iii) 7 right-angles
(iv) 4500°
Solution
(i) Let no. of sides = n
Sum of angles = 870°
(n – 2) × 180° = 870°
⇒ n – 2 = 870/180
⇒ n – 2 = 29/6
⇒ n = 29/6 + 2
⇒ n = 41/6
Which is not a whole number.
Hence it is not possible to have a polygon, the sum of whose interior angles is 870°
(ii) Let no. of sides = n
Sum of angles = 2340°
(n – 2) × 180° = 2340°
⇒ n – 2 = 2340/180
⇒ n – 2 = 13
⇒ n = 13 + 2 = 15
Which is a whole number.
Hence it is possible to have a polygon, the sum of whose interior angles is 2340°.
(iii) Let no. of sides = n
Sum of angles = 7 right angles = 7 ×90 = 630°
(n – 2) × 180° = 630°
⇒ n – 2 = 630/180
⇒ n – 2 = 7/2
⇒ n = 7/2 + 2
⇒ n = 11/2
Which is not a whole number. Hence it is not possible to have a polygon, the sum of whose interior angles is 7 right-angles.
(iv) Let no. of sides = n
(n – 2)×180° = 4500°
⇒ n – 2 = 4500/180
⇒ n – 2 = 25
⇒ n = 25 + 2
⇒ n = 27
Which is a whole number.
Hence it is possible to have a polygon, the sum of whose interior angles is 4500°.
5. (i) If all the angles of a hexagon are equal; find the measure of each angle.
(ii) If all the angles of a 14-sided figure are equal; find the measure of each angle.
Solution
(i) No. of sides of hexagon, n = 6
Let each angle be = x°
Sum of angles = 6x°
(n – 2)× 180° = Sum of angles
⇒ (6 – 2)× 180° = 6x°
⇒ 4× 180 = 6x
⇒ x = (4 × 180)/6
⇒ x = 120˚
∴ Each angle of hexagon = 120˚
(ii) No. of sides of polygon, n = 14
Let each angle = x˚
∴ Sum of angles = 14x˚
∴ (n – 2) × 180˚ = Sum of angles of polygon
∴ (14 – 2) × 180˚ = 14x
12 × 180˚ = 14x
⇒ x = (12 × 180)/14
⇒ x = 1080/7
⇒ x = (154 2/7)˚
6. Find the sum of exterior angles obtained on producing, in order, the sides of a polygon with :
(i) 7 sides
(ii) 10 sides
(iii) 250 sides.
Solution
(i) No. of sides n = 7
Sum of interior & exterior angles at one vertex = 180°
Sum of interior & exterior angles = 7 × 180˚
= 1260˚
Sum of interior angles = (n – 2) × 180˚
= (7 – 2) × 180˚
= 900˚
∴ Sum of exterior angles = 1260˚ - 900˚
= 360˚
(ii) No. of sides n = 10
Sum of interior and exterior angles = 10 × 180˚
= 1800˚
But sum of interior angles = (n – 2) × 180˚
= (10 – 2) × 180˚
= 1440˚
∴ Sum of exterior angles = 1800 – 1440
= 360˚
(iii) No. of sides n = 250
Sum of all interior and exterior angles = 250 × 180˚
= 45000˚
But sum of interior angles = (n – 2) × 180˚
= (250 – 2) × 180˚
= 248 × 180˚
= 44640˚
∴ Sum of exterior angles = 45000 – 44640
= 360˚
7. The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x – 1)°, (10x + 2)°, (8x + 2)° (9x – 3)°, (5x + 4)° and (12x + 6)° ; find each exterior angle.
Solution
Sum of exterior angles of hexagon formed by producing sides of order = 360°
∴ (6x – 1)˚ - (10x + 2)˚ + (8x + 2)˚ + (9x – 3)˚ + (5x + 4)˚ + (12x + 6)˚ = 360˚
50x + 10˚ = 360˚
⇒ 50x = 360˚ - 10˚
⇒ 50x = 350˚
⇒ x = 350/70
⇒ x = 7
∴ Angles are (6x – 1)˚ : (10x + 2)˚ : (8x + 2)˚ : (9x – 3)˚ : (5x + 4)˚ and (12x + 6)˚
i.e. (6 × 7 – 1)˚ : (10 × 7 + 2)˚ : (8 × 7 + 2)˚ : (9 × 7 – 3)˚ : (5 × 7 + 4)˚ : (12 × 7 + 6)˚
i.e. 41° ; 72°, 58° ; 60° ; 39° and 90°
8. The interior angles of a pentagon are in the ratio 4: 5: 6: 7: 5. Find each angle of the pentagon.
Solution
Let the interior angles of the pentagon be 4x, 5x, 6x, 7x, 5x.
Their sum = 4x + 5x + 6x + 7x + 5x = 21x
Sum of interior angles of a polygon = (n – 2) × 180˚
= (5 – 2) × 180˚
= 540˚
∴ 27x = 540
⇒ x = 540/27
⇒ x = 20˚
∴ Angles are 4 × 20˚ = 80˚
5 × 20˚ = 100˚
6 × 20˚ = 120˚
7 × 20˚ = 140˚
5 × 20˚ = 100˚
⇒ n – 2 = 900/180
⇒ n – 2 = 5
⇒ n = 5 + 2
⇒ n = 7
(ii) Let no. of sides = n
Sum of angles of polygon = 1620˚
(n – 2) × 180˚ = 1620˚
⇒ n – 2 = 1620/180
⇒ n – 2 = 9
⇒ n = 9 + 2
⇒ n = 11
(iii) Let no. of sides = n
Sum of angles of polygon = 16 right = 16 × 90 = 1440˚
(n – 2) × 180˚ = 1440˚
⇒ n – 2 = 1440/180˚
⇒ n – 2 = 8
⇒ n = 8 + 2
⇒ n = 10
(iv) Let no. of sides = n
Sum of angles of polygon = 32 right angles = 32 × 90 = 2880˚
(n × 2) × 180˚ = 2880
n – 2 = 2880/180
n – 2 = 16
n = 16 + 2
n =18
4. Is it possible to have a polygon; whose sum of interior angles is :
(i) 870°
(ii) 2340°
(iii) 7 right-angles
(iv) 4500°
Solution
(i) Let no. of sides = n
Sum of angles = 870°
(n – 2) × 180° = 870°
⇒ n – 2 = 870/180
⇒ n – 2 = 29/6
⇒ n = 29/6 + 2
⇒ n = 41/6
Which is not a whole number.
Hence it is not possible to have a polygon, the sum of whose interior angles is 870°
(ii) Let no. of sides = n
Sum of angles = 2340°
(n – 2) × 180° = 2340°
⇒ n – 2 = 2340/180
⇒ n – 2 = 13
⇒ n = 13 + 2 = 15
Which is a whole number.
Hence it is possible to have a polygon, the sum of whose interior angles is 2340°.
(iii) Let no. of sides = n
Sum of angles = 7 right angles = 7 ×90 = 630°
(n – 2) × 180° = 630°
⇒ n – 2 = 630/180
⇒ n – 2 = 7/2
⇒ n = 7/2 + 2
⇒ n = 11/2
Which is not a whole number. Hence it is not possible to have a polygon, the sum of whose interior angles is 7 right-angles.
(iv) Let no. of sides = n
(n – 2)×180° = 4500°
⇒ n – 2 = 4500/180
⇒ n – 2 = 25
⇒ n = 25 + 2
⇒ n = 27
Which is a whole number.
Hence it is possible to have a polygon, the sum of whose interior angles is 4500°.
5. (i) If all the angles of a hexagon are equal; find the measure of each angle.
(ii) If all the angles of a 14-sided figure are equal; find the measure of each angle.
Solution
(i) No. of sides of hexagon, n = 6
Let each angle be = x°
Sum of angles = 6x°
(n – 2)× 180° = Sum of angles
⇒ (6 – 2)× 180° = 6x°
⇒ 4× 180 = 6x
⇒ x = (4 × 180)/6
⇒ x = 120˚
∴ Each angle of hexagon = 120˚
(ii) No. of sides of polygon, n = 14
Let each angle = x˚
∴ Sum of angles = 14x˚
∴ (n – 2) × 180˚ = Sum of angles of polygon
∴ (14 – 2) × 180˚ = 14x
12 × 180˚ = 14x
⇒ x = (12 × 180)/14
⇒ x = 1080/7
⇒ x = (154 2/7)˚
6. Find the sum of exterior angles obtained on producing, in order, the sides of a polygon with :
(i) 7 sides
(ii) 10 sides
(iii) 250 sides.
Solution
(i) No. of sides n = 7
Sum of interior & exterior angles at one vertex = 180°
Sum of interior & exterior angles = 7 × 180˚
= 1260˚
Sum of interior angles = (n – 2) × 180˚
= (7 – 2) × 180˚
= 900˚
∴ Sum of exterior angles = 1260˚ - 900˚
= 360˚
(ii) No. of sides n = 10
Sum of interior and exterior angles = 10 × 180˚
= 1800˚
But sum of interior angles = (n – 2) × 180˚
= (10 – 2) × 180˚
= 1440˚
∴ Sum of exterior angles = 1800 – 1440
= 360˚
(iii) No. of sides n = 250
Sum of all interior and exterior angles = 250 × 180˚
= 45000˚
But sum of interior angles = (n – 2) × 180˚
= (250 – 2) × 180˚
= 248 × 180˚
= 44640˚
∴ Sum of exterior angles = 45000 – 44640
= 360˚
7. The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x – 1)°, (10x + 2)°, (8x + 2)° (9x – 3)°, (5x + 4)° and (12x + 6)° ; find each exterior angle.
Solution
Sum of exterior angles of hexagon formed by producing sides of order = 360°
∴ (6x – 1)˚ - (10x + 2)˚ + (8x + 2)˚ + (9x – 3)˚ + (5x + 4)˚ + (12x + 6)˚ = 360˚
50x + 10˚ = 360˚
⇒ 50x = 360˚ - 10˚
⇒ 50x = 350˚
⇒ x = 350/70
⇒ x = 7
∴ Angles are (6x – 1)˚ : (10x + 2)˚ : (8x + 2)˚ : (9x – 3)˚ : (5x + 4)˚ and (12x + 6)˚
i.e. (6 × 7 – 1)˚ : (10 × 7 + 2)˚ : (8 × 7 + 2)˚ : (9 × 7 – 3)˚ : (5 × 7 + 4)˚ : (12 × 7 + 6)˚
i.e. 41° ; 72°, 58° ; 60° ; 39° and 90°
8. The interior angles of a pentagon are in the ratio 4: 5: 6: 7: 5. Find each angle of the pentagon.
Solution
Let the interior angles of the pentagon be 4x, 5x, 6x, 7x, 5x.
Their sum = 4x + 5x + 6x + 7x + 5x = 21x
Sum of interior angles of a polygon = (n – 2) × 180˚
= (5 – 2) × 180˚
= 540˚
∴ 27x = 540
⇒ x = 540/27
⇒ x = 20˚
∴ Angles are 4 × 20˚ = 80˚
5 × 20˚ = 100˚
6 × 20˚ = 120˚
7 × 20˚ = 140˚
5 × 20˚ = 100˚
9. Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.
Solution
Two angles of a hexagon are 120°, 160°
Let remaining four angles be x, x, x and x.
Their sum = 4x + 280°
But sum of all the interior angles of a hexagon
= (6 – 2) × 180˚
= 4 × 180˚
= 720˚
∴ 4x + 280˚ = 720˚
⇒ 4x = 720˚ - 280˚
Solution
Two angles of a hexagon are 120°, 160°
Let remaining four angles be x, x, x and x.
Their sum = 4x + 280°
But sum of all the interior angles of a hexagon
= (6 – 2) × 180˚
= 4 × 180˚
= 720˚
∴ 4x + 280˚ = 720˚
⇒ 4x = 720˚ - 280˚
⇒ 4x = 440˚
⇒ x = 110˚
∴ Equal angles are 110˚ (each)
10. The figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B: ∠C : ∠D = 5: 6: 7.
(iii) Find angles B, C and D.
Solution
(i) Sum of interior angles of the pentagon
= (5 – 2) × 180˚
= 3 × 180˚ = 540˚ [∵ sum for a polygon of x sides = (x – 2) × 180˚]
(ii) Since AB ∥ ED
∴ ∠A + ∠E = 180˚
(iii) Let ∠B = 5x ∠C = 6x ∠D = 7x
∴ 5x + 6x + 7x + 180˚ = 540˚ (∠A + ∠E = 180˚) Proved in (ii)
⇒ 18x = 540˚ - 180˚
⇒ 18x = 360˚
⇒ x = 20˚
⇒ x = 110˚
∴ Equal angles are 110˚ (each)
10. The figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B: ∠C : ∠D = 5: 6: 7.
(i) Using formula, find the sum of interior angles of the pentagon.
(ii) Write the value of ∠A + ∠E(iii) Find angles B, C and D.
Solution
(i) Sum of interior angles of the pentagon
= (5 – 2) × 180˚
= 3 × 180˚ = 540˚ [∵ sum for a polygon of x sides = (x – 2) × 180˚]
(ii) Since AB ∥ ED
∴ ∠A + ∠E = 180˚
(iii) Let ∠B = 5x ∠C = 6x ∠D = 7x
∴ 5x + 6x + 7x + 180˚ = 540˚ (∠A + ∠E = 180˚) Proved in (ii)
⇒ 18x = 540˚ - 180˚
⇒ 18x = 360˚
⇒ x = 20˚
∴ ∠B = 5 × 20˚ = 100˚,
∠C = 6 × 20˚ = 120˚
∠D = 7 × 20 = 140˚
11. Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
Solution
Let number of sides = n
Sum of interior angles = (n – 2) × 180˚
= 180n - 360˚
Sum of 2 right angles = 2 × 90˚
= 180˚
∴ Sum of other angles = 180˚n - 360˚ - 180˚
= 180˚n - 540˚
No. of vertices at which these angles are formed = n – 2
∴ Each interior angle = (180n – 540)/(n – 2)
∴ (180n – 540)/(n – 2) = 120˚
⇒ 180n – 540 = 120n – 240
⇒ 180n – 120n = -240 + 540
⇒ 60n = 300
⇒ n = 300/60
⇒ n = 5
12. In a hexagon ABCDEF, side AB is parallel to side FE and ∠B: ∠C: ∠D: ∠E = 6 : 4: 2: 3. Find ∠B and ∠D.
Solution
Given: Hexagon ABCDEF in which AB∥ EF and ∠B: ∠C: ∠D: ∠E = 6: 4: 2 : 3.
To find: ∠B and ∠D
Proof: No. of sides n = 6
∴ Sum of interior angles = (n – 2) × 180˚
= (6 – 2) × 180˚
= 720˚
∵ AB ∥ EF (Given)
∴ ∠A + ∠F = 180˚
But ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720˚ (Proved)
∠B + ∠C + ∠D + ∠E + ∠180˚ = 720˚
∴ ∠B + ∠C + ∠D + ∠E = 720˚ - 180˚ = 540˚
Ratio = 6 : 4 : 2 : 3
Sum of parts = 6 + 4 + 2 + 3 = 15
∴ ∠B = 6/15 × 540 = 216˚
∠D = 2/15 × 540 = 72˚
Hence, ∠B = 216˚; ∠D = 72˚
13. The angles of a hexagon are x + 10°, 2x + 20°, 2x – 20°, 3x – 50°, x + 40° and x + 20°. Find x.
Solution
Angles of a hexagon are x + 10˚, 2x + 20˚, 2x - 20˚, 3x - 50˚, x + 40˚ and x + 40˚ and x + 20˚
∴ But sum of angles of a hexagon = (x – 2) × 180˚
= (6 – 2) × 180˚
= 4 × 180˚
= 720˚
But sum = x + 10 + 2x + 20˚ + 2x - 20˚ + 3x - 50˚ + x + 40 + x + 20
= 10x + 90 – 70
= 10x + 20
∴ 10x + 20 = 720˚
⇒ 10x = 72 - 20 = 700
⇒ x = 700˚/10 = 70˚
∴ x = 70˚
14. In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3: 7. Find the biggest angle of the pentagon.
Solution
In a pentagon, two angles are 40° and 60° Sum of remaining 3 angles = 3× 180°
= 540° – 40° – 60° = 540° – 100° = 440°
Ratio in these 3 angles =1 : 3 : 7
Sum of ratios =1 + 3 + 7 = 11
Biggest angle = (440 × 7)/11 = 280°
∠D = 7 × 20 = 140˚
11. Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
Solution
Let number of sides = n
Sum of interior angles = (n – 2) × 180˚
= 180n - 360˚
Sum of 2 right angles = 2 × 90˚
= 180˚
∴ Sum of other angles = 180˚n - 360˚ - 180˚
= 180˚n - 540˚
No. of vertices at which these angles are formed = n – 2
∴ Each interior angle = (180n – 540)/(n – 2)
∴ (180n – 540)/(n – 2) = 120˚
⇒ 180n – 540 = 120n – 240
⇒ 180n – 120n = -240 + 540
⇒ 60n = 300
⇒ n = 300/60
⇒ n = 5
12. In a hexagon ABCDEF, side AB is parallel to side FE and ∠B: ∠C: ∠D: ∠E = 6 : 4: 2: 3. Find ∠B and ∠D.
Solution
To find: ∠B and ∠D
Proof: No. of sides n = 6
∴ Sum of interior angles = (n – 2) × 180˚
= (6 – 2) × 180˚
= 720˚
∵ AB ∥ EF (Given)
∴ ∠A + ∠F = 180˚
But ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720˚ (Proved)
∠B + ∠C + ∠D + ∠E + ∠180˚ = 720˚
∴ ∠B + ∠C + ∠D + ∠E = 720˚ - 180˚ = 540˚
Ratio = 6 : 4 : 2 : 3
Sum of parts = 6 + 4 + 2 + 3 = 15
∴ ∠B = 6/15 × 540 = 216˚
∠D = 2/15 × 540 = 72˚
Hence, ∠B = 216˚; ∠D = 72˚
13. The angles of a hexagon are x + 10°, 2x + 20°, 2x – 20°, 3x – 50°, x + 40° and x + 20°. Find x.
Solution
Angles of a hexagon are x + 10˚, 2x + 20˚, 2x - 20˚, 3x - 50˚, x + 40˚ and x + 40˚ and x + 20˚
∴ But sum of angles of a hexagon = (x – 2) × 180˚
= (6 – 2) × 180˚
= 4 × 180˚
= 720˚
But sum = x + 10 + 2x + 20˚ + 2x - 20˚ + 3x - 50˚ + x + 40 + x + 20
= 10x + 90 – 70
= 10x + 20
∴ 10x + 20 = 720˚
⇒ 10x = 72 - 20 = 700
⇒ x = 700˚/10 = 70˚
∴ x = 70˚
14. In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3: 7. Find the biggest angle of the pentagon.
Solution
In a pentagon, two angles are 40° and 60° Sum of remaining 3 angles = 3× 180°
= 540° – 40° – 60° = 540° – 100° = 440°
Ratio in these 3 angles =1 : 3 : 7
Sum of ratios =1 + 3 + 7 = 11
Biggest angle = (440 × 7)/11 = 280°
Exercise 16 B
1.Fill in the blanks :
In case of regular polygon, with :
Solution
Explanation
(i) Each exterior angle = 360˚/8 = 45˚
Each interior angle = 180˚ - 45˚ = 135˚
(ii) Each exterior angle = 360˚/12 = 30˚
Each interior angle = 180˚ - 30˚ = 150˚
(iii) Since each exterior = 72˚
∴ Number of sides = 360˚/72˚ = 5
Also interior angle = 180˚ - 72˚ = 108˚
(iv) Since each exterior angle = 45˚
∴ Number of sides = 360˚/45˚ = 8
Interior angle = 180˚ - 45˚ = 135˚
(v) Since interior angle = 150˚
∴ Exterior angle = 180˚ - 150˚ = 30˚
∴ Number of sides = 360˚/30˚ = 12
(vi) Since interior angle = 140˚
∴ Exterior angle = 180˚ - 140˚ = 40˚
∴ Number of sides = 360˚/40˚ = 9
2. Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 135°
(iii) 1 1/5 of a right-angle
Solution
(i) Let no. of sides of regular polygon be n.
Each interior angle = 160˚
∴ (n – 2)/n × 180˚ = 360˚
⇒ 180˚n - 360˚ = 160n
⇒ 20n = 360˚
⇒ n = 18
(ii) No. of sides = n
Each interior angle = 135˚
(n – 2)/n × 180˚ = 135˚
⇒ 180n - 360˚ = 135n
⇒ 180n – 135n = 360˚
⇒ 45n = 360˚
⇒ n = 8
(iii) No. of sides = n
Each interior angle = 1 1/5 right angles
= 6/5 × 90˚
= 108˚
∴ (n – 2)/n × 180˚ = 108˚
⇒ 180n – 360 ˚ = 108n
⇒ 180n -108n = 360˚
⇒ 72n = 360˚
⇒ n = 5
In case of regular polygon, with :
Explanation
(i) Each exterior angle = 360˚/8 = 45˚
Each interior angle = 180˚ - 45˚ = 135˚
(ii) Each exterior angle = 360˚/12 = 30˚
Each interior angle = 180˚ - 30˚ = 150˚
(iii) Since each exterior = 72˚
∴ Number of sides = 360˚/72˚ = 5
Also interior angle = 180˚ - 72˚ = 108˚
(iv) Since each exterior angle = 45˚
∴ Number of sides = 360˚/45˚ = 8
Interior angle = 180˚ - 45˚ = 135˚
(v) Since interior angle = 150˚
∴ Exterior angle = 180˚ - 150˚ = 30˚
∴ Number of sides = 360˚/30˚ = 12
(vi) Since interior angle = 140˚
∴ Exterior angle = 180˚ - 140˚ = 40˚
∴ Number of sides = 360˚/40˚ = 9
2. Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 135°
(iii) 1 1/5 of a right-angle
Solution
(i) Let no. of sides of regular polygon be n.
Each interior angle = 160˚
∴ (n – 2)/n × 180˚ = 360˚
⇒ 180˚n - 360˚ = 160n
⇒ 20n = 360˚
⇒ n = 18
(ii) No. of sides = n
Each interior angle = 135˚
(n – 2)/n × 180˚ = 135˚
⇒ 180n - 360˚ = 135n
⇒ 180n – 135n = 360˚
⇒ 45n = 360˚
⇒ n = 8
(iii) No. of sides = n
Each interior angle = 1 1/5 right angles
= 6/5 × 90˚
= 108˚
∴ (n – 2)/n × 180˚ = 108˚
⇒ 180n – 360 ˚ = 108n
⇒ 180n -108n = 360˚
⇒ 72n = 360˚
⇒ n = 5
3. Find the number of sides in a regular polygon, if its each exterior angle is :
(i) 1/3 of a right angle
(ii) two-fifth of a right-angle.
Solution
(i) Each exterior angle = 1/3 of a right angle
= 1/3 ×90
= 30°
Let number of sides = n
∴ 360˚/n = 30˚
∴ n = 360˚/30˚
⇒ n = 12
(ii) Each exterior angle = 2/5 of a right-angle
= 2/5 × 90˚
(i) 1/3 of a right angle
(ii) two-fifth of a right-angle.
Solution
(i) Each exterior angle = 1/3 of a right angle
= 1/3 ×90
= 30°
Let number of sides = n
∴ 360˚/n = 30˚
∴ n = 360˚/30˚
⇒ n = 12
(ii) Each exterior angle = 2/5 of a right-angle
= 2/5 × 90˚
= 36˚
Let number of sides = n
∴ 360˚/n = 36˚
⇒ n = 360˚/36˚
⇒ n = 10
4. Is it possible to have a regular polygon whose each interior angle is :
(i) 170°
(ii) 138°
Solution
(i) No. of sides = n
each interior angle = 170°
∴ (n – 2)/n × 180˚ = 170˚
⇒ 180n - 360˚ = 170n
⇒ 180n – 170n = 360˚
⇒ 10n = 360˚
⇒ n = 360˚/10˚
⇒ n = 36
which is a whole number.
Hence it is possible to have a regular polygon whose interior angle is 170˚.
(ii) Let no. of sides = n
Each interior angle = 138˚
∴ (n – 2)/n × 180˚ = 138˚
⇒ 180n - 360˚ = 138n
⇒ 180n – 138n = 360˚
⇒ 42n = 360˚
⇒ n = 360˚/42
⇒ n = 60˚/7
Which is not a whole number.
Hence it is not possible to have a regular polygon having interior angle of 138°.
5. Is it possible to have a regular polygon whose each exterior angle is :
(i) 80°
(ii) 40% of a right angle.
Solution
(i) Let no. of sides = n each exterior angle = 80°
360˚/n = 80˚
⇒ n = 360˚/80˚
⇒ n = 9/2
Which is not a whole number.
Hence it is not possible to have a regular polygon whose each exterior angle is of 80°.
(ii) Let number of sides = n
Each exterior angle = 40% of a right angle
= 40/100 × 90
= 36˚
n = 360˚/36˚
⇒ n = 10
Which is a whole number.
Hence it is possible to have a regular polygon whose each exterior angle is 40% of a right angle.
6. Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
Solution
Let each exterior angle or interior angle be = x°
∴ x + x = 180˚
⇒ 2x = 180˚
⇒ x = 90˚
Now, let no. of sides = n
∵ Each exterior angle = 360˚/n
∴ 90˚ = 360˚/n
⇒ n = 360˚/90˚
⇒ n = 4
7. The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
Solution
Let interior angle = x°
Exterior angle = 1/3 x°
∴ x + 1/3x = 180˚
⇒ 3x + x = 540
⇒ 4x = 540
⇒ x = 540/4
⇒ x = 135˚
∴ Exterior angle = 1/3 × 135˚ = 45˚
Let no. of sides = n
∵ Each exterior angle = 360˚/n
∴ 45˚ = 360˚/n
∴ n = 360˚/45˚
⇒ n = 8
8. The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
Solution
Let exterior angle = x°
Interior angle = 5x°
x + 5x = 180°
⇒ 6x = 180°
⇒ x = 30°
Each exterior angle = 30°
Each interior angle = 5 x 30° = 150°
Let no. of sides = n
∵ each exterior angle = 360˚/n
30˚ = 360˚/n
⇒ n = 360˚/30˚
⇒ n = 12
Hence, (i) 150˚ (ii) 30˚ (iii) 12
9. The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon
Solution
Interior angle : exterior angle = 2 : 1
Let interior angle = 2x° & exterior angle = x°
∴ 2x˚ + x˚ = 180˚
⇒ 3x = 180˚
Let number of sides = n
∴ 360˚/n = 36˚
⇒ n = 360˚/36˚
⇒ n = 10
4. Is it possible to have a regular polygon whose each interior angle is :
(i) 170°
(ii) 138°
Solution
(i) No. of sides = n
each interior angle = 170°
∴ (n – 2)/n × 180˚ = 170˚
⇒ 180n - 360˚ = 170n
⇒ 180n – 170n = 360˚
⇒ 10n = 360˚
⇒ n = 360˚/10˚
⇒ n = 36
which is a whole number.
Hence it is possible to have a regular polygon whose interior angle is 170˚.
(ii) Let no. of sides = n
Each interior angle = 138˚
∴ (n – 2)/n × 180˚ = 138˚
⇒ 180n - 360˚ = 138n
⇒ 180n – 138n = 360˚
⇒ 42n = 360˚
⇒ n = 360˚/42
⇒ n = 60˚/7
Which is not a whole number.
Hence it is not possible to have a regular polygon having interior angle of 138°.
5. Is it possible to have a regular polygon whose each exterior angle is :
(i) 80°
(ii) 40% of a right angle.
Solution
(i) Let no. of sides = n each exterior angle = 80°
360˚/n = 80˚
⇒ n = 360˚/80˚
⇒ n = 9/2
Which is not a whole number.
Hence it is not possible to have a regular polygon whose each exterior angle is of 80°.
(ii) Let number of sides = n
Each exterior angle = 40% of a right angle
= 40/100 × 90
= 36˚
n = 360˚/36˚
⇒ n = 10
Which is a whole number.
Hence it is possible to have a regular polygon whose each exterior angle is 40% of a right angle.
6. Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
Solution
Let each exterior angle or interior angle be = x°
⇒ 2x = 180˚
⇒ x = 90˚
Now, let no. of sides = n
∵ Each exterior angle = 360˚/n
∴ 90˚ = 360˚/n
⇒ n = 360˚/90˚
⇒ n = 4
7. The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
Solution
Let interior angle = x°
Exterior angle = 1/3 x°
⇒ 3x + x = 540
⇒ 4x = 540
⇒ x = 540/4
⇒ x = 135˚
∴ Exterior angle = 1/3 × 135˚ = 45˚
Let no. of sides = n
∵ Each exterior angle = 360˚/n
∴ 45˚ = 360˚/n
∴ n = 360˚/45˚
⇒ n = 8
8. The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
Solution
Let exterior angle = x°
Interior angle = 5x°
x + 5x = 180°
⇒ 6x = 180°
⇒ x = 30°
Each exterior angle = 30°
Each interior angle = 5 x 30° = 150°
Let no. of sides = n
∵ each exterior angle = 360˚/n
30˚ = 360˚/n
⇒ n = 360˚/30˚
⇒ n = 12
Hence, (i) 150˚ (ii) 30˚ (iii) 12
9. The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon
Solution
Interior angle : exterior angle = 2 : 1
Let interior angle = 2x° & exterior angle = x°
⇒ 3x = 180˚
(i) x = 60˚
∴ Each exterior angle = 60˚
Let angle of sides = n
∴ 360˚/n = 60˚
⇒ n = 360˚/60˚
⇒ n = 360˚/60˚
(ii) n = 6
∴ (i) 60˚ (ii) 6
10. The ratio between the exterior angle and the interior angle of a regular polygon is 1: 4. Find the number of sides in the polygon.
Solution
Let exterior angle be x° & interior angle be 4x°
∴ 4x + x = 180˚
⇒ 5x = 180˚
⇒ x = 36˚
∴ Each exterior angle = 36˚
Let no. sides = n
∴ 360˚/n = 36˚
⇒ n = 360˚/36
⇒ n = 10
11. The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Solution
Let number of sides = n
Sum of exterior angles = 360°
Sum of interior angles = 360° × 2 = 720°
Sum of interior angles = (n – 2) × 180°
720° = (n – 2)× 180°
⇒ n – 2 = 720/180
⇒ n – 2 = 4
⇒ n = 4 + 2
⇒ n = 6
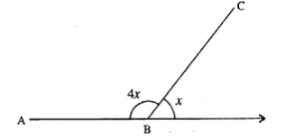
12. AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :
(i) its each interior angle,
(ii) its each exterior angle
(iii) the number of sides in the polygon.
Solution
∵ Polygon is regular (Given)
∴ AB = BC
⇒ ∠BAC = ∠BAC [∠s opp. to equal sides]
But ∠BAC = 20˚
∴ ∠BCA = 20˚
i.e., In ΔABC,
∠B + ∠BAC + ∠BCA = 180˚
⇒ ∠B + 20˚ + 20˚ = 180˚
⇒ ∠B = 180˚ - 40˚
⇒ ∠B = 140˚
(i) each interior angle = 140˚
(ii) each exterior angle = 180˚ - 140˚ = 40˚
(iii) Let no. of sides = n
∴ 360˚/n = 40˚
⇒ n = 360˚/40˚ = 9
⇒ n = 9
∴ (i) 140˚ (ii) 9
∴ Each exterior angle = 60˚
Let angle of sides = n
∴ 360˚/n = 60˚
⇒ n = 360˚/60˚
⇒ n = 360˚/60˚
(ii) n = 6
∴ (i) 60˚ (ii) 6
10. The ratio between the exterior angle and the interior angle of a regular polygon is 1: 4. Find the number of sides in the polygon.
Solution
Let exterior angle be x° & interior angle be 4x°
⇒ 5x = 180˚
⇒ x = 36˚
∴ Each exterior angle = 36˚
Let no. sides = n
∴ 360˚/n = 36˚
⇒ n = 360˚/36
⇒ n = 10
11. The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Solution
Let number of sides = n
Sum of exterior angles = 360°
Sum of interior angles = 360° × 2 = 720°
Sum of interior angles = (n – 2) × 180°
720° = (n – 2)× 180°
⇒ n – 2 = 720/180
⇒ n – 2 = 4
⇒ n = 4 + 2
⇒ n = 6
12. AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :
(i) its each interior angle,
(ii) its each exterior angle
(iii) the number of sides in the polygon.
Solution
∴ AB = BC
⇒ ∠BAC = ∠BAC [∠s opp. to equal sides]
But ∠BAC = 20˚
∴ ∠BCA = 20˚
i.e., In ΔABC,
∠B + ∠BAC + ∠BCA = 180˚
⇒ ∠B + 20˚ + 20˚ = 180˚
⇒ ∠B = 180˚ - 40˚
⇒ ∠B = 140˚
(i) each interior angle = 140˚
(ii) each exterior angle = 180˚ - 140˚ = 40˚
(iii) Let no. of sides = n
∴ 360˚/n = 40˚
⇒ n = 360˚/40˚ = 9
⇒ n = 9
∴ (i) 140˚ (ii) 9
13. Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.
Solution
Let number of sides of regular polygon = n
AB & DC when produced meet at P such that
∠P = 90˚
∵ Interior angles are equal.
∴ ∠ABC = ∠BCD
∴ 180˚ - ∠ABC = 180˚ - ∠BCD
∴ ∠PBC = ∠BCP
But ∠P = 90˚ (Given)
∴ ∠PBC + ∠BCP = 180˚ - 90˚ = 90˚
∴ ∠PBC = ∠BCP
= ½ × 90˚
= 45˚
∴ Each exterior angle = 45˚
∴ 45˚ = 360˚/n
⇒ n = 360˚/45˚
⇒ n = 8
14. In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Solution
(i) Since number of sides in the pentagon = 5
Each exterior angle = 360/5 = 72°
∠BAE = 180° – 72°= 108°
(ii) In ΔABE, AB = AE
∴ ∠ABE = ∠AEB
But ∠BAE + ∠ABE + ∠AEB = 180˚
∴ 108˚ + 2∠ABE
= 180˚ - 108˚
= 72˚
⇒ ∠ABE = 36˚
(iii) Since ∠AED = 108˚
[∵ each interior angle = 108˚]
⇒ ∠AEB = 36˚
⇒ ∠BED = 108˚ - 36˚
= 72˚
15. The difference between the exterior angles of two regular polygons, having the sides equal to (n – 1) and (n + 1) is 9°. Find the value of n.
Solution
We know that sum of exterior angles of a polynomial is 360°
Solution
AB & DC when produced meet at P such that
∠P = 90˚
∵ Interior angles are equal.
∴ ∠ABC = ∠BCD
∴ 180˚ - ∠ABC = 180˚ - ∠BCD
∴ ∠PBC = ∠BCP
But ∠P = 90˚ (Given)
∴ ∠PBC + ∠BCP = 180˚ - 90˚ = 90˚
∴ ∠PBC = ∠BCP
= ½ × 90˚
= 45˚
∴ Each exterior angle = 45˚
∴ 45˚ = 360˚/n
⇒ n = 360˚/45˚
⇒ n = 8
14. In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Solution
(i) Since number of sides in the pentagon = 5
Each exterior angle = 360/5 = 72°
∠BAE = 180° – 72°= 108°
∴ ∠ABE = ∠AEB
But ∠BAE + ∠ABE + ∠AEB = 180˚
∴ 108˚ + 2∠ABE
= 180˚ - 108˚
= 72˚
⇒ ∠ABE = 36˚
(iii) Since ∠AED = 108˚
[∵ each interior angle = 108˚]
⇒ ∠AEB = 36˚
⇒ ∠BED = 108˚ - 36˚
= 72˚
15. The difference between the exterior angles of two regular polygons, having the sides equal to (n – 1) and (n + 1) is 9°. Find the value of n.
Solution
We know that sum of exterior angles of a polynomial is 360°
(i) If sides of a regular polygon = n – 1
Then each angle = 360˚/(n – 1)
And if sides are n + 1, then each angle = 360˚/(n +1)
According to the condition,
360˚/(n – 1) - 360˚/(n + 1) = 9
⇒ 360˚[1/(x - 1) - 1/(x + 1)] = 9
⇒ 360˚ [(n + 1 – n + 1)/(n – 1)(n + 1)] = 9
⇒ (2 × 360)/(n2 – 1) = 9
⇒ n2 – 1 = (2×360)/9 = 80
⇒ n2 – 1 = 80
⇒ n2 = 1 – 80 = 0
⇒ n2 – 81 = 0
⇒ (n)2 – (9)2 = 0
⇒ (n + 9)(n – 9) = 0
Either n + 9 = 0, then n = -9 which is not possible being negative,
Or, n – 9 = 0, then n = 9
∴ n = 9
∴ No. of sides of a regular polygon = 9
16. If the difference between the exterior angle of a n sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.
Solution
We know that sum of exterior angles of a polygon = 360°
Each exterior angle of a regular polygon of 360°
sides = 360˚/n
And exterior angle of the regular polygon of (n + 1) sides = 360˚/(n + 1)
∴ 360˚/n - 360˚/(n + 1) = 12
⇒ 360 [1/n – 1/(n + 1)] = 12
⇒ 360[(n + 1 – n)/n(n + 1)] = 12
⇒ (30 × 1)/(n2 + n) = 12
⇒ 12(n2 + n) = 360˚
⇒ n2 + n = 36˚ (Dividing by 12)
⇒ n2 + n – 30 = 0
⇒ n2 + 6n – 5n – 30 = 0 {∵ -30 = 6 ×(-5) = 1= 6 – 5}
⇒ n(n + 6) – 5(n + 6) = 0
⇒ (n + 6)(n – 5) = 0
Either n + 6 = 0, then n = - 6 which is not possible being negative
Or, n – 5 = 0, then n = 5
Hence, n = 5
17. The ratio between the number of sides of two regular polygons is 3:4 and the ratio between the sum of their interior angles is 2:3. Find the number of sides in each polygon.
Solution
Ratio of sides of two regular polygons = 3 : 4
Let sides of first polygon = 3n
and sides of second polygon = 4n
Sum of interior angles of first polygon = (2 × 3n – 4) × 90 ˚
= (6n – 4) × 90˚ and sum of interior angle of second polygon = (2 × 4n – 4) × 90˚
= (8n – 4) × 90˚
∴ ((6n – 4) × 90˚)/((8n – 4) × 90˚) = 2/3
⇒ (6n – 4)/(8n – 4) = 2/3
⇒ 18n – 12 = 16n – 8
⇒ 18n – 16n = -8 + 12
⇒ 2n = 4
⇒ n = 2
∴ No. of sides of first polygon = 3n = 3 × 2 = 6
And no. of sides of second polygon = 4n
= 4 × 2
= 8
18. Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.
Solution
Sum of exterior angles of a hexagon = 4 x 90° = 360°
Three angles are 40°, 51° and 86°
Sum of three angle = 40° + 51° + 86° = 177°
Sum of other three angles = 360° – 177° = 183°
Each angle is x°
3x = 183°
⇒ x = 183/3
Hence x = 61
19. Calculate the number of sides of a regular polygon, if:
(i) its interior angle is five times its exterior angle.
(ii) the ratio between its exterior angle and interior angle is 2:7.
(iii) its exterior angle exceeds its interior angle by 60°.
Solution
Let number of sides of a regular polygon = n
(i) Let exterior angle = x
Then interior angle = 5x
x + 5x = 180°
⇒ 6x = 180°
⇒ x = 180˚/6 = 30˚
∴ Number of sides(n) = 360˚/30 = 12
(ii) Ratio between exterior angle and interior angle = 2 : 7
Let exterior angle = 2x
Then interior angle = 7x
∴ 2x + 7x = 180˚
⇒ 9x = 180˚
⇒ x = 180˚/9
= 20˚
∴ Ext. angle = 2x = 2 × 20˚ = 40˚
∴ No. of sides = 360˚/40 = 9
(iii) Let interior angle = x
Then exterior angle = x + 60
∴ x + x + 60˚ = 180˚
⇒ 2x = 180˚ - 60˚ = 120˚
⇒ x = 120˚/2 = 60˚
∴ Exterior angle = 60˚ + 60˚ = 120˚
∴ Number of sides = 360˚/120˚ = 3
20. The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Solution
Sum of interior angles = 3 x Sum of exterior angles
Let exterior angle = x
The interior angle = 3x
x + 3x=180°
⇒ 4x = 180°
⇒ x = 180˚/4
⇒ x = 45°
Number of sides = 360/45 = 8
Then each angle = 360˚/(n – 1)
And if sides are n + 1, then each angle = 360˚/(n +1)
According to the condition,
360˚/(n – 1) - 360˚/(n + 1) = 9
⇒ 360˚[1/(x - 1) - 1/(x + 1)] = 9
⇒ 360˚ [(n + 1 – n + 1)/(n – 1)(n + 1)] = 9
⇒ (2 × 360)/(n2 – 1) = 9
⇒ n2 – 1 = (2×360)/9 = 80
⇒ n2 – 1 = 80
⇒ n2 = 1 – 80 = 0
⇒ n2 – 81 = 0
⇒ (n)2 – (9)2 = 0
⇒ (n + 9)(n – 9) = 0
Either n + 9 = 0, then n = -9 which is not possible being negative,
Or, n – 9 = 0, then n = 9
∴ n = 9
∴ No. of sides of a regular polygon = 9
16. If the difference between the exterior angle of a n sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.
Solution
We know that sum of exterior angles of a polygon = 360°
Each exterior angle of a regular polygon of 360°
sides = 360˚/n
And exterior angle of the regular polygon of (n + 1) sides = 360˚/(n + 1)
∴ 360˚/n - 360˚/(n + 1) = 12
⇒ 360 [1/n – 1/(n + 1)] = 12
⇒ 360[(n + 1 – n)/n(n + 1)] = 12
⇒ (30 × 1)/(n2 + n) = 12
⇒ 12(n2 + n) = 360˚
⇒ n2 + n = 36˚ (Dividing by 12)
⇒ n2 + n – 30 = 0
⇒ n2 + 6n – 5n – 30 = 0 {∵ -30 = 6 ×(-5) = 1= 6 – 5}
⇒ n(n + 6) – 5(n + 6) = 0
⇒ (n + 6)(n – 5) = 0
Either n + 6 = 0, then n = - 6 which is not possible being negative
Or, n – 5 = 0, then n = 5
Hence, n = 5
17. The ratio between the number of sides of two regular polygons is 3:4 and the ratio between the sum of their interior angles is 2:3. Find the number of sides in each polygon.
Solution
Ratio of sides of two regular polygons = 3 : 4
Let sides of first polygon = 3n
and sides of second polygon = 4n
Sum of interior angles of first polygon = (2 × 3n – 4) × 90 ˚
= (6n – 4) × 90˚ and sum of interior angle of second polygon = (2 × 4n – 4) × 90˚
= (8n – 4) × 90˚
∴ ((6n – 4) × 90˚)/((8n – 4) × 90˚) = 2/3
⇒ (6n – 4)/(8n – 4) = 2/3
⇒ 18n – 12 = 16n – 8
⇒ 18n – 16n = -8 + 12
⇒ 2n = 4
⇒ n = 2
∴ No. of sides of first polygon = 3n = 3 × 2 = 6
And no. of sides of second polygon = 4n
= 4 × 2
= 8
18. Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.
Solution
Sum of exterior angles of a hexagon = 4 x 90° = 360°
Three angles are 40°, 51° and 86°
Sum of three angle = 40° + 51° + 86° = 177°
Sum of other three angles = 360° – 177° = 183°
Each angle is x°
3x = 183°
⇒ x = 183/3
Hence x = 61
19. Calculate the number of sides of a regular polygon, if:
(i) its interior angle is five times its exterior angle.
(ii) the ratio between its exterior angle and interior angle is 2:7.
(iii) its exterior angle exceeds its interior angle by 60°.
Solution
Let number of sides of a regular polygon = n
(i) Let exterior angle = x
Then interior angle = 5x
x + 5x = 180°
⇒ 6x = 180°
⇒ x = 180˚/6 = 30˚
∴ Number of sides(n) = 360˚/30 = 12
(ii) Ratio between exterior angle and interior angle = 2 : 7
Let exterior angle = 2x
Then interior angle = 7x
∴ 2x + 7x = 180˚
⇒ 9x = 180˚
⇒ x = 180˚/9
= 20˚
∴ Ext. angle = 2x = 2 × 20˚ = 40˚
∴ No. of sides = 360˚/40 = 9
(iii) Let interior angle = x
Then exterior angle = x + 60
∴ x + x + 60˚ = 180˚
⇒ 2x = 180˚ - 60˚ = 120˚
⇒ x = 120˚/2 = 60˚
∴ Exterior angle = 60˚ + 60˚ = 120˚
∴ Number of sides = 360˚/120˚ = 3
20. The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Solution
Sum of interior angles = 3 x Sum of exterior angles
Let exterior angle = x
The interior angle = 3x
x + 3x=180°
⇒ 4x = 180°
⇒ x = 180˚/4
⇒ x = 45°
Number of sides = 360/45 = 8
Exercise 16 C
1. Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Solution
Let the other angle = x°
According to given,
89° + 113° + x° + x° = 360°
⇒ 2x° = 360° – 202°
⇒ 2x° = 158°
⇒ x° = 158/2
other two angles = 79° each
2. Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5:7; find the measure of each of them.
Solution
Two angles are 68° and 76°
Let other two angles be 5x and 7x
68° + 76°+ 5x + 7x = 360°
⇒ 12x + 144° = 360°
⇒ 12x = 360° – 144°
⇒ 12x = 216°
⇒ x = 18°
angles are 5x and 7x
i.e. 5×18° and 7×18° i.e. 90° and 126°
3. Angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x – 20)° and 6(x + 3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Solution
Angles of quadrilateral are,
(4x)˚, 5(x + 2)˚, (7x – 20)˚ and 6(x + 3)˚
∴ 4x + 5(x + 2) + (7x – 20)+ 6(x + 3) = 360˚
⇒ 4x + 5x + 10 + 7x – 20 + 6x + 18 = 360˚
⇒ 22x + 8 = 360˚
⇒ 22x = 360˚ - 8˚
⇒ 22x = 352˚
⇒ x = 16˚
Hence angle are,
(4x)˚ = (4 × 16)˚ = 64˚
5(x + 2)˚ = 5(16 + 2)˚ = 90˚
(7x – 20)˚ = (7 × 16 – 20)˚ = 92˚
6(x + 3)˚ = 6(16 + 3) = 114˚
4. Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
Solution
∵ ∠A = 90˚ (Given)
∠B = (2x + 4˚)
∠C = (3x - 5˚)
∠D = (8x - 15˚)
∠A + ∠B + ∠C + ∠D = 360˚
90˚ + (2x + 4) + (3x – 5) + (8x – 15) = 360
⇒ 90 + 2x + 4 + 3x – 5 + 8x – 15 = 360
⇒ 74˚ + 13x = 360˚
⇒ 13x = 360˚ - 74˚
⇒ 13x = 286˚
⇒ x = 22˚
∵ ∠B = 2x + 4 = 2×22˚ + 4 = 48˚
∠C = 3x – 5 = 3 × 22˚ - 5 = 61˚
Hence (i)22˚ (ii) ∠B = 48˚, ∠C = 61˚
5. In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
Solution
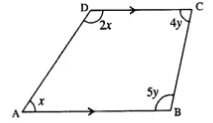∵ ∠A : ∠D = 1 : 2
Let ∠A = x and ∠B = 2x
∵ ∠C : ∠B = 4 : 5
Let ∠C = 4y and ∠B = 5y
∵ AB ∥ DC
∴ ∠A + ∠D = 180˚
x + 2x = 180˚
⇒ 3x = 180˚
⇒ x = 60˚
∴ A = 60˚
∠D = 2x = 2 × 60˚ = 120˚
Again ∠B + ∠C = 180˚
5y + 4y = 180˚
⇒ 9y = 180˚
⇒ y = 20˚
∴ ∠B = 5y = 5 × 20˚ = 100˚
∠C = 4y = 4 × 20˚ = 80˚
Hence ∠A = 60˚ : ∠B = 100˚ : ∠C = 80˚ ∠D = 120˚
(iii) Quadrilateral ABCD is a trapezium because one pair of opposite side is parallel.
6. From the following figure find ;
(i) x
(ii) ∠ABC
(iii) ∠ACD
Solution
(i) In Quadrilateral ABCD,
x + 4x + 3x + 4x + 48° = 360°
⇒ 12x = 360° – 48°
⇒ 12x = 312
⇒ x = 312/12 = 26˚
Solution
Let the other angle = x°
According to given,
89° + 113° + x° + x° = 360°
⇒ 2x° = 360° – 202°
⇒ 2x° = 158°
⇒ x° = 158/2
other two angles = 79° each
2. Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5:7; find the measure of each of them.
Solution
Two angles are 68° and 76°
Let other two angles be 5x and 7x
68° + 76°+ 5x + 7x = 360°
⇒ 12x + 144° = 360°
⇒ 12x = 360° – 144°
⇒ 12x = 216°
⇒ x = 18°
angles are 5x and 7x
i.e. 5×18° and 7×18° i.e. 90° and 126°
3. Angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x – 20)° and 6(x + 3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Solution
Angles of quadrilateral are,
(4x)˚, 5(x + 2)˚, (7x – 20)˚ and 6(x + 3)˚
∴ 4x + 5(x + 2) + (7x – 20)+ 6(x + 3) = 360˚
⇒ 4x + 5x + 10 + 7x – 20 + 6x + 18 = 360˚
⇒ 22x + 8 = 360˚
⇒ 22x = 360˚ - 8˚
⇒ 22x = 352˚
⇒ x = 16˚
Hence angle are,
(4x)˚ = (4 × 16)˚ = 64˚
5(x + 2)˚ = 5(16 + 2)˚ = 90˚
(7x – 20)˚ = (7 × 16 – 20)˚ = 92˚
6(x + 3)˚ = 6(16 + 3) = 114˚
4. Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
∵ ∠A = 90˚ (Given)
∠B = (2x + 4˚)
∠C = (3x - 5˚)
∠D = (8x - 15˚)
∠A + ∠B + ∠C + ∠D = 360˚
90˚ + (2x + 4) + (3x – 5) + (8x – 15) = 360
⇒ 90 + 2x + 4 + 3x – 5 + 8x – 15 = 360
⇒ 74˚ + 13x = 360˚
⇒ 13x = 360˚ - 74˚
⇒ 13x = 286˚
⇒ x = 22˚
∵ ∠B = 2x + 4 = 2×22˚ + 4 = 48˚
∠C = 3x – 5 = 3 × 22˚ - 5 = 61˚
Hence (i)22˚ (ii) ∠B = 48˚, ∠C = 61˚
5. In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
Solution
Let ∠A = x and ∠B = 2x
∵ ∠C : ∠B = 4 : 5
Let ∠C = 4y and ∠B = 5y
∵ AB ∥ DC
∴ ∠A + ∠D = 180˚
x + 2x = 180˚
⇒ 3x = 180˚
⇒ x = 60˚
∴ A = 60˚
∠D = 2x = 2 × 60˚ = 120˚
Again ∠B + ∠C = 180˚
5y + 4y = 180˚
⇒ 9y = 180˚
⇒ y = 20˚
∴ ∠B = 5y = 5 × 20˚ = 100˚
∠C = 4y = 4 × 20˚ = 80˚
Hence ∠A = 60˚ : ∠B = 100˚ : ∠C = 80˚ ∠D = 120˚
(iii) Quadrilateral ABCD is a trapezium because one pair of opposite side is parallel.
6. From the following figure find ;
(i) x
(ii) ∠ABC
(iii) ∠ACD
Solution
(i) In Quadrilateral ABCD,
x + 4x + 3x + 4x + 48° = 360°
⇒ 12x = 360° – 48°
⇒ 12x = 312
⇒ x = 312/12 = 26˚
(ii) ∠ABC = 4x
4 × 26 = 104˚
(iii) ∠ACD = 180˚ - 4x - 48˚
= 180˚ - 4×26 - 48 ˚
= 180˚ - 104˚ - 48˚
= 180˚ - 152˚
= 28˚
7. Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a + 2)° and ∠B = 2(2a + 7)°.
Calculate ∠A.
Solution 7:
∠C = 64° (Given)
∠D = ∠C – 8° = 64° - 8° = 56°
∠A = 5(a + 2)°
∠B = 2(2a + 7)°
Now, ∠A + ∠B + ∠C + ∠D = 360°
5(a + 2)° + 2(2a + 7)° + 64° + 56° = 360°
⇒ 5a + 10 + 4a + 14° + 64° + 56° = 360°
⇒ 9a + 144° = 360°
⇒ 9a = 360° – 144°
⇒ 9a = 216°
⇒ a = 24°
∠A = 5 (a + 2) = 5(24 + 2) = 130°
8. In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
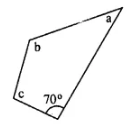Solution
Stun of angles of quadrilateral = 360°
70° + a + 2a + 15 + 3a + 5 = 360°
⇒ 6a + 90° = 360°
⇒ 6a = 270°
⇒ a = 45°
b = 2a + 15 = 2×45 + 15 = 105°
c = 3a + 5 = 3×45 + 5 = 140°
Hence ∠b and ∠c are 105° and 140°
9. Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
Solution
Let each equal angle be x°
x + x + x + 69° = 360°
3x = 360° - 69
⇒ 3x = 291
⇒ x = 97°
Each, equal angle = 97°
10. In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
Solution
∵ ∠P : ∠Q + ∠R : ∠S = 3 : 4 : 5 : 6
Let ∠P = 3x
∠Q = 4x
∠R = 6x
∠S = 7x
∴ ∠P + ∠Q + ∠R + ∠S = 360˚
⇒ 3x + 4x + 6x + 7x = 360˚
⇒ 20x = 360˚
⇒ x = 18˚
∴ ∠P = 3x = 3 × 18 = 54˚
∠Q = 4x = 4 × 18 = 72˚
∠R = 6x = 6 × 18 = 108˚
∠S = 7x = 7 × 18 = 126˚
∠Q + ∠R = 72˚ + 108˚ = 180˚
Or ∠P + ∠S = 54˚ + 126 ˚ = 180˚
Hence PQ ∥ SR
As ∠P + ∠Q = 72˚ + 54˚ = 126˚
Which is ≠ 180˚
∴ PS and QR are not parallel.
4 × 26 = 104˚
(iii) ∠ACD = 180˚ - 4x - 48˚
= 180˚ - 4×26 - 48 ˚
= 180˚ - 104˚ - 48˚
= 180˚ - 152˚
= 28˚
7. Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a + 2)° and ∠B = 2(2a + 7)°.
Calculate ∠A.
Solution 7:
∠C = 64° (Given)
∠D = ∠C – 8° = 64° - 8° = 56°
∠A = 5(a + 2)°
∠B = 2(2a + 7)°
Now, ∠A + ∠B + ∠C + ∠D = 360°
5(a + 2)° + 2(2a + 7)° + 64° + 56° = 360°
⇒ 5a + 10 + 4a + 14° + 64° + 56° = 360°
⇒ 9a + 144° = 360°
⇒ 9a = 360° – 144°
⇒ 9a = 216°
⇒ a = 24°
∠A = 5 (a + 2) = 5(24 + 2) = 130°
8. In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.
Stun of angles of quadrilateral = 360°
70° + a + 2a + 15 + 3a + 5 = 360°
⇒ 6a + 90° = 360°
⇒ 6a = 270°
⇒ a = 45°
b = 2a + 15 = 2×45 + 15 = 105°
c = 3a + 5 = 3×45 + 5 = 140°
Hence ∠b and ∠c are 105° and 140°
9. Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
Solution
Let each equal angle be x°
x + x + x + 69° = 360°
⇒ 3x = 291
⇒ x = 97°
Each, equal angle = 97°
10. In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
Solution
∵ ∠P : ∠Q + ∠R : ∠S = 3 : 4 : 5 : 6
Let ∠P = 3x
∠Q = 4x
∠R = 6x
∠S = 7x
∴ ∠P + ∠Q + ∠R + ∠S = 360˚
⇒ 3x + 4x + 6x + 7x = 360˚
⇒ 20x = 360˚
⇒ x = 18˚
∴ ∠P = 3x = 3 × 18 = 54˚
∠Q = 4x = 4 × 18 = 72˚
∠R = 6x = 6 × 18 = 108˚
∠S = 7x = 7 × 18 = 126˚
∠Q + ∠R = 72˚ + 108˚ = 180˚
Or ∠P + ∠S = 54˚ + 126 ˚ = 180˚
Hence PQ ∥ SR
As ∠P + ∠Q = 72˚ + 54˚ = 126˚
Which is ≠ 180˚
∴ PS and QR are not parallel.
(ii) PQRS is a trapezium as its one pair of opposite side is parallel.
11. Use the information given in the following figure to find the value of x.
Solution
Take A, B, C, D as the vertices of Quadrilateral and BA is produced to E (say).
Since ∠EAD = 70°
∠DAB = 180° – 70° = 110°
[EAB is a straight line and AD stands on it ∠EAD + ∠DAB = 180°]
110° + 80° + 56° + 3x – 6° = 360°
[sum of interior angles of a quadrilateral = 360°]
3x = 360° – 110° – 80° – 56° + 6°
⇒ 3x = 360° – 240° = 120°
⇒ x = 40°
12. The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
Solution
Let ∠A = 4x
∠D = 5x
Since ∠A + ∠D = 180° [AB || DC]
4x + 5x = 180°
⇒ 9x = 180°
⇒ x = 20°
∠A = 4 (20) = 80°,
∠D = 5 (20) = 100°
Again ∠B + ∠C = 180° [ AB || DC]
3x – 15° + 4x + 20° = 180°
⇒ 7x = 180° – 5°
⇒ 7x = 175°
⇒ x = 25°
∠B = 75° – 15° = 60°
and ∠C = 4(25) + 20 = 100° + 20° = 120°
13. Use the following figure to find the value of x
Solution
The sum of exterior angles of a quadrilateral
y + 80° + 60° + 90° = 360°
⇒ y + 230° = 360°
⇒ y = 360° – 230° = 130°
At vertex A,
∠y + ∠x = 180° (Linear pair)
x = 180° – 130°
⇒ x = 50°
14. ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Solution
Given: ABCDE is a regular pentagon.
The bisector ∠A of the pentagon meets the side CD at point M.
To prove: ∠AMC = 90°
Proof:
11. Use the information given in the following figure to find the value of x.
Take A, B, C, D as the vertices of Quadrilateral and BA is produced to E (say).
Since ∠EAD = 70°
∠DAB = 180° – 70° = 110°
[EAB is a straight line and AD stands on it ∠EAD + ∠DAB = 180°]
110° + 80° + 56° + 3x – 6° = 360°
[sum of interior angles of a quadrilateral = 360°]
3x = 360° – 110° – 80° – 56° + 6°
⇒ 3x = 360° – 240° = 120°
⇒ x = 40°
12. The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
Let ∠A = 4x
∠D = 5x
Since ∠A + ∠D = 180° [AB || DC]
4x + 5x = 180°
⇒ 9x = 180°
⇒ x = 20°
∠A = 4 (20) = 80°,
∠D = 5 (20) = 100°
Again ∠B + ∠C = 180° [ AB || DC]
3x – 15° + 4x + 20° = 180°
⇒ 7x = 180° – 5°
⇒ 7x = 175°
⇒ x = 25°
∠B = 75° – 15° = 60°
and ∠C = 4(25) + 20 = 100° + 20° = 120°
13. Use the following figure to find the value of x
The sum of exterior angles of a quadrilateral
⇒ y + 230° = 360°
⇒ y = 360° – 230° = 130°
At vertex A,
∠y + ∠x = 180° (Linear pair)
x = 180° – 130°
⇒ x = 50°
14. ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Solution
The bisector ∠A of the pentagon meets the side CD at point M.
To prove: ∠AMC = 90°
Proof:
We know that, the measure of each interior angle of a regular pentagon is 108°.
∠BAM = 1/2 x 108° = 54°
Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
⇒ 54° + 108° + 108° + ∠AMC = 360°
⇒ ∠AMC = 360° – 270°
⇒ ∠AMC = 90°
15. In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = 1/2 (∠C + ∠D)
Solution
Given: AO and BO are the bisectors of ∠A and ∠B respectively.
∠1 = ∠4 and ∠3 = ∠5 ...(i)
To prove: ∠AOB = 1/2 (∠C + ∠D)
Proof:
∠BAM = 1/2 x 108° = 54°
Since, we know that the sum of a quadrilateral is 360°
In quadrilateral ABCM, we have
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
⇒ 54° + 108° + 108° + ∠AMC = 360°
⇒ ∠AMC = 360° – 270°
⇒ ∠AMC = 90°
15. In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = 1/2 (∠C + ∠D)
Solution
Given: AO and BO are the bisectors of ∠A and ∠B respectively.
∠1 = ∠4 and ∠3 = ∠5 ...(i)
Proof:
In quadrilateral ABCD
∠A + ∠B + ∠C + ∠D = 360°
1/2 (∠A + ∠B + ∠C + ∠D) = 180° …(ii)
Now in ∆AOB
∠1 + ∠2 + ∠3 = 180° …(iii)
Equating equation (ii) and equation (iii), we get
∠1 + ∠2 + ∠3 = ∠A + ∠B + 1/2 (∠C + ∠D)
⇒ ∠1 + ∠2 + ∠3 = ∠1 + ∠3 + 1/2 (∠C + ∠D)
⇒ ∠2 = 1/2 (∠C + ∠D)
⇒ ∠AOB = 1/2 (∠C + ∠D)
Hence proved.
∠A + ∠B + ∠C + ∠D = 360°
1/2 (∠A + ∠B + ∠C + ∠D) = 180° …(ii)
Now in ∆AOB
∠1 + ∠2 + ∠3 = 180° …(iii)
Equating equation (ii) and equation (iii), we get
∠1 + ∠2 + ∠3 = ∠A + ∠B + 1/2 (∠C + ∠D)
⇒ ∠1 + ∠2 + ∠3 = ∠1 + ∠3 + 1/2 (∠C + ∠D)
⇒ ∠2 = 1/2 (∠C + ∠D)
⇒ ∠AOB = 1/2 (∠C + ∠D)
Hence proved.