Chapter 15 Circle ML Aggarwal ICSE Solutions for Class 9 Maths

ML Aggarwal Solutions for Chapter 15 Circle Class 9 Maths ICSE

Here, we are providing the solutions for Chapter 15 Circle from ML Aggarwal Textbook for Class 9 ICSE Mathematics. Solutions of the fourteen chapter has been provided in detail. This will help the students in understanding the chapter more clearly. Class 9 Chapter 15 Circle ML Aggarwal Solutions for ICSE is one of the most important chapter for the board exams which is based on calculating length of chord, distance from the centre of the circle, radius of the circle, circle inscribed in a triangle and finding bisector of the arc.

Exercise 15.1

1. Calculate the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13 cm.

Solution

AB is chord of a circle with center O and OA is its radius OM ⊥ AB

Therefore, OA = 13 cm, OM = 12 cm

Now from right angled triangle OAM,

OA² = OM² + AM² by using Pythagoras theorem,

⇒ 13² = 12² + AM²

⇒ AM² = 13² – 12²

⇒ AM² = 169 – 144

⇒ AM² = 25

⇒ AM² = 5²

⇒ AM = 5

We know that OM perpendicular to AB

Therefore, M is the midpoint of AB

AB = 2 AM

⇒ AB = 2 (5)

⇒ AB = 10 cm

2. A chord of length 48 cm is drawn in a circle of radius 25 cm. Calculate its distance from the center of the circle.

Solution

AB is the chord of the circle with centre O and radius OA

OM is perpendicular to AB

Therefore, AB = 48 cm

OA = 25 cm

OM ⊥ AB

M is the mid-point of AB

AM = 1/2 AB = ½ × 48 = 24 cm

Now right ∆OAM,

OA² = OM² + AM² (by Pythagoras Axiom)

⇒ (25)² = OM ² + (24)²

⇒ OM² = (25)² – (24)² = 625 – 576

⇒ OM² = 49 = (7)²

⇒ OM = 7 cm

3. A chord of length 8 cm is at a distance of 3 cm from the centre of the circle. Calculate the radius of the circle.

Solution

AB is the chord of a circle with center O

And radius OA and OM ⊥ AB

AB = 8 cm

OM = 3 cm

OM ⊥ AB

M is the mid-point of AB

AM = ½ AB = ½ × 8 = 4 cm.

Now in right ∆OAM

OA² = OM² + AM² (By Pythagoras Axiom)

= (3)² + (4)² = 9 + 16 = 25

= (5)²

⇒ OA = 5 cm.

4. Calculate the length of the chord which is at a distance of 6 cm from the centre of a circle of diameter 20 cm.

Solution

AB is the chord of the circle with centre O

And radius OA and OM ⊥ AB

Diameter of the circle = 20 cm

Radius = 20/2 = 10 cm

OA = 10 cm, OM = 6 cm

Now in right ∆OAM,

OA² = AM² + OM² (By Pythagoras Axiom)

⇒ (10)² = AM² + (6)²

⇒ AM² = 10² – 6²

⇒ AM² = 100 – 36 = 64 = (8)²

⇒ AM = 8 cm

OM ⊥ AB

M is the mid-point of AB.

⇒ AB = 2× AM = 2×8 = 16 cm.

5. A chord of length 16 cm is at a distance of 6 cm from the centre of the circle. Find the length of the chord of the same circle which is at a distance of 8 cm from the centre.

Solution

AB is a chord a circle with centre O and

OA is the radius of the circle and OM ⊥ AB

AB = 16 cm, OM = 6 cm

OM ⊥ AB

AM = ½ AB = ½ × 16 = 8 cm

Now in right ∆OAM

OA² = AM² + OM² (By Pythagoras Axiom)

= (8)² + (6)²

⇒ 64 + 36 = 100 = (10)²

Now CD is another chord of the same circle

ON ⊥ CD and OC is the radius.

In right ∆ONC

OC² = ON² + NC² (By Pythagoras Axioms)

⇒ (10)² = (8)² + (NC)²

⇒ 100 = 64 + NC²

⇒ NC ² = 100 – 64 = 36 = (6)²

⇒ NC = 6

But ON ⊥ AB

N is the mid-point of CD

⇒ CD = 2 NC = 2×6 = 12 cm

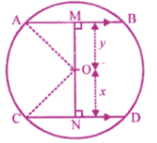
6. In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on :

(i) the same side of the centre.

(ii) the opposite sides of the centre

Solution

Two chords AB and CD of a Circle with centre O and radius OA or OC

OA = OC = 5 cm

AB = 8 cm

CD = 6 cm

OM and ON are perpendiculars from O to AB and CD respectively.

M and N are the Mid-points of AB and

CD respectively

In figure (i) chord are on the same side

And in figure (ii) chord are on the opposite

Sides of the centre

In right ∆OAM

OA² = AM² + OM² (By Pythagoras Axiom)

⇒ (5)² = (4)² + OM²

⇒ AM = ½ AB

⇒ 25 = 16 + OM²

⇒ OM² = 25 – 16 = 9= (3)²

⇒ OM = 3 cm

Again in right ∆OCN,

OC² = CN² + ON²

⇒ (5)² = (3)² + ON²

⇒ (CN = ½ CD)

⇒ 25 = 9 + ON²

⇒ ON² = 25 – 9 = 16 = (4)²

⇒ ON = 4

In fig (i), distance MN = ON – OM

= 4 – 3 = 1cm.

In fig (ii)

MN = OM + ON = 3 + 4 = 7 Cm

7. (a) In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle, OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the:

(i) radius of the circle.

(ii) length of chord CD.

(b) In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.

Solution

(a)Given : AB = 24 cm, OM = 5cm, ON = 12cm

OM ⊥ AB

M is midpoint of AB

AM = 12 cm

(i) Radius of circle OA = √OM² + AM²

(ii) Again OC² = ON² + CN²

⇒ 13² = 12² + CN²

⇒ CN = √(13² – 12²) = √(169 – 144) = √25

⇒ CN = 5 cm

As ON ⊥ CD, N is mid-Point of CD

CD = 2CN = 2×5 = 10 cm

(b) AB = 8 cm, EC = 3 cm

Let radius OB = OC = r

OE = (r-3) cm

Now in right ∆OBE

OB² = BE² + OE²

⇒ r² = (4)² + (r – 3)²

⇒ r² = 16 + r² – 6r + 9

⇒ 6r = 25

⇒ r = 25/6 = 4 1/6 cm

8. In the adjoining figure, AB and CD ate two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.

Solution

In the figure, chords AB ∥ CD

O is the centre of the circle

Radius of the Circle = 15 cm

Length of AB = 24 cm and CD = 18 cm

Join OA and OC

AB = 24 cm and OM ⊥ AB

AM = MB = 24/2 = 12 cm

Similarly ON ⊥ CD

CN = ND = 18/2 = 9 cm

Similarly In right ∆ CNO

OC² = CN² + ON² (15)² = (9)² + ON²

⇒ 225 = 81 + ON²

⇒ ON² = 225 – 81 = 144 = (12)²

⇒ ON = 12 cm

Now MN = OM + ON = 9 + 12 = 21 cm

9. AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.

Solution 

AB and CD are two parallel chords and AB = 10 cm, CD = 4 cm and distance between

AB and CD = 3 cm

Let radius of circle OA = OC = r

OM ⊥ CD which intersects AB in L.

Let OL =x, then OM = x + 3

Now right ∆OLA

OA² = AL² + OL²

⇒ r² = (5)² + x² = 25 + x² (l is mid- point of AB)

Again in right ∆OCM

OC² = CM² + OM²

⇒ r² = (2)² + (x + 3)² (M is mid-point of CD)

⇒ r² = 4 + (x + 3)² (M is mid-Point of CD)

⇒ r² = 4 + (x + 3)²

from (i) and (ii)

25 + x² = 4 + (x + 3)²

⇒ 25 + x² = 4 + x² + 9 + 6x

⇒ 6x = 25 – 13 = 12

⇒ x = 12/6 = 2 cm

Substituting the value of x in (i)

r² = 25 + x² = 25 + (2)² = 25 + 4

⇒ r² = 29

⇒ r = √29cm

Diameter of the circle = 2 r

= 2 ×√29 cm = 2√29 cm

10. ABC is an isosceles triangle inscribed in a circle. If AB = AC = 12√5 cm and BC = 24 cm, find the radius of the circle.

Solution 

AB = AC 12√5 and BC = 24 cm.

Join OB and OC and OA

Draw AD ⊥ BC which will pass through

Centre O

OD bisect BC in D

BD = DC = 12 cm

In right ∆ABD

AB² = AD² + BD²

⇒ (12√5)² = AD² + BD²

⇒ (12√5)² = AD² + (12)²

⇒ 144×5 =AD² + 144

⇒ 720 – 144 = AD²

⇒ AD² = 576

⇒ AD = √576 = 24

Let radius of the circle = OA = OB = OC = r

OD = AD – AO = 24 – r

Now in right ∆OBD,

OB² = BD² + OD²

⇒ r² = (12)² + (24 – r)²

⇒ r² =144 + 576 + r² – 48r

⇒ 48r = 720

⇒ 48r = 720

⇒ r = 720/48 = 48r

⇒ 48r = 720

⇒ r = 720/48 = 15cm.

Radius = 15 cm.

11. An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.

Solution 

ABC is an equilateral triangle inscribed in a

Circle with centre O. Join OB and OC,

From A, Draw AD ⊥ BC which will pass

Through the centre O of the circle.

Each side of ∆ABC = 6 cm.

AD = √3/2 a= √3/2 × 6 = 3 √3 cm.

OD = AD – AO = 3√3 – r

Now in right ∆OBD

OB² = BD² + OD²

⇒ r² = (3)² + (3√3-r)²

⇒ r² = 9 + 27 + r² -6√3r (D is mid-point of BC)

⇒ 6√3r = 36

⇒ R = 36/6√3 = 6/√3 × √3/√3 = 6√3/3 = 2√3 cm

Radius = 2√3 cm

12. AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.

Solution

AM = 18 cm and MB = 8 cm

AB = AM + MB = 18 + 8 = 26 cm

Radius of the circle = 26/2 = 13 cm

Let CD is the shortest chord drawn through M.

CD ⊥ AB

Join OC

OM = AM – AO = 18 – 13 = 5 cm

OC = OA = 13 cm

Now in right ∆OMC

OC² = OM² + MC²

⇒ (13)² = (5)² + MC² (MC² = 13² – 5²

⇒ MC² = 169 – 25 = 144 = (12)²

⇒ MC = 12

M is Mid-Point of CD

CD = 2 ×MC = 2×12 = 24 cm

Exercise 15.2

1. If arcs APB and CQD of a circle are congruent, then find the ratio of AB: CD.

Solution

arc APB = arc CQD (given)

AB = CD (If two arcs are congruent, then their corresponding chords are equal)

Ratio of AB and CD = AB / CD = AB /AB = 1/1

AB : CD = 1 : 1

2. A and B are points on a circle with centre O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.

Solution

Given : in a given circle with centre O,A

And B are Two points on the circle. C i

another point on the circle such that

∠AOC = ∠BOC

To prove : arc AC = arc BC

Proof: OC is the bisector of ∠AOB

⇒ ∠AOC = ∠BOC

But these are the angle subtended by the arc AC and BC

arc AC = arc BC.

3. Prove that the angle subtended at the centre of a circle is bisected by the radius passing through the mid-point of the arc.

Solution 

Given: AB is the arc of the circle with

Centre O and C is the mid-Point od arc AB.

To prove: OC bisects the ∠AOB

I,e ∠AOC = ∠BOC

Proof:

C is the mid-point of arc AB.

arc AC = arc BC

But arc AC and arc BC subtend ∠AOC and

∠BOC at the centre

∠AOC = ∠BOC

Hence, OC Bisects the ∠AOB.

4. In the given figure, two chords AB and CD of a circle intersect at P. If AB = CD, prove that arc AD = arc CB.

Solution 

Given: two chord AB and CD of a Circle

Intersect at P and AB = CD

To prove : arc AD = arc CB

Proof:

AB = CD (given)

minor arc AB = minor arc CD

Subtracting arc BD from both sides

arc AB = arc BD = arc CD – arc BD

⇒ arc AD = arc CD

Chapter test

1. In the given figure, a chord PQ of a circle with centre O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of : (i) PQ (ii) AP (iii) BP 

Solution

Given, radius = 15 cm

OA = OB = OP = OQ = 15 cm

Also, OM = 9 cm

MB = OB – OM = 15 – 9 = 6 cm

AM = OA + OM =15 + 9 cm = 24 cm

In ∆OMP,

By using Pythagoras Theorem,

OP² = OM ² + PM²

⇒ 15² = 9² + PM²

⇒ PM² = 255 – 81

⇒ PM = √144 = 12 cm

Also, In ∆OMQ

By using Pythagoras Theorem

OQ² = OM² + QM²

⇒ 15² = OM² + QM²

⇒ 15² = 9² + QM² (QM² = 225 – 81)

⇒ QM = √144 = 12 cm

⇒ PQ = PM + QM (As radius is bisected at M)

⇒ PQ = 12 + 12 cm = 24 cm

(ii) Now in ∆APM

AP² = AM² + OM²

⇒ AP² =24² + 12²

⇒ AP² = 576 + 144

⇒ AP = √720 = 12 √5 cm

(iii) Now in ∆BMP

BP² = BM² + PM²

BP² = 6² + 12²

⇒ BP² = 36 + 144

⇒ BP = √180 = 6√5 cm

2. The radii of two concentric circles are 17 cm and 10 cm ; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.

Solution 

A line PQRS intersects the outer circle at P

And S and inner circle at Q and R radius of

Outer circle OP = 17 cm and radius of inner

Circle OQ = 10 cm

QR = 12 cm

From O, draw OM ⊥ PS

QM = ½ QR = ½ × 12 = 6 cm

In right ∆OQM

OQ² = OM² + QM²

⇒ (10)² = OM² + (6)²

⇒ OM² = 10² – 6²

⇒ OM² = 100 – 36 = 64 = (8)²

⇒ OM = 8 cm

Now in right ∆OPM

OP² OM² + PM²

⇒ (17)² = OM² + PM²

⇒ PM² = (17)² – (8)²

⇒ PM² = 289 – 64 = 225 = (15)²

⇒ PM = 15 cm

⇒ PQ = PM – QM = 15 – 6 = 9 cm