ICSE Solutions for Chapter 17 Circles Class 10 Mathematics
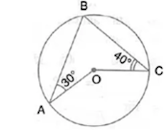
Solution 1:
Let ∠OAC = ∠OCA = x (say)
∴ ∠AOC = 180˚ – 2x
Also, ∠BAC = 30˚ + x
∠BCA = 40˚ + x
In ΔABC,
∠ABC = 180˚ - ∠BAC - ∠BCA
= 180 – (30˚ + x) – (40˚ + x) = 110˚ – 2x
Now, ∠AOC = 2∠ABC ...(Angle at the centre is double the angle at the circumference subtended by the same chord)
⇒ 180˚ – 2x = 2(110˚ – 2x)
⇒ 2x = 40˚
∴ x = 20˚
∴ ∠AOC = 180˚ – 2×20˚ = 140˚
Question 2: In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.
Solution 2: (i) In ΔABD,
∠DAB + ∠ABD + ∠ADB = 180°
⇒ 65° +70° + ∠ADB = 180°
⇒ 135° + ∠ADB = 180°
⇒ ADB = 180° - 135° = 45°
Now, ∠ADC = ∠ADB + ∠BDC = 45° + 45°= 90°
Since, ∠ADC is the angle of semicircle, so AC is a diameter of the circle.
(ii) ∠ACB = ∠ADB ….(angles in the same segment of the circle)
⇒ ∠ACB = 45°
Question 3: Given O is the centre of the circle and ∠AOB = 70˚. Calculate the value of:
(i) ∠OCA; (ii) ∠OAC.
Solution 3:
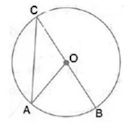Here, ∠AOB = 2∠ACB ...(Angle at the centre is double the angle at the circumference subtended by the same chord)
⇒ ∠ACB = 70°/2 = 35°
Now, OC = OA ...(Radii of same circle)
⇒ ∠OCA = ∠OAC = 35˚
Question 4: In each of the following figures, O is the centre of the circle. Find the values of a, b and c.
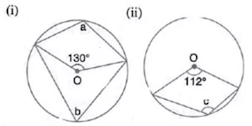
Solution 4:
Here, b = ½×130˚ ...(Angle at the centre is double the angle at the circumference subtended by the same chord)
⇒ b = 65˚
Now, a + b = 180° ...(Opposite angles of a cyclic quadrilateral are supplementary)
⇒ a = 180° - 65° = 115˚
(ii) Here, c = ½ Reflex (112˚) ...(Angle at the centre is double the angle at the circumference subtended by the same chord)
⇒ c = ½×(360° - 112˚) = 124˚
Question 5: In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. calculate the sizes of:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABC.
Solution 5: (i) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠ACB = 1/2 ∠AOB
Since AB is the side of a regular hexagon,
∠AOB = 60°
⇒ ∠ACB = 45°
Question 3: Given O is the centre of the circle and ∠AOB = 70˚. Calculate the value of:
(i) ∠OCA; (ii) ∠OAC.
Solution 3:
⇒ ∠ACB = 70°/2 = 35°
Now, OC = OA ...(Radii of same circle)
⇒ ∠OCA = ∠OAC = 35˚
Question 4: In each of the following figures, O is the centre of the circle. Find the values of a, b and c.
Solution 4:
⇒ b = 65˚
Now, a + b = 180° ...(Opposite angles of a cyclic quadrilateral are supplementary)
⇒ a = 180° - 65° = 115˚
(ii) Here, c = ½ Reflex (112˚) ...(Angle at the centre is double the angle at the circumference subtended by the same chord)
⇒ c = ½×(360° - 112˚) = 124˚
Question 5: In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. calculate the sizes of:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABC.
Solution 5: (i) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠ACB = 1/2 ∠AOB
Since AB is the side of a regular hexagon,
∠AOB = 60°
(ii) ∠AOB = 60˚
⇒ ∠ACB = ½×60° = 30°
(iii) Since AC is the side of a regular octagon,
∠AOC = 360˚/8 = 45°
Again, Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
⇒ ∠ABC = 1/2∠AOC
⇒ ABC = 45°/2 = 22.5˚
Question 6: In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angel ADC.
Solution 6:
Arc AE subtends ∠AOE at the centre and ∠ADE at the remaining part of the circle.
∴ ∠ADE = ½ ∠AOE
= ½×72˚
= 36˚ [central angle of a regular pentagon at O]
∠ADC = ∠ADB + ∠BDC
= 36° + 36° + 72˚
∴ ∠ADE : ∠ADC = 36°:72° = 1:2
Question 7: In the figure, given below, find
(i) ∠BCD, (ii) ∠ADC, (iii) ∠ABC. Show steps of your working.
Solution 7:
(i) ∠BCD + ∠BAD = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠BCD = 180° - 105° = 75˚
∠AOC = 360˚/8 = 45°
Again, Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
⇒ ∠ABC = 1/2∠AOC
⇒ ABC = 45°/2 = 22.5˚
Question 6: In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angel ADC.
Solution 6:
∴ ∠ADE = ½ ∠AOE
= ½×72˚
= 36˚ [central angle of a regular pentagon at O]
∠ADC = ∠ADB + ∠BDC
= 36° + 36° + 72˚
∴ ∠ADE : ∠ADC = 36°:72° = 1:2
Question 7: In the figure, given below, find
(i) ∠BCD, (ii) ∠ADC, (iii) ∠ABC. Show steps of your working.
Solution 7:
(Sum of opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠BCD = 180° - 105° = 75˚
(ii) Now, AB || CD
∴ ∠BAD + ∠ADC = 180°
(Interior angles on same side of parallel lines is 180°)
⇒ ∠ADC = 180° - 105° = 75˚
∴ ∠BAD + ∠ADC = 180°
(Interior angles on same side of parallel lines is 180°)
⇒ ∠ADC = 180° - 105° = 75˚
(iii) ∠ADC + ∠ABC = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠ABC = 180° - 75° = 105˚
Question 8: In the figure, given below, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find :
(i) ∠ACB; (ii) ∠OBC; (iii) ∠OAB ; (iv) ∠CBA.
Solution 8:
Here, ∠ACB = ½ Reflex (∠AOB) = ½(360° - 140°) = 110°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
Now, OA = OB ...(Radii of same circle)
∴ ∠OBA = ∠OAB = (180° - 140˚)/2 = 20˚
∴ ∠CAB = 50° - 20° = 30˚
In ΔCAB,
∠CBA = 180° - 110° - 30° = 40°
∴ ∠OBC = ∠CBA + ∠OBA = 40° + 20° = 60˚
Question 9: Calculate :
(i) ∠CDB, (ii) ∠ABC, (iii) ∠ACB.
Solution 9:
Here, ∠CDB = ∠BAC = 49˚
∠ABC - ∠ADC = 43° ...(Angles subtended by the same chord on the circle are equal)
By angle-sum property of a triangle,
∠ACB = 180° - 49° - 43° = 88°
Question 10: In the figure given below, ABCD is a cyclic quadrilateral in which ∠BAD= 75°: ∠ABD = 58° and ∠ADC = 77˚.
Find: (i) ∠BDC, (ii) ∠BCD, (iii) ∠BCA.
Solution 10:
(i) By angle – sum property of triangle ABD,
∠ADB = 180° - 75˚ - 58˚ = 47˚
∠BDC = ∠ADC - ∠ADB = 770 - 47° = 30°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠ABC = 180° - 75° = 105˚
Question 8: In the figure, given below, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find :
(i) ∠ACB; (ii) ∠OBC; (iii) ∠OAB ; (iv) ∠CBA.
Solution 8:
(Angle at the centre is double the angle at the circumference subtended by the same chord)
Now, OA = OB ...(Radii of same circle)
∴ ∠OBA = ∠OAB = (180° - 140˚)/2 = 20˚
∴ ∠CAB = 50° - 20° = 30˚
In ΔCAB,
∠CBA = 180° - 110° - 30° = 40°
∴ ∠OBC = ∠CBA + ∠OBA = 40° + 20° = 60˚
Question 9: Calculate :
(i) ∠CDB, (ii) ∠ABC, (iii) ∠ACB.
Solution 9:
∠ABC - ∠ADC = 43° ...(Angles subtended by the same chord on the circle are equal)
By angle-sum property of a triangle,
∠ACB = 180° - 49° - 43° = 88°
Question 10: In the figure given below, ABCD is a cyclic quadrilateral in which ∠BAD= 75°: ∠ABD = 58° and ∠ADC = 77˚.
Find: (i) ∠BDC, (ii) ∠BCD, (iii) ∠BCA.
Solution 10:
∠ADB = 180° - 75˚ - 58˚ = 47˚
∠BDC = ∠ADC - ∠ADB = 770 - 47° = 30°
(ii) ∠BAD + ∠BCD = 180° (Sum of opposite angles of a cyclic quadrilateral is 180°)
⇒ ∠BCD = 180° - 75˚ = 105˚
⇒ ∠BCD = 180° - 75˚ = 105˚
(iii) ∠BCA = ∠ADB = 47˚
(Angles subtended by the same chord on the circle are equal)
(Angles subtended by the same chord on the circle are equal)