Chapter 16 Loci (Locus and its Construction) Question and Answers Class 10 Mathematics

ICSE Solutions for Chapter 16 Loci (Locus and its Construction) Class 10 Mathematics

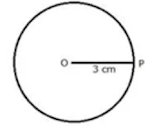
Question 1: Describe the locus of a point at a distance of 3 cm from a fixed point. 

Solution 1:

The locus of a point which is 3 cm away from a fixed point is circumference of a circle whose radius is 3 cm and the fixed point is the centre of the circle.

Question 2: Describe the locus of a point at a distance of 2 cm from a fixed line. 

Solution 2:

The locus of a point at a distance of 2 cm from a fixed line AB is a pair of straight lines I and m which are parallel to the given line at a distance of 2 cm.

Question 3: Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.

Prove: i) X is equidistant from AB and AC. 
ii) Y is equidistant from A and C

Solution 3:

Construction: From X, draw XL ⊥ AC and XM ⊥ AB. Also join YC.
Proof:
(i) In ΔAXL and ΔAXM.
∠XAL = ∠XAM ...(Given)
AX = AX ...(Common)
∠XLA = ∠XMA ...(Each = 90°)

∴ By Angle-Side-Angle criterion of congruence,
ΔAXL ≅ ΔAXM ...(ASA Postulate)

The corresponding parts of the congruent triangles are congruent.
∴  XL = XM ...(CPCT)

Hence, X is equidistant from AB and AC.

(ii) In ΔYTA and ΔYTC
AT = CT  ...(∵ PQ is a perpendicular bisector of AC)
∠YTA = ∠YTC ...(Each = 90°)

YT = YT ...(Common)

∴ By Side-Angle-Side criterion of congruence,
∴ ΔYTA ≅ ΔYTC ...(SAS Postulate)

The corresponding parts of the congruent triangles are congruent.
∴ YA = YC ...(CPCT)

Hence, Y is equidistant from A and C.

Question 4: Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that is equidistant from B and C. 

Solution 4: Given: In triangle ABC, AB = 4.2 cm, BC  = 6.3 cm and AC = 5 cm

Steps of Construction:
(i) Draw a line segment BC = 6.3 cm
(ii) With centre B and radius 4.2 cm, draw an arc.
(iii) With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
(iv) Join AB and AC. ΔABC is the required triangle.
(v) Again with centre B and C and radius greater than ½ BC, draw arcs which intersect each other at L and M.
(vi) Join LM intersecting AC at D and BC at E.
(vii) Join DB.

Proof:  In ΔDBE and ΔDCE
BE = EC ...(LM is bisector of BC)

∠DEB = ∠DEC ...(Each = 90˚)

DE = DE  ...(Common)

∴ By  Side – Angle – Side criterion of congruence, we have
ΔDBE ≅ ΔDCE  ...(SAS Postulate)
The corresponding parts of the congruent triangles are congruent.
∴  DB = DC ...(CPCT)

Hence, D is equidistant from B and C.

Question 5: Describe the locus of a stone dropped from the top of a tower. 

Solution 5:

The locus of a stone which is dropped from the top of a tower will be a vertical line through the point from which the stone is dropped.

Question 6: Describe the locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge. 

Solution 6:

The locus of the runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge will be the circumference of a circle whose radius is equal to the radius of the inner circular track plus 1.5 m.

Question 7: Describe the locus of the door handle as the door opens. 

Solution 7:

The locus of the door handle will be the circumference of a circle with centre at the axis of rotation of the door and radius equal to the distance between the door handle and the axis of rotation of the door.

Question 8: Describe the locus of a point inside a circle and equidistant from two fixed points on the circumference of the circle.

Solution 8:

The locus of the points inside the circle which are equidistant from the fixed points on the circumference of a circle will be diameter which is perpendicular bisector of the line joining the two fixed points on the circle.

Question 9: In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. 
Prove that:
(i) point A is equidistant from all the three sides of the triangle 
(ii) AM bisects angle LMN. 

Solution 9:

Construction: Join AM
Proof:
∵ A lies on bisector of ∠N
∴ A is equidistant from MN and LN
Again, A lies on bisector of ∠L
∴ A is equidistant from LN and LM.
Hence, A is equidistant from all sides of the triangle LMN.
∴ A lies on the bisector of ∠M

Question 10:
Use ruler and compasses only for this question.
(i) Construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60° 
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC. 
(iii) Construct the locus of points inside the triangle which are equidistant from B and C. 
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.

Solution 10:
Steps of construction:
(i) Draw line BC = 6 cm and an angle CBX = 60°. Cut off AB = 3.5. Join AC, triangle ABC is the required triangle.
(ii) Draw perpendicular bisector of BC and bisector of angle B.
(iii) Bisector of angle B meets bisector of BC at P.
BP is the required length, where, PB = 3.5 cm
(iv) P is the point which is equidistant from BA and BC, also equidistant from B and C.