Selina Concise Solutions for Chapter 6 Sets Class 8 ICSE Mathematics
Exercise 6 A
1. Write the following sets in roster (Tabular) form :
(i) A1 = {x : 2x + 3 = 11}
(ii) A2 = {x : x2 – 4x – 5 = 0}
(iii) A3 = {x : x ∈ Z, -3 ≤ x < 4}
(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
(vi) A6 = {x : x = n/(n + 2) ; n ∈ N and n > 5}
Solution
(i) A1 = {x : 2x + 3 = 11}
∴ 2x + 3 = 11
⇒ 2x = 11 – 3
⇒ 2x = 8
⇒ x = 8/2 ⇒ x = 4
∴ Given set in roster (Tabular) form is
A1 = {4}
(ii) A2 = {x : x2 – 4x – 5 = 0}
∴ x2 – 4x – 5 = 0
⇒ x2 – 5x + x – 5 = 0
⇒ x(x – 5) + 1(x – 5) =0
⇒ (x – 5)(x + 1) = 0
∴ Either x – 5 = 0 or x + 1 = 0
⇒ x = 5 ⇒ x = -1
∴ Given set in roster (Tabular) form is A2 = {5, -1}
(iii) A3 = {x : x ∈ Z, -3 ≤ x < 4}
∵ -3 ≤ x < 4
∴ x = -3, -2, -1, 0, 1, 2, 3
∴ Given set in roster (Tabular) form is
A3 = {-3, -2, -1, 0, 1, 2, 3}
(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
∵ x is a two digit number and sum of digits of x is 7
∴ x = 16, 25, 34, 43, 52, 61, 70
∴ Given set in roster (Tabular) form is
A4 = {16, 25, 34, 43, 52, 61, 70}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
∵ x = 4n
∴ When n = 0, x = 4 × 0
⇒ x = 0
When n = 1, x = 4 × 1
⇒ x = 4
When n = 2, x = 4 × 2
⇒ x = 8
When n = 3, x = 4 × 3
⇒ x = 12
∴ Given set in roster (Tabular) form is
A5 = {0, 4, 8, 12}
(vi) A6 = {x : x = n/(n + 2); n ∈ N & n > 5}
∵ x = n/(n + 2)
∴ When n = 6, x = 6/(6 + 2)
⇒ x = 6/8
(i) A1 = {x : 2x + 3 = 11}
(ii) A2 = {x : x2 – 4x – 5 = 0}
(iii) A3 = {x : x ∈ Z, -3 ≤ x < 4}
(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
(vi) A6 = {x : x = n/(n + 2) ; n ∈ N and n > 5}
Solution
(i) A1 = {x : 2x + 3 = 11}
∴ 2x + 3 = 11
⇒ 2x = 11 – 3
⇒ 2x = 8
⇒ x = 8/2 ⇒ x = 4
∴ Given set in roster (Tabular) form is
A1 = {4}
(ii) A2 = {x : x2 – 4x – 5 = 0}
∴ x2 – 4x – 5 = 0
⇒ x2 – 5x + x – 5 = 0
⇒ x(x – 5) + 1(x – 5) =0
⇒ (x – 5)(x + 1) = 0
∴ Either x – 5 = 0 or x + 1 = 0
⇒ x = 5 ⇒ x = -1
∴ Given set in roster (Tabular) form is A2 = {5, -1}
(iii) A3 = {x : x ∈ Z, -3 ≤ x < 4}
∵ -3 ≤ x < 4
∴ x = -3, -2, -1, 0, 1, 2, 3
∴ Given set in roster (Tabular) form is
A3 = {-3, -2, -1, 0, 1, 2, 3}
(iv) A4 = {x : x is a two digit number and sum of digits of x is 7}
∵ x is a two digit number and sum of digits of x is 7
∴ x = 16, 25, 34, 43, 52, 61, 70
∴ Given set in roster (Tabular) form is
A4 = {16, 25, 34, 43, 52, 61, 70}
(v) A5 = {x : x = 4n, n ∈ W and n < 4}
∵ x = 4n
∴ When n = 0, x = 4 × 0
⇒ x = 0
When n = 1, x = 4 × 1
⇒ x = 4
When n = 2, x = 4 × 2
⇒ x = 8
When n = 3, x = 4 × 3
⇒ x = 12
∴ Given set in roster (Tabular) form is
A5 = {0, 4, 8, 12}
(vi) A6 = {x : x = n/(n + 2); n ∈ N & n > 5}
∵ x = n/(n + 2)
∴ When n = 6, x = 6/(6 + 2)
⇒ x = 6/8
⇒ x = ¾
When n = 7, x = 7/(7 + 2)
When n = 7, x = 7/(7 + 2)
⇒ x = 7/9
When n = 8, x = 8/(8 + 2)
When n = 8, x = 8/(8 + 2)
⇒ x = 8/10
⇒ x = 4/5
When n = 9, x = 9/(9 + 2)
⇒ x = 4/5
When n = 9, x = 9/(9 + 2)
⇒ x = 9/11
∴ Given set in roster (Tabular) form is
A6 = {3/4, 7/9, 4/5, 9/11,…}
2. Write the following sets in set-builder (Rule Method) form:
(i) B1 = {6, 9, 2, 15, ...}
(ii) B2 = {11, 13, 17, 19 }
(iii) B3 = (1/3, 3/5, 5/7, 7/9, 9/11,…}
(iv) B4 = {8, 27, 64, 125, 216}
(v) B5 = {-5, -4, -3, -2, -1}
(vi) B6 = {…, -6, -3, 0, 3, 6 ….}
Solution
(i) B1 = {6, 9, 12, 15, ….}
= {x : x = 3n + 3; n ∈ N}
(ii) B2 = {11, 13, 17, 19}
= {x : x is a prime number between 10 and 20}
(iii) B3 = {1/3, 3/5, 5/7, 7/9, 9/11, …}
= {x : x = n/(n + 2), where n is an odd natural number}
(iv) B4 = {8, 27, 64, 125, 216}
= {x : x = n3; n ∈ N and 2 ≤ n ≤ 6}
(v) B5 = {-5, -4, -3, -2, -1}
= {x : x ∈ Z, -5 ≤ x ≤ -1}
(vi) B6 = {…, -6, -3, 0, 3, 6, …}
= {x : x = 3n, n ∈ Z}
3. (i) Is {1, 2, 4, 16, 64} = {x : x is a factor of 32} ? Give reason.
(ii) Is {x : x is a factor of 27} ≠ {3, 9, 27, 54}? Give reason.
(iii) Write the set of even factors of 124.
(iv) Write the set of odd factors of 72.
(v) Write the set of prime factors of 3234.
(vi) Is {x : x2 – 7x + 12 = 0} = {3, 4} ?
(vii) Is {x : x2 – 5x – 6 = 0} = {2, 3} ?
Solution
(i) No, {1, 2, 4, 16, 64} ≠ {x : x is a factor of 32}
Because 64 is not a factor of 32
(ii) Yes, { x : x is a factor of 27} + {3, 9, 27, 54}
Because 54 is not a factor of 27
(iii) 1 × 124 = 124
2 × 62 = 124
4 × 31 = 124
Factors of 124 = 1, 2, 4, 31, 62, 124
Set of even factors 124 = {2, 4, 62, 124}
(iv) 1 × 172 = 72
2 × 36 = 72
3 × 24 = 72
4 × 18 = 72
6 ×12 = 72
8 × 9 = 72
Factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Set of odd factors of 72 = {1, 3, 9}
(v)
3234 = 2 × 3 × 7 × 7 × 11
∴ Set of prime factors of 3234 = {2, 3, 7, 11}
(vi) x2 – 7x + 12 = 0
⇒ x2 – 4x – 3x + 12 = 0
⇒ x(x – 4) – 3(x – 4) = 0
⇒ (x – 4)(x – 3) = 0
∴ Either x – 4 = 0 or x – 3 = 0
⇒ x = 4 ⇒ x = 3
∴ {x : x2 – 7x + 12 = 0} = {3, 4} is true
(vii) x2 – 5x – 6 = 0
⇒ x2 – 6x + x – 6 = 0
⇒ x(x – 6) + 1(x – 6) = 0
⇒ (x - 6)(x + 1) = 0
∴ Either x – 6 = 0 or x + 1 = 0
i.e., x = 6 i.e., x = -1
∴ {x : x2 - 5x – 6 = 0} ≠ {2, 3}
In other words {x : x2 – 5x – 6 = 0} = {2, 3} is not true
4. Write the following sets in Roster form:
(i) The set of letters in the word ‘MEERUT’.
(ii) The set of letters in the word ‘UNIVERSAL’.
(iii) A = {x : x = y + 3, y ∈ N and y > 3}
(iv) B = {p : p ∈ W and p2 < 20}
(v) C = {x : x is composite number and 5 < x < 21}
Solution
(i) Roster form of the set of letters in the word “MEERUT” = {m, e, r, u, t}
(ii) Roster form of the set of letters in the word “UNIVERSAL” = {u, n, i, v, e, r, s, a, l}
(iii) A = {x : x = y + 3, y ∈ N and y > 3}
x = y + 3
when y = 4, x = 4 +3 = 7
when y = 5, x = 5 + 3 = 8
when y = 6, x = 6 + 3 = 9
when y = 7, x = 7 + 3 = 10
when y = 8, x = 8 + 3 = 11
∴ Roster form of the given set A = {7, 8, 9, 10, 11 ……}
(iv) B = {P : P ∈ W and p2 < 20}
When P2 = 0
P = √0 = 0
When P2 = 1
P = √1 = 1
When P2 = 4
P = √4 = 2
When P2 = 9
P = √9 = 3
When P2 = 16
P = √16 = 4
∴ Roster form of the given set B = {0, 1, 2, 3, 4}
(v) C = {x : x is composite number and 5 ≤ x ≤ 21}
5 ≤ x ≤ 21 means x = 5, 6, 7, 8, 9, 10, ……, 21
But we are given that x is a composite number
∴ x = 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21
∴ Roster form of the given set C = {6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21}
Note: Composite numbers: The natural numbers (greater than 1), which are not prime, are called composite numbers.
5. List the elements of the following sets:
(i) {x : x2 – 2x – 3 = 0}
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
(iii) {x : x is a factor of 24}
(iv) {x : x ∈ Z and x2 ≤ 4}
(v) {x : 3x – 2 ≤ 10, x ∈ N}
(vi) { x : 4 – 2x > -6, x ∈ Z}
Solution
(i){x : x2 - 2x – 3 = 0}
x2 – 2x – 3 = 0
⇒ x2 – 3x + x – 3 = 0
⇒ x(x – 3) + 1(x – 3) = 0
⇒ (x + 1)(x – 3) = 0
∴ Either x – 3 = 0 or x + 1 = 0
x = 3 or x = -1
∴ Elements of the set :{x : x2 – 2x – 3 = 0} are 3 and -1
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
x = 2y + 5
when y = 2, x = 2 × 2 + 5 = 4 + 5 = 9
When y = 3, x = 2 × 3 + 5 = 6 + 5 = 11
When y = 4, x = 2 × 4 + 5 = 8 + 5 = 13
When y = 5, x = 2 × 5 + 5 = 10 + 5 = 15
∴ Elements of the given set {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6} are 9, 11, 13, 15
(iii) {x : x is a factor of 24}
24 = 1 × 24
24 = 2 × 12
24 = 3 × 8
24 = 4 × 6
∴ Elements of the given set { x : x is a factor of 24} are 1, 2, 3, 4, 6, 8, 12, 24
(iv) {x : x ∈ Z and x2 ≤ 4}
When x2 = 4
x = ± √4 = ± 2
when x2 = 1
x = ± √1 = ±1
when x2 = 0
x = √0 = 0
∴ Elements of the given set {x : x ∈ Z and x2 ≤ 4 are +2, -2, + 1, -1, 0 or are -2, -1, 0, 1, 2
(v) {x : 3x – 2 ≤ 10, x ∈ N}
3x – 2 ≤ 10
⇒ 3x ≤ 10 + 2
⇒ 3x ≤ 12
⇒ x ≤ 12/3
≤ x ≤ 4
∴ Elements of the given set {x : 3x – 2 ≤ 10, x ∈ N} are 1, 2, 3 and 4
(vi) {x : 4 – 2x > -6, x ∈ Z}
4 – 2x > -6
⇒ -4 + 4 – 2x > -6 - 4 (Subtracting 4 from both sides)
⇒ -2x > -10
⇒ -2x + 2x + 10 > -10 + 2x + 10 [Adding 2x + 10 to both sides]
⇒ + 10 > 2x
∴ Given set in roster (Tabular) form is
A6 = {3/4, 7/9, 4/5, 9/11,…}
2. Write the following sets in set-builder (Rule Method) form:
(i) B1 = {6, 9, 2, 15, ...}
(ii) B2 = {11, 13, 17, 19 }
(iii) B3 = (1/3, 3/5, 5/7, 7/9, 9/11,…}
(iv) B4 = {8, 27, 64, 125, 216}
(v) B5 = {-5, -4, -3, -2, -1}
(vi) B6 = {…, -6, -3, 0, 3, 6 ….}
Solution
(i) B1 = {6, 9, 12, 15, ….}
= {x : x = 3n + 3; n ∈ N}
(ii) B2 = {11, 13, 17, 19}
= {x : x is a prime number between 10 and 20}
(iii) B3 = {1/3, 3/5, 5/7, 7/9, 9/11, …}
= {x : x = n/(n + 2), where n is an odd natural number}
(iv) B4 = {8, 27, 64, 125, 216}
= {x : x = n3; n ∈ N and 2 ≤ n ≤ 6}
(v) B5 = {-5, -4, -3, -2, -1}
= {x : x ∈ Z, -5 ≤ x ≤ -1}
(vi) B6 = {…, -6, -3, 0, 3, 6, …}
= {x : x = 3n, n ∈ Z}
3. (i) Is {1, 2, 4, 16, 64} = {x : x is a factor of 32} ? Give reason.
(ii) Is {x : x is a factor of 27} ≠ {3, 9, 27, 54}? Give reason.
(iii) Write the set of even factors of 124.
(iv) Write the set of odd factors of 72.
(v) Write the set of prime factors of 3234.
(vi) Is {x : x2 – 7x + 12 = 0} = {3, 4} ?
(vii) Is {x : x2 – 5x – 6 = 0} = {2, 3} ?
Solution
(i) No, {1, 2, 4, 16, 64} ≠ {x : x is a factor of 32}
Because 64 is not a factor of 32
(ii) Yes, { x : x is a factor of 27} + {3, 9, 27, 54}
Because 54 is not a factor of 27
(iii) 1 × 124 = 124
2 × 62 = 124
4 × 31 = 124
Factors of 124 = 1, 2, 4, 31, 62, 124
Set of even factors 124 = {2, 4, 62, 124}
(iv) 1 × 172 = 72
2 × 36 = 72
3 × 24 = 72
4 × 18 = 72
6 ×12 = 72
8 × 9 = 72
Factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Set of odd factors of 72 = {1, 3, 9}
(v)
∴ Set of prime factors of 3234 = {2, 3, 7, 11}
(vi) x2 – 7x + 12 = 0
⇒ x2 – 4x – 3x + 12 = 0
⇒ x(x – 4) – 3(x – 4) = 0
⇒ (x – 4)(x – 3) = 0
∴ Either x – 4 = 0 or x – 3 = 0
⇒ x = 4 ⇒ x = 3
∴ {x : x2 – 7x + 12 = 0} = {3, 4} is true
(vii) x2 – 5x – 6 = 0
⇒ x2 – 6x + x – 6 = 0
⇒ x(x – 6) + 1(x – 6) = 0
⇒ (x - 6)(x + 1) = 0
∴ Either x – 6 = 0 or x + 1 = 0
i.e., x = 6 i.e., x = -1
∴ {x : x2 - 5x – 6 = 0} ≠ {2, 3}
In other words {x : x2 – 5x – 6 = 0} = {2, 3} is not true
4. Write the following sets in Roster form:
(i) The set of letters in the word ‘MEERUT’.
(ii) The set of letters in the word ‘UNIVERSAL’.
(iii) A = {x : x = y + 3, y ∈ N and y > 3}
(iv) B = {p : p ∈ W and p2 < 20}
(v) C = {x : x is composite number and 5 < x < 21}
Solution
(i) Roster form of the set of letters in the word “MEERUT” = {m, e, r, u, t}
(ii) Roster form of the set of letters in the word “UNIVERSAL” = {u, n, i, v, e, r, s, a, l}
(iii) A = {x : x = y + 3, y ∈ N and y > 3}
x = y + 3
when y = 4, x = 4 +3 = 7
when y = 5, x = 5 + 3 = 8
when y = 6, x = 6 + 3 = 9
when y = 7, x = 7 + 3 = 10
when y = 8, x = 8 + 3 = 11
∴ Roster form of the given set A = {7, 8, 9, 10, 11 ……}
(iv) B = {P : P ∈ W and p2 < 20}
When P2 = 0
P = √0 = 0
When P2 = 1
P = √1 = 1
When P2 = 4
P = √4 = 2
When P2 = 9
P = √9 = 3
When P2 = 16
P = √16 = 4
∴ Roster form of the given set B = {0, 1, 2, 3, 4}
(v) C = {x : x is composite number and 5 ≤ x ≤ 21}
5 ≤ x ≤ 21 means x = 5, 6, 7, 8, 9, 10, ……, 21
But we are given that x is a composite number
∴ x = 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21
∴ Roster form of the given set C = {6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21}
Note: Composite numbers: The natural numbers (greater than 1), which are not prime, are called composite numbers.
5. List the elements of the following sets:
(i) {x : x2 – 2x – 3 = 0}
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
(iii) {x : x is a factor of 24}
(iv) {x : x ∈ Z and x2 ≤ 4}
(v) {x : 3x – 2 ≤ 10, x ∈ N}
(vi) { x : 4 – 2x > -6, x ∈ Z}
Solution
(i){x : x2 - 2x – 3 = 0}
x2 – 2x – 3 = 0
⇒ x2 – 3x + x – 3 = 0
⇒ x(x – 3) + 1(x – 3) = 0
⇒ (x + 1)(x – 3) = 0
∴ Either x – 3 = 0 or x + 1 = 0
x = 3 or x = -1
∴ Elements of the set :{x : x2 – 2x – 3 = 0} are 3 and -1
(ii) {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}
x = 2y + 5
when y = 2, x = 2 × 2 + 5 = 4 + 5 = 9
When y = 3, x = 2 × 3 + 5 = 6 + 5 = 11
When y = 4, x = 2 × 4 + 5 = 8 + 5 = 13
When y = 5, x = 2 × 5 + 5 = 10 + 5 = 15
∴ Elements of the given set {x : x = 2y + 5; y ∈ N and 2 ≤ y < 6} are 9, 11, 13, 15
(iii) {x : x is a factor of 24}
24 = 1 × 24
24 = 2 × 12
24 = 3 × 8
24 = 4 × 6
∴ Elements of the given set { x : x is a factor of 24} are 1, 2, 3, 4, 6, 8, 12, 24
(iv) {x : x ∈ Z and x2 ≤ 4}
When x2 = 4
x = ± √4 = ± 2
when x2 = 1
x = ± √1 = ±1
when x2 = 0
x = √0 = 0
∴ Elements of the given set {x : x ∈ Z and x2 ≤ 4 are +2, -2, + 1, -1, 0 or are -2, -1, 0, 1, 2
(v) {x : 3x – 2 ≤ 10, x ∈ N}
3x – 2 ≤ 10
⇒ 3x ≤ 10 + 2
⇒ 3x ≤ 12
⇒ x ≤ 12/3
≤ x ≤ 4
∴ Elements of the given set {x : 3x – 2 ≤ 10, x ∈ N} are 1, 2, 3 and 4
(vi) {x : 4 – 2x > -6, x ∈ Z}
4 – 2x > -6
⇒ -4 + 4 – 2x > -6 - 4 (Subtracting 4 from both sides)
⇒ -2x > -10
⇒ -2x + 2x + 10 > -10 + 2x + 10 [Adding 2x + 10 to both sides]
⇒ + 10 > 2x
⇒ 10/2 > x
⇒ 5 > x
∴ Elements of the given set {x : 4 – 2x > -6, x ∈ Z} are 4, 3, 2, 1, 0, -1 …
⇒ 5 > x
∴ Elements of the given set {x : 4 – 2x > -6, x ∈ Z} are 4, 3, 2, 1, 0, -1 …
Exercise 6 B
1. Find the cardinal number of the following sets:
(i) A1 = {-2, -1, 1, 3, 5}
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
(iii) A3 = {p : p ∈ W 2p – 3 < 8}
(iv) A4 = {b : b ∈ Z and -7 < 3b - 1 ≤ 2}
Cardinal Number of a set: The number of elements in a set is called its Cardinal Number.
Solution
(i) A1 = {-2, -1, 1, 3, 5}
∴ Cardinal number of set A1 = 5
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
= {3, 4, 5, 6}
∴ Cardinal number of set A2 = 4
(iii) A3 = {P : P ∈ W and 2P - 3 < 8}
2P – 3 < 8
⇒ 2P – 3 + 3 < 8 + 3
(Adding 3 to both sides)
⇒ 2P < 11
⇒ P < 11/2 (Dividing both sides by 2)
⇒ P < 5.5
∴ A3 = {0, 1, 2, 3, 4, 5}
∴ Cardinal number of set A3 = 6
(iv) A4 = {b : b ∈ Z and – 7 < 3b – 1 ≤ 2}
-7 < 3b – 1
⇒ - 7 + 1 < 3b – 1 + 1 (Adding 1 to both sides)
⇒ -6 < 3b
⇒ -6/3 < b (Dividing both sides by 3)
⇒ -2 < b
Again 3b - 1 ≤ 2
⇒ 3b - 1 + 1 ≤ 2 + 1 (Adding 1 to both sides)
⇒ 3b ≤ 3
⇒ b ≤ 3/3 (Dividing both sides by 3)
⇒ b ≤ 1
∴ -2 ≤ b ≤ 1
∴ Given set A4 = {-1, 0, 1}
∴ Cardinal number of set A4 = 3
2. If P = {P : P is a letter in the word “PERMANENT’}. Find n(P).
Solution
P = (P : P is a letter in the word “ PERMANENT”}
Or P = {p, e, r, m, a, n, t}
n(P) = 7
3. State, which of the following sets are finite and which are infinite:
(i) A = {x : x ∈ Z and x < 10}
(ii) B = {x : x ∈ W and 5x – 3 ≤ 20}
(iii) P = {y : y = 3x – 2, x ∈ N & x > 5}
(iv) M = {r : r = 3/n; n ∈ W and 6 < n ≤ 15}
Note: (i) A set with finite (limited) number of elements in it, is called a finite set, (ii) A set which is not finite is called an infinite set.
Solution
(i) A = {x : x ∈ Z and x < 10}
= {…., -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
= {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4, ….}
∴ It is an infinite set.
(ii) B = {x : x ∈ W and 5x – 3 ≤ 20}
5x – 3 ≤ 20
⇒ 5x – 3 + 3 ≤ 20 + 3 (Adding 3 to both sides)
⇒ 5x ≤ 20 + 3
⇒ 5x ≤ 23
⇒ x ≤ 23/5 (Dividing both sides by 5)
⇒ x ≤ 4.6
∴ B = {0, 1, 2, 3, 4}
∴ It is a finite set.
(iii) P = {y : y = 3x – 2, x ∈ N and x > 5}
y = 3x – 2
When x = 6, y = 3×6 – 2 = 18 – 2 = 16
When x = 7, y = 3×7 – 2 = 21 – 2 = 19
When x = 8, y = 3 × 8 – 2 = 24 – 2 = 22
When x = 9, y = 3 × 9 – 2 = 27 – 2 = 25
∴ P = {16, 19, 22, 25, ...}
∴ It is an infinite set.
(iv) M = {r : r = 3/n; n ∈ W and 6 < n ≤ 15}
r = 3/n
when n = 7, r = 3/7
when n = 8, r = 3/8
when n = 9, r = 3/9
when n = 10, r = 3/10
when n = 11, r = 3/11
when n = 12, r = 3/12
when n = 13, r = 3/13
when n = 14, r = 3/14
when n = 15, r = 3/15
∴ M = {3/7, 3/8, 3/9, 3/10, 3/11, 3/12, 3/13, 3/14, 3/15}
∴ It is a finite set.
4. Find which of the following sets are singleton sets:
(i) The set of points of intersection of two non-parallel st. lines in the same plane.
(ii) A = {x : 7x – 3 = 11}
(iii) B = {y : 2y + 1 < 3 and y ∈ W}
Note: A set, which has only one element in it, it is called a SINGLETON or unit set.
Solution
(i) The set of points of intersection of two non-parallel st. lines in the same plane is singleton set.
(ii) A = {x : 7x – 3 = 11}
7x – 3 = 11
⇒ 7x = 11 + 3
⇒ 7x = 14
⇒ x = 14/7 = 2
∴ A = {2}
Hence, given set A is a singleton set.
(iii) B = {y : 2y + 1 < 3 and y ∈ W}
2y + 1 < 3
⇒ 2y + 1 – 1 < 3 – 1 (Subtracting 1 from both sides)
⇒ 2y < 2
⇒ y < 2/2 (Dividing both sides by 2)
⇒ y < 1
∴ B = {0}
Hence, it is singleton set.
5. Find which of the following sets are empty:
(i) The set of points of intersection of two parallel lines.
(ii) A = {x : x ∈ N and 5 < x < 6}
(iii) B = {x : x2 + 4 = 0, x ∈ N}
(iv) C = {even numbers between 7 & 11}
(v) D = {prime numbers between 7 & 11}
Note: The set, which has no element in it, is called the empty or null set.
Solution
(i) ”The set of points of intersection of two parallel lines” is an empty set because two parallel lines do not intersect anywhere.
(ii) A = { x : x ∈ N and 5 < x ≤ 6}
As 5 < x ≤ 6
∴ x = 6
∴ A = {6}
Hence, given set A is not an empty set.
(iii) B = {x : x2 + 4 = 0, x ∈ N}
x2 + 4 = 0
⇒ x2 = -4
⇒ x = √-4 which is not an empty set.
(iv) C = {Even numbers between 6 and 10}
∴ C = {8}
Hence it is not an empty set.
(v) D = {Prime numbers between 7 and 11}
Because there is no prime numbers between 7 and 11.
∴ D = { }
Hence, it is an empty set.
6. (i) Are the sets A = {4, 5, 6} and B = {x : x2 – 5x – 6 = 0} disjoint ?
(ii) Are the sets A = {b , c, d, e} and B = {x : x is a letter in the word ‘MASTER’} joint?
Note: (i)Two sets are said to be joint sets, if they have at least one element in common.
(ii) Two sets are said to be disjoint if they have no elements in common.
Solution
(i) A = {4, 5, 6}
B = {x : x2 – 5x – 6 = 0}
x2 – 5x – 6 = 0
⇒ x2 – 6x + x – 6= 0
⇒ (x – 6) + 1(x – 6) = 0
⇒ (x – 6)(x +1) = 0
∴ Either x – 6 = 0 Or x + 1 = 0
⇒ x = 6 or x = -1
∴ B = {6, -1}
Hence set A and set B are not disjoint because these sets have elements 6 in common.
(ii) A {b, c, d, e}
B = {x : x is a letter in the word “MASTER”}
∴ B = {m, a, s, t, e, r}
Hence set A and set B are joint because these sets have elements e in common.
7. State, whether the following pairs of sets are equivalent or not:
(i) A = {x : x ∈ N and 11 ≥ 2x – 1} and B = {y : y ∈ W and 3 ≤ y ≤ 9}
(ii) Set of intergers and set of natural numbers.
(iii) Set of whole numbers and set of multiples of 3.
(iv) P = {5, 6, 7, 8} and M = {x : x ∈ W and x < 4}
Note: Two sets are said to be equivalent, if they contain the same number of elements.
Solution
(i) A = {x : x ∈ N and 11 ≥ 2x – 1}
11 ≥ 2x – 1
⇒ 11 + 1 ≥ 2x – 1 + 1
⇒ 12 ≥ 2x
⇒ 12/2 ≥ x
⇒ 6 ≥ x
∴ A = {1, 2, 3, 4, 5, 6}
∴ n(A) = 6
B = {y : y ∈ W and 3 ≤ y ≤ 9}
∵ 3 ≤ y ≤ 9
B = {3, 4, 5, 6, 7, 8, 9}
n(B) = 7
Cardinal number of set A = 6 and cardinal number of set B = 7
Set A and Set B are not equivalent.
(ii) Set of integers has infinite number of elements. Set of natural numbers has infinite number of elements.
Set of integers and set of natural numbers are equivalent because both these sets have infinite number of elements.
(iii) Set of whole numbers, has infinite number of elements. Set of multiples of 3, has infinite number of element.
Set of whole numbers and set of multiples of 3 are equivalent because both these sets have infinite number of elements.
(iv) P = {5, 6, 7, 8}
n(P) = 4
M = {x : x ∈ W and x ≤ 4}
M = {0, 1, 2, 3, 4}
n(M) = 5
Now Cardinal number of set P = 4 and
Cardinal number of set M = 5
These sets are not equivalent.
8. State whether the following pairs of sets are equal or not:
(i) A = {2, 4, 6, 8} and
B = {2n : n ∈ N and n < 5}
(ii) M = {x : x ∈ W and x + 3 < 8} and
N = {y : y = 2n – 1, n ∈ N and n < 5}
(iii) E = {x : x2 + 8x – 9 = 0} and
F = {1, -9}
(iv) A = {x : x ∈ N, x < 3} and
B = {y : y2 – 3y + 2 = 0}
Note: Two sets are equal, if both the sets have same (identical) elements.
Solution
(i) A = {2, 4, 6, 8}
B = {2n : n ∈ N and n < 5}
When n = 1, 2n = 2 × 1 = 2
When n = 2, 2n = 2 × 2 = 4
When n = 3, 2n = 2 × 3 = 6
When n = 4, 2n = 2 × 4 = 8
∴ B = {2, 4, 6, 8}
Now we see that elements of sets A and B are the same (identical)
∴ Sets A and B are equal.
(ii) M = {x : x ∈ W and x + 3 < 8}
x + 3 < 8
⇒ x < 8 – 3
⇒ x < 5
∴ M = {0, 1, 2, 3, 4}
N = {y : y = 2n – 1, n ∈ N and n < 5}
y = 2n – 1
when n = 1, y = 2 × 1 – 1
⇒ y = 2 – 1 = 1
when n = 2, y = 2 × 2 – 1
⇒ y = 4 – 1 = 3
when n = 3, y = 2 × 3 – 1
⇒ y = 6 – 1 = 5
when n = 4, y = 2 × 4 – 1
⇒ y = 8 – 1 = 7
∴ N = {1, 3, 5, 7}
Now we see that elements of sets M and N are not the same (identical).
∴ Sets M and N are not equal.
(iii) E = {x : x2 + 8x – 9 = 0}
x2 + 8x – 9 = 0
⇒ x2 + 9x – x – 9 = 0
⇒ x(x + 9) – 1(x + 9) = 0
⇒ (x – 1)(x + 9) = 0
∴ Either x + 9 = 0 or x – 1 = 0
⇒ x = - 9 or x = 1
(i) A1 = {-2, -1, 1, 3, 5}
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
(iii) A3 = {p : p ∈ W 2p – 3 < 8}
(iv) A4 = {b : b ∈ Z and -7 < 3b - 1 ≤ 2}
Cardinal Number of a set: The number of elements in a set is called its Cardinal Number.
Solution
(i) A1 = {-2, -1, 1, 3, 5}
∴ Cardinal number of set A1 = 5
(ii) A2 = {x : x ∈ N and 3 ≤ x < 7}
= {3, 4, 5, 6}
∴ Cardinal number of set A2 = 4
(iii) A3 = {P : P ∈ W and 2P - 3 < 8}
2P – 3 < 8
⇒ 2P – 3 + 3 < 8 + 3
(Adding 3 to both sides)
⇒ 2P < 11
⇒ P < 11/2 (Dividing both sides by 2)
⇒ P < 5.5
∴ A3 = {0, 1, 2, 3, 4, 5}
∴ Cardinal number of set A3 = 6
(iv) A4 = {b : b ∈ Z and – 7 < 3b – 1 ≤ 2}
-7 < 3b – 1
⇒ - 7 + 1 < 3b – 1 + 1 (Adding 1 to both sides)
⇒ -6 < 3b
⇒ -6/3 < b (Dividing both sides by 3)
⇒ -2 < b
Again 3b - 1 ≤ 2
⇒ 3b - 1 + 1 ≤ 2 + 1 (Adding 1 to both sides)
⇒ 3b ≤ 3
⇒ b ≤ 3/3 (Dividing both sides by 3)
⇒ b ≤ 1
∴ -2 ≤ b ≤ 1
∴ Given set A4 = {-1, 0, 1}
∴ Cardinal number of set A4 = 3
2. If P = {P : P is a letter in the word “PERMANENT’}. Find n(P).
Solution
P = (P : P is a letter in the word “ PERMANENT”}
Or P = {p, e, r, m, a, n, t}
n(P) = 7
3. State, which of the following sets are finite and which are infinite:
(i) A = {x : x ∈ Z and x < 10}
(ii) B = {x : x ∈ W and 5x – 3 ≤ 20}
(iii) P = {y : y = 3x – 2, x ∈ N & x > 5}
(iv) M = {r : r = 3/n; n ∈ W and 6 < n ≤ 15}
Note: (i) A set with finite (limited) number of elements in it, is called a finite set, (ii) A set which is not finite is called an infinite set.
Solution
(i) A = {x : x ∈ Z and x < 10}
= {…., -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
= {9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4, ….}
∴ It is an infinite set.
(ii) B = {x : x ∈ W and 5x – 3 ≤ 20}
5x – 3 ≤ 20
⇒ 5x – 3 + 3 ≤ 20 + 3 (Adding 3 to both sides)
⇒ 5x ≤ 20 + 3
⇒ 5x ≤ 23
⇒ x ≤ 23/5 (Dividing both sides by 5)
⇒ x ≤ 4.6
∴ B = {0, 1, 2, 3, 4}
∴ It is a finite set.
(iii) P = {y : y = 3x – 2, x ∈ N and x > 5}
y = 3x – 2
When x = 6, y = 3×6 – 2 = 18 – 2 = 16
When x = 7, y = 3×7 – 2 = 21 – 2 = 19
When x = 8, y = 3 × 8 – 2 = 24 – 2 = 22
When x = 9, y = 3 × 9 – 2 = 27 – 2 = 25
∴ P = {16, 19, 22, 25, ...}
∴ It is an infinite set.
(iv) M = {r : r = 3/n; n ∈ W and 6 < n ≤ 15}
r = 3/n
when n = 7, r = 3/7
when n = 8, r = 3/8
when n = 9, r = 3/9
when n = 10, r = 3/10
when n = 11, r = 3/11
when n = 12, r = 3/12
when n = 13, r = 3/13
when n = 14, r = 3/14
when n = 15, r = 3/15
∴ M = {3/7, 3/8, 3/9, 3/10, 3/11, 3/12, 3/13, 3/14, 3/15}
∴ It is a finite set.
4. Find which of the following sets are singleton sets:
(i) The set of points of intersection of two non-parallel st. lines in the same plane.
(ii) A = {x : 7x – 3 = 11}
(iii) B = {y : 2y + 1 < 3 and y ∈ W}
Note: A set, which has only one element in it, it is called a SINGLETON or unit set.
Solution
(i) The set of points of intersection of two non-parallel st. lines in the same plane is singleton set.
(ii) A = {x : 7x – 3 = 11}
7x – 3 = 11
⇒ 7x = 11 + 3
⇒ 7x = 14
⇒ x = 14/7 = 2
∴ A = {2}
Hence, given set A is a singleton set.
(iii) B = {y : 2y + 1 < 3 and y ∈ W}
2y + 1 < 3
⇒ 2y + 1 – 1 < 3 – 1 (Subtracting 1 from both sides)
⇒ 2y < 2
⇒ y < 2/2 (Dividing both sides by 2)
⇒ y < 1
∴ B = {0}
Hence, it is singleton set.
5. Find which of the following sets are empty:
(i) The set of points of intersection of two parallel lines.
(ii) A = {x : x ∈ N and 5 < x < 6}
(iii) B = {x : x2 + 4 = 0, x ∈ N}
(iv) C = {even numbers between 7 & 11}
(v) D = {prime numbers between 7 & 11}
Note: The set, which has no element in it, is called the empty or null set.
Solution
(i) ”The set of points of intersection of two parallel lines” is an empty set because two parallel lines do not intersect anywhere.
(ii) A = { x : x ∈ N and 5 < x ≤ 6}
As 5 < x ≤ 6
∴ x = 6
∴ A = {6}
Hence, given set A is not an empty set.
(iii) B = {x : x2 + 4 = 0, x ∈ N}
x2 + 4 = 0
⇒ x2 = -4
⇒ x = √-4 which is not an empty set.
(iv) C = {Even numbers between 6 and 10}
∴ C = {8}
Hence it is not an empty set.
(v) D = {Prime numbers between 7 and 11}
Because there is no prime numbers between 7 and 11.
∴ D = { }
Hence, it is an empty set.
6. (i) Are the sets A = {4, 5, 6} and B = {x : x2 – 5x – 6 = 0} disjoint ?
(ii) Are the sets A = {b , c, d, e} and B = {x : x is a letter in the word ‘MASTER’} joint?
Note: (i)Two sets are said to be joint sets, if they have at least one element in common.
(ii) Two sets are said to be disjoint if they have no elements in common.
Solution
(i) A = {4, 5, 6}
B = {x : x2 – 5x – 6 = 0}
x2 – 5x – 6 = 0
⇒ x2 – 6x + x – 6= 0
⇒ (x – 6) + 1(x – 6) = 0
⇒ (x – 6)(x +1) = 0
∴ Either x – 6 = 0 Or x + 1 = 0
⇒ x = 6 or x = -1
∴ B = {6, -1}
Hence set A and set B are not disjoint because these sets have elements 6 in common.
(ii) A {b, c, d, e}
B = {x : x is a letter in the word “MASTER”}
∴ B = {m, a, s, t, e, r}
Hence set A and set B are joint because these sets have elements e in common.
7. State, whether the following pairs of sets are equivalent or not:
(i) A = {x : x ∈ N and 11 ≥ 2x – 1} and B = {y : y ∈ W and 3 ≤ y ≤ 9}
(ii) Set of intergers and set of natural numbers.
(iii) Set of whole numbers and set of multiples of 3.
(iv) P = {5, 6, 7, 8} and M = {x : x ∈ W and x < 4}
Note: Two sets are said to be equivalent, if they contain the same number of elements.
Solution
(i) A = {x : x ∈ N and 11 ≥ 2x – 1}
11 ≥ 2x – 1
⇒ 11 + 1 ≥ 2x – 1 + 1
⇒ 12 ≥ 2x
⇒ 12/2 ≥ x
⇒ 6 ≥ x
∴ A = {1, 2, 3, 4, 5, 6}
∴ n(A) = 6
B = {y : y ∈ W and 3 ≤ y ≤ 9}
∵ 3 ≤ y ≤ 9
B = {3, 4, 5, 6, 7, 8, 9}
n(B) = 7
Cardinal number of set A = 6 and cardinal number of set B = 7
Set A and Set B are not equivalent.
(ii) Set of integers has infinite number of elements. Set of natural numbers has infinite number of elements.
Set of integers and set of natural numbers are equivalent because both these sets have infinite number of elements.
(iii) Set of whole numbers, has infinite number of elements. Set of multiples of 3, has infinite number of element.
Set of whole numbers and set of multiples of 3 are equivalent because both these sets have infinite number of elements.
(iv) P = {5, 6, 7, 8}
n(P) = 4
M = {x : x ∈ W and x ≤ 4}
M = {0, 1, 2, 3, 4}
n(M) = 5
Now Cardinal number of set P = 4 and
Cardinal number of set M = 5
These sets are not equivalent.
8. State whether the following pairs of sets are equal or not:
(i) A = {2, 4, 6, 8} and
B = {2n : n ∈ N and n < 5}
(ii) M = {x : x ∈ W and x + 3 < 8} and
N = {y : y = 2n – 1, n ∈ N and n < 5}
(iii) E = {x : x2 + 8x – 9 = 0} and
F = {1, -9}
(iv) A = {x : x ∈ N, x < 3} and
B = {y : y2 – 3y + 2 = 0}
Note: Two sets are equal, if both the sets have same (identical) elements.
Solution
(i) A = {2, 4, 6, 8}
B = {2n : n ∈ N and n < 5}
When n = 1, 2n = 2 × 1 = 2
When n = 2, 2n = 2 × 2 = 4
When n = 3, 2n = 2 × 3 = 6
When n = 4, 2n = 2 × 4 = 8
∴ B = {2, 4, 6, 8}
Now we see that elements of sets A and B are the same (identical)
∴ Sets A and B are equal.
(ii) M = {x : x ∈ W and x + 3 < 8}
x + 3 < 8
⇒ x < 8 – 3
⇒ x < 5
∴ M = {0, 1, 2, 3, 4}
N = {y : y = 2n – 1, n ∈ N and n < 5}
y = 2n – 1
when n = 1, y = 2 × 1 – 1
⇒ y = 2 – 1 = 1
when n = 2, y = 2 × 2 – 1
⇒ y = 4 – 1 = 3
when n = 3, y = 2 × 3 – 1
⇒ y = 6 – 1 = 5
when n = 4, y = 2 × 4 – 1
⇒ y = 8 – 1 = 7
∴ N = {1, 3, 5, 7}
Now we see that elements of sets M and N are not the same (identical).
∴ Sets M and N are not equal.
(iii) E = {x : x2 + 8x – 9 = 0}
x2 + 8x – 9 = 0
⇒ x2 + 9x – x – 9 = 0
⇒ x(x + 9) – 1(x + 9) = 0
⇒ (x – 1)(x + 9) = 0
∴ Either x + 9 = 0 or x – 1 = 0
⇒ x = - 9 or x = 1
∴ E = {-9, 1}
F = {1, -9}
Now we see that elements of sets E and F are the same (identical).
∴ Sets E and F are equal.
(iv) A = {x : x ∈ N, x < 3}
= {1, 2}
B = {y : y2 - 3y + 2 = 0}
y2 - 3y + 2 = 0
⇒ y2 - 3y + 2 = 0
⇒ y2 - 2y - y + 2 = 0
⇒ y(y - 2) - 1(y - 2) = 0
⇒ (y - 2)(y - 1) = 0
∴ Either y - 2 = 0 or y - 1 = 0
⇒ y = 2 or y = 1
∴ B = (1, 2}
Now we see that elements of sets A and B are the same (identical).
∴ Sets A and B are equal.
9. State whether each of the following sets is a finite set or an infinite set:
(i) The set of multiples of 8.
(ii) The set of integers less than 10.
(iii) The set of whole numbers less than 12.
(iv) {x : x = 3n – 2, n ∈ W, n ≤ 8}
(v) {x : x = 3n – 2n, n ∈ Z, n ≤ 8}
(vi) {x : x = (n – 2)/(n + 1), n ∈ W)
Solution
(i) The set of multiples of 8
= {8, 16, 24, 32, ….}
It is an infinite set.
(ii) The set of integers less than 10
= {9, 8, 7, 6, 5, 4, 3, 2, 1, -1, -2, …..}
It is an infinite set.
(iii) The set of whole numbers less than 12
= {11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1. 0}
It is a finite set.
(iv) {x : x = 3n – 2, n ∈ W, n ≤ 8}
Substituting the value of n = (0, 1, 2, 3, 4, 5, 6, 7 and 8) we get
= {-2, 1, 4, 7, 10, 13, 16, 19, 22}
It is finite set.
(v) {x : x = 3n – 2, n ∈ Z, n ≤ 8}
= {22, 19, 16, 13, 10, 7, 4, 1, -2, -5, ……}
It is infinite set.
(vi) {x : x = (n – 2)/(n + 1), n ∈ W}
{-2, -1/2, 0, ¼, 2/5 ……….}
It is infinite set.
10. Answer, whether the following statements are true or false. Give reasons.
(i) The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets.
(ii) If E = {factors of 16} and F = {factors of 20}, then E = F.
(iii) The set A = {integers less than 20} is a finite set.
(iv) If A = {x : x is an even prime number}, then set A is empty.
(v) The set of odd prime numbers is the empty set.
(vi) The set of squares of integers and the set of whole numbers are equal sets.
(vii) In n(P) = n(M), then P → M.
(viii) If set P = set M, then n(P) = n(M).
(ix) n(A) = n(B) ⇒ A = B.
Solution
(i) Set of even natural number less than 21
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
∴ Cardinal Number of this set = 10
Set of odd natural numbers less than 21
= {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
∴ Cardinal number of this set = 10
Now we see that cardinal numbers of both these sets = 10
∴ “The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets”…… is a True statement.
(ii) E = {Factors of 16} = {1, 2, 4, 8, 16}
F = {Factors of 20}={1, 2, 4, 5, 10, 20}
Now we see that elements of set E and set F are not the same (identical)
∴ “If E = {Factors of 16} and F = {Factors of 20},
Then, E = F” ……. is a False statement.
(iii) A = {Integers less than 20}
= {19, 18, 17, 16,…0, -1, -2, -3, ….}
∴ “The set A = {Integers less than 20} is a finite set"……is a False statement.
(iv) A = {x : x is an even prime number} = {2}
∴ “If A = {x : x is an even prime number}, then set A is empty”…. is a false statement .
(v) Set of odd prime numbers = {3, 5, 7, 11, 13, 17, 19, 23, …….}
∴ “The set of odd prime number is the empty set”…… is a False statement.
F = {1, -9}
Now we see that elements of sets E and F are the same (identical).
∴ Sets E and F are equal.
(iv) A = {x : x ∈ N, x < 3}
= {1, 2}
B = {y : y2 - 3y + 2 = 0}
y2 - 3y + 2 = 0
⇒ y2 - 3y + 2 = 0
⇒ y2 - 2y - y + 2 = 0
⇒ y(y - 2) - 1(y - 2) = 0
⇒ (y - 2)(y - 1) = 0
∴ Either y - 2 = 0 or y - 1 = 0
⇒ y = 2 or y = 1
∴ B = (1, 2}
Now we see that elements of sets A and B are the same (identical).
∴ Sets A and B are equal.
9. State whether each of the following sets is a finite set or an infinite set:
(i) The set of multiples of 8.
(ii) The set of integers less than 10.
(iii) The set of whole numbers less than 12.
(iv) {x : x = 3n – 2, n ∈ W, n ≤ 8}
(v) {x : x = 3n – 2n, n ∈ Z, n ≤ 8}
(vi) {x : x = (n – 2)/(n + 1), n ∈ W)
Solution
(i) The set of multiples of 8
= {8, 16, 24, 32, ….}
It is an infinite set.
(ii) The set of integers less than 10
= {9, 8, 7, 6, 5, 4, 3, 2, 1, -1, -2, …..}
It is an infinite set.
(iii) The set of whole numbers less than 12
= {11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1. 0}
It is a finite set.
(iv) {x : x = 3n – 2, n ∈ W, n ≤ 8}
Substituting the value of n = (0, 1, 2, 3, 4, 5, 6, 7 and 8) we get
= {-2, 1, 4, 7, 10, 13, 16, 19, 22}
It is finite set.
(v) {x : x = 3n – 2, n ∈ Z, n ≤ 8}
= {22, 19, 16, 13, 10, 7, 4, 1, -2, -5, ……}
It is infinite set.
(vi) {x : x = (n – 2)/(n + 1), n ∈ W}
{-2, -1/2, 0, ¼, 2/5 ……….}
It is infinite set.
10. Answer, whether the following statements are true or false. Give reasons.
(i) The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets.
(ii) If E = {factors of 16} and F = {factors of 20}, then E = F.
(iii) The set A = {integers less than 20} is a finite set.
(iv) If A = {x : x is an even prime number}, then set A is empty.
(v) The set of odd prime numbers is the empty set.
(vi) The set of squares of integers and the set of whole numbers are equal sets.
(vii) In n(P) = n(M), then P → M.
(viii) If set P = set M, then n(P) = n(M).
(ix) n(A) = n(B) ⇒ A = B.
Solution
(i) Set of even natural number less than 21
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
∴ Cardinal Number of this set = 10
Set of odd natural numbers less than 21
= {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
∴ Cardinal number of this set = 10
Now we see that cardinal numbers of both these sets = 10
∴ “The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets”…… is a True statement.
(ii) E = {Factors of 16} = {1, 2, 4, 8, 16}
F = {Factors of 20}={1, 2, 4, 5, 10, 20}
Now we see that elements of set E and set F are not the same (identical)
∴ “If E = {Factors of 16} and F = {Factors of 20},
Then, E = F” ……. is a False statement.
(iii) A = {Integers less than 20}
= {19, 18, 17, 16,…0, -1, -2, -3, ….}
∴ “The set A = {Integers less than 20} is a finite set"……is a False statement.
(iv) A = {x : x is an even prime number} = {2}
∴ “If A = {x : x is an even prime number}, then set A is empty”…. is a false statement .
(v) Set of odd prime numbers = {3, 5, 7, 11, 13, 17, 19, 23, …….}
∴ “The set of odd prime number is the empty set”…… is a False statement.
(vi) Integer Square of Integer Whole No.
∴ Set of squares of integers = {0, 1, 4, 9, 16, 25,…..}
Set of whole numbers = {0, 1, 2, 3, 4, 5, 6, 7,……}
Hence, “The set of squares of integers and the set of whole numbers are equal….. False statement.
(vii) n(P) = n(M)
It means number of elements of set P = Number of elements of set M.
∴ Sets P and M are equivalent.
∴ “If n(P) =⊇ n(M), then P ↔️ M” …… is a true Statement.
(viii) Set P = Set M
It means sets P and M are equal. Equal sets are equivalent also.
∴ Number of elements of set P = Number of elements of set M
∴ “ If set P = set M, then n(P) = n(M)”…….is a True statement.
(ix) n(A) = n(B)
⇒ Number of elements of set A = Number of elements of set B
∴ Given sets are equivalent but not equal.
∴ “ n(A) = n(B) ⇒ A = B” is a False statement.
∴ Set of squares of integers = {0, 1, 4, 9, 16, 25,…..}
Set of whole numbers = {0, 1, 2, 3, 4, 5, 6, 7,……}
Hence, “The set of squares of integers and the set of whole numbers are equal….. False statement.
(vii) n(P) = n(M)
It means number of elements of set P = Number of elements of set M.
∴ Sets P and M are equivalent.
∴ “If n(P) =⊇ n(M), then P ↔️ M” …… is a true Statement.
(viii) Set P = Set M
It means sets P and M are equal. Equal sets are equivalent also.
∴ Number of elements of set P = Number of elements of set M
∴ “ If set P = set M, then n(P) = n(M)”…….is a True statement.
(ix) n(A) = n(B)
⇒ Number of elements of set A = Number of elements of set B
∴ Given sets are equivalent but not equal.
∴ “ n(A) = n(B) ⇒ A = B” is a False statement.
Exercise 6 C
1. Find all the subsets of each of the following sets:
(i) A= {5, 7}
(ii) B = {a, b, c}
(iii) C = {x : x ∈ W, x ≤2}
(iv) {p : p is a letter in the word ‘poor’}
Solution
(i) A = {5, 7}
Subsets of set A = { }, {5}, {7}, {5, 7}
(i) A= {5, 7}
(ii) B = {a, b, c}
(iii) C = {x : x ∈ W, x ≤2}
(iv) {p : p is a letter in the word ‘poor’}
Solution
(i) A = {5, 7}
Subsets of set A = { }, {5}, {7}, {5, 7}
(ii) B = {a, b, c}
Subsets of set B = { }, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}
Subsets of set B = { }, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}
(iii) C = {x : x ∈ W, x ≤ 2}
= {0, 1, 2}
∴ Subsets of set C = ɸ, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}
= {0, 1, 2}
∴ Subsets of set C = ɸ, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}
(iv) {P : P is a letter in the word ‘POOR’} = {p, o, r}
∴ Subsets of the given set = ɸ, {p}, {o}, {r}, {p, o}, {p, r}, {o, r}, {p, o, r}
2. If C is the set of letters in the word “cooler”, find:
(i) Set C
(ii) n(C)
(iii) Number of its subsets
(iv) Number of its proper subsets.
Note : (i) If a set has n elements, the number of its subsets = 2n
(ii) If a set has n elements, the number of its proper subsets = 2n - 1
Solution
(i) C = {c, o, l, e, r}
(ii) n(C) = 5
(iii) Number of its subsets : 25 = 2 × 2 × 2 × 2 × 2 = 32
(iv) Number of its proper subsets = 25 – 1 = 32 – 1 = 31
3. If T = {x: x is a letter in the word ‘TEETH’}, find all its subsets.
Solution
T = {t, e, h}
Subsets of set T = ɸ, {r}, {e}, {h}, {t, e}, {t, h}, {e, h}, {t, e, h}
∴ Subsets of the given set = ɸ, {p}, {o}, {r}, {p, o}, {p, r}, {o, r}, {p, o, r}
2. If C is the set of letters in the word “cooler”, find:
(i) Set C
(ii) n(C)
(iii) Number of its subsets
(iv) Number of its proper subsets.
Note : (i) If a set has n elements, the number of its subsets = 2n
(ii) If a set has n elements, the number of its proper subsets = 2n - 1
Solution
(i) C = {c, o, l, e, r}
(ii) n(C) = 5
(iii) Number of its subsets : 25 = 2 × 2 × 2 × 2 × 2 = 32
(iv) Number of its proper subsets = 25 – 1 = 32 – 1 = 31
3. If T = {x: x is a letter in the word ‘TEETH’}, find all its subsets.
Solution
T = {t, e, h}
Subsets of set T = ɸ, {r}, {e}, {h}, {t, e}, {t, h}, {e, h}, {t, e, h}
4. Given the universal set = {-7, -3, -1, 0, 5, 6, 8, 9}, find:
(i) A = {x : x < 2}
(ii) B = {x : -4 < x < 6}
Solution
Universal set = {-7, -3, -1, 0, 5, 6, 8, 9},
(i) A = {x : x < 2} = {-7, -3, -1, 0}
(ii) B {x : -4 < x < 6} = {-3, -1, 0, 5}
5. Given the universal set = {x : x ∈ N and x < 20}, find:
(i) A = {x : x = 3p; p ∈ N}
(ii) B = {y : y – 2n + 3, n ∈ N}
(iii) C = {x : x is divisible by 4}
Solution
Universal set = {x : x ∈ N and x < 20}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …, 19}
(i) A = {x : x = 3p; p ∈ N}
x = 3p
when p = 1, x = 3 × 1 = 3
when p = 2, x = 3 × 2 = 6
when p = 3, x = 3 × 3 = 9
when p = 4, x = 3 × 4 = 12
when p = 5, x = 3 × 5 = 15
when p = 6, x = 3 × 6 = 18
∴ A = {3, 6, 9, 12, 15, 18)
(ii) B = {y : y = 2n + 3, n ∈ N}
y = 2n + 3
6. Find the proper subsets of {x : x2 – 9x – 10 = 0}
Solution
x2 - 9x – 10 = 0
⇒ x2 – 10x + x – 10 = 0
⇒ x(x – 10) + 1(x – 10) = 0
⇒ (x – 10)(x + 1) = 0
∴ Either x – 10 =0 or x + 1 = 0
x = 10
⇒ x = -1
Given set = {-1, 10}
Proper subsets of this set = ɸ, {-1}, {10}
7. Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}.
State whether the following are true or false. Give reasons.
(i) A ⊂ B
(ii) B ⊆ A
(iii) C ⊆ B
(iv) B ⊂A
(v) C ⊂ A
(vi) C ⊆ B ⊆ A
Solution
(i) A = {x : x < 2}
(ii) B = {x : -4 < x < 6}
Solution
Universal set = {-7, -3, -1, 0, 5, 6, 8, 9},
(i) A = {x : x < 2} = {-7, -3, -1, 0}
(ii) B {x : -4 < x < 6} = {-3, -1, 0, 5}
5. Given the universal set = {x : x ∈ N and x < 20}, find:
(i) A = {x : x = 3p; p ∈ N}
(ii) B = {y : y – 2n + 3, n ∈ N}
(iii) C = {x : x is divisible by 4}
Solution
Universal set = {x : x ∈ N and x < 20}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …, 19}
(i) A = {x : x = 3p; p ∈ N}
x = 3p
when p = 1, x = 3 × 1 = 3
when p = 2, x = 3 × 2 = 6
when p = 3, x = 3 × 3 = 9
when p = 4, x = 3 × 4 = 12
when p = 5, x = 3 × 5 = 15
when p = 6, x = 3 × 6 = 18
∴ A = {3, 6, 9, 12, 15, 18)
(ii) B = {y : y = 2n + 3, n ∈ N}
y = 2n + 3
6. Find the proper subsets of {x : x2 – 9x – 10 = 0}
Solution
x2 - 9x – 10 = 0
⇒ x2 – 10x + x – 10 = 0
⇒ x(x – 10) + 1(x – 10) = 0
⇒ (x – 10)(x + 1) = 0
∴ Either x – 10 =0 or x + 1 = 0
x = 10
⇒ x = -1
Given set = {-1, 10}
Proper subsets of this set = ɸ, {-1}, {10}
7. Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}.
State whether the following are true or false. Give reasons.
(i) A ⊂ B
(ii) B ⊆ A
(iii) C ⊆ B
(iv) B ⊂A
(v) C ⊂ A
(vi) C ⊆ B ⊆ A
Solution
A = {Triangles}
B = {Isosceles triangles}
C = {Equilateral triangles}
(i) False
B = {Isosceles triangles}
C = {Equilateral triangles}
(i) False
Since each triangle is not isosceles.
∴ A ⊂ B,
∴ A ⊂ B,
(ii) True
B ⊆ A
∵ Isosceles Δ is one of the triangles.
(iii) True
Since each equilateral triangle is isosceles also,
∴ C ⊆ B
(iv) True
B ⊂ A
∵ Isosceles Δ is one of the triangles.
(v) True
C ⊂ A
∵ Equilateral Δ is one of the triangles.
(vi) True
C ⊆ B ⊆ A
∵ Each equilateral triangle is isosceles also and each isosceles Δ is a form of triangles.
8. Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D = {rhombuses}. State, giving reasons, whether the following are true or false.
(i) B ⊂ C
(ii) D ⊂ B
(iii) C ⊆ B ⊆ A
(iv) D ⊂ A
(v) B ⊇ C
(vi) A ⊇ B ⊇ D
Solution
A = {Quadrilaterals}
B = {Rectangles}
C = {Square}
D = {Rhombuses}
(i) B ⊂ C
(ii) D ⊂ B
(iii) C ⊆ B ⊆ A
(iv) D ⊂ A
(v) B ⊇ C
(vi) A ⊇ B ⊇ D
Solution
A = {Quadrilaterals}
B = {Rectangles}
C = {Square}
D = {Rhombuses}
(i) False
B ⊂ C
∵ Rectangle is not a square also.
(ii) False
D ⊂ B
∵ Rhombus is not a rectangle also.
(iii) True
C ⊆ B ⊆ A
∵ Every square is a rectangle also and every rectangle is a quadrilateral also
(iv) True
D ⊂ A
∵ Rhombus is one of the quadrilaterals.
(v) True
B ⊇ C
∵ Square is a rectangle also.
(vi) False
A ⊇ B ⊇ D
∵ Rhombus is not a rectangle also.
9. Given, universal set = {x : x ∈ N, 10 ≤ x ≤ 35}.
A = {x ∈ N: x ≤ 16} and
B = {x : x > 29} Find:
(i) A’
(ii) B’
Solution
Universal set = {x : x ∈ N, 10 ≤ x ≤ 35}
= {10, 11, 12, 13, 14, 15, ….34, 35}
A = {x ∈ N : x ≤ 16}
= {10, 11, 12, 13, 14, 15, 16}
B = {x : x > 29}
= {30, 31, 32, 33, 34, 35}
∵ Rhombus is not a rectangle also.
9. Given, universal set = {x : x ∈ N, 10 ≤ x ≤ 35}.
A = {x ∈ N: x ≤ 16} and
B = {x : x > 29} Find:
(i) A’
(ii) B’
Solution
Universal set = {x : x ∈ N, 10 ≤ x ≤ 35}
= {10, 11, 12, 13, 14, 15, ….34, 35}
A = {x ∈ N : x ≤ 16}
= {10, 11, 12, 13, 14, 15, 16}
B = {x : x > 29}
= {30, 31, 32, 33, 34, 35}
(i) A’ = {17, 18, 19, 20, 21, 22,….,33, 34, 35}
= {x : x ∈ N; 17 ≤ x ≤ 35}
= {x : x ∈ N; 17 ≤ x ≤ 35}
(ii) B’ = {10, 11, 12, 13, 14, 15, …., 29}
= {x : x ≤ 29}
10. Given universal set = {x ∈ Z : -6 < x ≤ 6}, N = {n : n is a non – negative number} and
P = {x : x is a non-positive number}
Find : (i) N’
(ii) P’
Solution
Universal set = {x ∈ Z; - 6 < x ≤ 6}
= {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
N = {n : n is a non-negative number}
= {0, 1, 2, 3, 4, 5, 6}
P = {x : x is a non-positive number}
= {-5, -4, -3, -2, -1, 0}
(i) N' = {-5, -4, -3, -2, -1}
(ii) P’ = {1, 2, 3, 4, 5, 6}
11. Let M = {letters of the word REAL} and N = {letters of the word LARE}. Write sets M and N in roster form and then state whether;
(i) M ⊆ N is true
(ii) N ⊆ M is true.
(iii) M = N is true.
Solution
M = {letters of the word REAL]
= {R, E, A, L}
And N = {letters of the word LARE}
= {L, A, R, E}
(i) M ⊆ N is true: yes
(ii) N ⊆ M is true.
(iii) M = N is true.
12. Write two sets A and B such that A ⊆ B and B ⊆ A. State the relationship between set A and B.
Solution
Let A = {letters of TALE}
B = {Letters of LATE}
Here A ⊆ B, B ⊆ A
∴ A = B
= {x : x ≤ 29}
10. Given universal set = {x ∈ Z : -6 < x ≤ 6}, N = {n : n is a non – negative number} and
P = {x : x is a non-positive number}
Find : (i) N’
(ii) P’
Solution
Universal set = {x ∈ Z; - 6 < x ≤ 6}
= {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
N = {n : n is a non-negative number}
= {0, 1, 2, 3, 4, 5, 6}
P = {x : x is a non-positive number}
= {-5, -4, -3, -2, -1, 0}
(i) N' = {-5, -4, -3, -2, -1}
(ii) P’ = {1, 2, 3, 4, 5, 6}
11. Let M = {letters of the word REAL} and N = {letters of the word LARE}. Write sets M and N in roster form and then state whether;
(i) M ⊆ N is true
(ii) N ⊆ M is true.
(iii) M = N is true.
Solution
M = {letters of the word REAL]
= {R, E, A, L}
And N = {letters of the word LARE}
= {L, A, R, E}
(i) M ⊆ N is true: yes
(ii) N ⊆ M is true.
(iii) M = N is true.
12. Write two sets A and B such that A ⊆ B and B ⊆ A. State the relationship between set A and B.
Solution
Let A = {letters of TALE}
B = {Letters of LATE}
Here A ⊆ B, B ⊆ A
∴ A = B
Exercise 6 D
1. Given A = {x : x ∈ N and 3 < x ≤ 6} and B = {x : ∈ W and x < 4}. Find :
(i) Sets A and B in roster form
(ii) A ⋃ B
(iii) A ⋂ B.
(iv) A – B
(v) B – A
Solution
(i) A = (4, 5, 6)
B = (0, 1, 2, 3)
(ii) A⋃ B = {0, 1, 2, 3, 4, 5, 6}
(iii) A ⋂ B = (ɸ)
(iv) A – B = (4, 5, 6)
(v) B – A = (0, 1, 2, 3)
2. If P = {x : x ∈ W and 4 ≤ x ≤ 8}, and Q = { x : x ∈ N and x < 6}. Find:
(i) P⋃ Q and P ⋂ Q.
(ii) Is (P ⋃ Q) ⊃ (P ⋂ Q)?
Solution
(i) P = (4, 5, 6, 7, 8)
Q = (1, 2, 3, 4, 5)
P ⋃ Q = (1, 2, 3, 4, 5, 6, 7, 8)
P ⋂ Q = (4, 5)
(i) Sets A and B in roster form
(ii) A ⋃ B
(iii) A ⋂ B.
(iv) A – B
(v) B – A
Solution
(i) A = (4, 5, 6)
B = (0, 1, 2, 3)
(ii) A⋃ B = {0, 1, 2, 3, 4, 5, 6}
(iii) A ⋂ B = (ɸ)
(iv) A – B = (4, 5, 6)
(v) B – A = (0, 1, 2, 3)
2. If P = {x : x ∈ W and 4 ≤ x ≤ 8}, and Q = { x : x ∈ N and x < 6}. Find:
(i) P⋃ Q and P ⋂ Q.
(ii) Is (P ⋃ Q) ⊃ (P ⋂ Q)?
Solution
(i) P = (4, 5, 6, 7, 8)
Q = (1, 2, 3, 4, 5)
P ⋃ Q = (1, 2, 3, 4, 5, 6, 7, 8)
P ⋂ Q = (4, 5)
(ii) Yes, all the element of set P ⋃ Q are contained in the set P ⋂ Q. Therefore, P ⋃ Q is a proper sunset of P ⋂ Q.
3. If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W) and C = {x : x ≤ 5 and x ∈ N}. Find:
(i) A ⋃ B and (A ⋃ B) ⋃ C
(ii) B ⋃ C and A ⋃ (B ⋃ C)
(iii) A ⋂ B and (A ⋂ B) ⋂ C
(iv) B ⋂ C and A ⋂ (B ⋂ C)
Is (A ⋃ B) ⋃ C = A ⋃ (B ⋃ C)?
Is (A ⋂ B) ⋂ C = A ⋂ (B ⋂ C)?
Solution
A = (5, 6, 7, 8, 9)
B = (4, 5, 6, 7)
C = (1, 2, 3, 4, 5)
(i) A ⋃ B = (4, 5, 6, 7, 8, 9)
(A ⋃ B) ⋃ C = (1, 2, 3, 4, 5, 6, 7, 8, 9)
(ii) B ⋃ C (1, 2, 3, 4, 5, 6, 7)
A ⋃ (B ⋃ C) = (1, 2, 3, 4, 5, 6, 7, 8, 9)
(iii) A ⋂ B = (5, 6, 7)
(A ⋂ B) ⋂ C = (5)
(iv) B ⋂ C = (4, 5)
A ⋂ (B ⋂ C) = (5)
(v) (A ⋃ B) ⋃ C = (1, 2, 3, 4, 5, 6, 7, 8, 9)
A ⋃ (B ⋃ C) = (1, 2, 3, 4, 5, 6, 7, 8, 9)
Yes, these are equal.
(vi) (A ⋂ B) ⋂ C = A ⋂ (B ⋂ C)
{5} = {5}
Yes, these are equal.
4. Given A = {0, 1, 2, 4, 5}
B = {0, 2, 4, 6, 8} and C = {0, 3, 6, 9}. Show that
(i) A ⋃ (B ⋃ C) = (A ⋃ B) ⋃ C i. e., the union of sets is associative.
(ii) A ⋂ (B ⋂ C) = (A ⋂ B) ⋂ C i.e., the intersection of sets is associative.
Solution
A = {0, 1, 2, 4, 5}
B = {0, 2, 4, 6, 8}
C = {0, 3, 6, 9}
(i) B ⋃ C = {0, 2, 4, 6, 8} ⋃ {0, 3, 6, 9}
= {0, 2, 3, 4, 6, 8, 9}
∴ A ⋃ (B ⋃ C) = {0, 1, 2, 4, 5} ⋃ {0, 2, 3, 4, 6, 8, 9}
⇒ A ⋃ (B ⋃ C) = {0, 1, 2, 3, 4, 5, 6, 8, 9} ...(i)
A ⋃ B = {0, 1, 2, 4, 5} ⋃ {0, 2, 4, 6, 8}
= {0, 1, 2, 4, 5, 6, 8}
∴ (A ⋃ B) ⋃ C = {0, 1, 2, 4, 5, 6, 8} ⋃ {0, 3, 6, 9}
⇒ (A ⋃ B) ⋃ C = {0, 1, 2, 3, 4, 5, 6, 8, 9} ...(ii)
From I and II, we get
A ⋃ (B ⋃ C) = A ⋃ (B ⋃ C)
(ii) B ⋂ C = {0, 2, 4, 6, 8} ⋂ {0, 3, 6, 9}
= {0, 6}
Now, A ⋂ (B ⋂ C) = {1, 2, 4, 5} ⋂ {0, 6}
⇒ A ⋂ (B ⋂ C) = {0} …(i)
A ⋂ B = {0, 1, 2, 4, 5} ⋂ {0, 2, 4, 6, 8}
= {0, 2, 4}
∴ (A ⋂ B) ⋂ C = {0, 2, 4} ⋂ {0, 3, 6, 9}
⇒ A ⋂ (B ⋂ C) = {0} …(ii)
From I and II we get
A ⋂ (B ⋂ C) = (A ⋂ B) ⋂ C
3. If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W) and C = {x : x ≤ 5 and x ∈ N}. Find:
(i) A ⋃ B and (A ⋃ B) ⋃ C
(ii) B ⋃ C and A ⋃ (B ⋃ C)
(iii) A ⋂ B and (A ⋂ B) ⋂ C
(iv) B ⋂ C and A ⋂ (B ⋂ C)
Is (A ⋃ B) ⋃ C = A ⋃ (B ⋃ C)?
Is (A ⋂ B) ⋂ C = A ⋂ (B ⋂ C)?
Solution
A = (5, 6, 7, 8, 9)
B = (4, 5, 6, 7)
C = (1, 2, 3, 4, 5)
(i) A ⋃ B = (4, 5, 6, 7, 8, 9)
(A ⋃ B) ⋃ C = (1, 2, 3, 4, 5, 6, 7, 8, 9)
(ii) B ⋃ C (1, 2, 3, 4, 5, 6, 7)
A ⋃ (B ⋃ C) = (1, 2, 3, 4, 5, 6, 7, 8, 9)
(iii) A ⋂ B = (5, 6, 7)
(A ⋂ B) ⋂ C = (5)
(iv) B ⋂ C = (4, 5)
A ⋂ (B ⋂ C) = (5)
(v) (A ⋃ B) ⋃ C = (1, 2, 3, 4, 5, 6, 7, 8, 9)
A ⋃ (B ⋃ C) = (1, 2, 3, 4, 5, 6, 7, 8, 9)
Yes, these are equal.
(vi) (A ⋂ B) ⋂ C = A ⋂ (B ⋂ C)
{5} = {5}
Yes, these are equal.
4. Given A = {0, 1, 2, 4, 5}
B = {0, 2, 4, 6, 8} and C = {0, 3, 6, 9}. Show that
(i) A ⋃ (B ⋃ C) = (A ⋃ B) ⋃ C i. e., the union of sets is associative.
(ii) A ⋂ (B ⋂ C) = (A ⋂ B) ⋂ C i.e., the intersection of sets is associative.
Solution
A = {0, 1, 2, 4, 5}
B = {0, 2, 4, 6, 8}
C = {0, 3, 6, 9}
(i) B ⋃ C = {0, 2, 4, 6, 8} ⋃ {0, 3, 6, 9}
= {0, 2, 3, 4, 6, 8, 9}
∴ A ⋃ (B ⋃ C) = {0, 1, 2, 4, 5} ⋃ {0, 2, 3, 4, 6, 8, 9}
⇒ A ⋃ (B ⋃ C) = {0, 1, 2, 3, 4, 5, 6, 8, 9} ...(i)
A ⋃ B = {0, 1, 2, 4, 5} ⋃ {0, 2, 4, 6, 8}
= {0, 1, 2, 4, 5, 6, 8}
∴ (A ⋃ B) ⋃ C = {0, 1, 2, 4, 5, 6, 8} ⋃ {0, 3, 6, 9}
⇒ (A ⋃ B) ⋃ C = {0, 1, 2, 3, 4, 5, 6, 8, 9} ...(ii)
From I and II, we get
A ⋃ (B ⋃ C) = A ⋃ (B ⋃ C)
(ii) B ⋂ C = {0, 2, 4, 6, 8} ⋂ {0, 3, 6, 9}
= {0, 6}
Now, A ⋂ (B ⋂ C) = {1, 2, 4, 5} ⋂ {0, 6}
⇒ A ⋂ (B ⋂ C) = {0} …(i)
A ⋂ B = {0, 1, 2, 4, 5} ⋂ {0, 2, 4, 6, 8}
= {0, 2, 4}
∴ (A ⋂ B) ⋂ C = {0, 2, 4} ⋂ {0, 3, 6, 9}
⇒ A ⋂ (B ⋂ C) = {0} …(ii)
From I and II we get
A ⋂ (B ⋂ C) = (A ⋂ B) ⋂ C
5. If A = {x ∈ W : 5 < x < 10}, B = {3, 4, 5, 6, 7} and C = {x = 2n ; x ∈ N and n ≤ 4}. Find:
(i) A ⋂ (B ⋃ C)
(ii) (B ⋃ A) ⋂ (B ⋃ C)
(iii) B ⋃ (A ⋂ C)
(iv) (A ⋂ B) ⋃ (A ⋂ C)
Name the sets which are equal.
Solution
A = {x ∈ W ; 5 < x < 10}
= {6, 7, 8, 9}
B = {3, 4, 5, 6, 7}
C = {x = 2n ; n ∈ N and n ≤ 4}
x = 2n
when n = 1, x = 2 × 1= 2
when n = 2, x = 2 × 2 = 4
when n = 3, x = 2 × 3 = 6
when n = 4, x = 2 × 4 = 8
∴ C = {2, 4, 6, 8}
(i) A ⋂ (B ⋃ C)
(ii) (B ⋃ A) ⋂ (B ⋃ C)
(iii) B ⋃ (A ⋂ C)
(iv) (A ⋂ B) ⋃ (A ⋂ C)
Name the sets which are equal.
Solution
A = {x ∈ W ; 5 < x < 10}
= {6, 7, 8, 9}
B = {3, 4, 5, 6, 7}
C = {x = 2n ; n ∈ N and n ≤ 4}
x = 2n
when n = 1, x = 2 × 1= 2
when n = 2, x = 2 × 2 = 4
when n = 3, x = 2 × 3 = 6
when n = 4, x = 2 × 4 = 8
∴ C = {2, 4, 6, 8}
(i) B ⋃ C = {3, 4, 5, 6, 7} ⋃ {2, 4, 6, 8}
= {2, 3, 4, 5, 6, 7, 8}
A ⋂ (B ⋃ C) = {6, 7, 8, 9} ⋂ {2, 3, 4, 5, 6, 7, 8}
⇒ A ⋂ (B ⋃ C) = {6, 7, 8}
(ii) B ⋃ A = {3, 4, 5, 6, 7} ⋃ {6, 7, 8, 9}
= {3, 4, 5, 6, 7, 8, 9}
(B ⋃ A) ⋃ (B ⋃ C)
= {3, 4, 5, 6, 7, 8, 9} ⋂ {2, 3, 4, 5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}
(iii) (A ⋂ C) = {6, 7, 8, 9} ⋂ {2, 4, 6, 8}
= {6, 8}
B ⋃ (A ⋂ C) = {3, 4, 5, 6, 7} ⋃ {6, 8}
= {3, 4, 5, 6, 7, 8}
(iv) (A ⋃ B) = {6, 7, 8, 9} ⋂ {3, 4, 5, 6, 7}
= {6, 7}
∴ (A ⋂ B) ⋃ (A ⋂ C) = {6, 7} ⋃ {6, 8}
= {6, 7, 8}
6. If P = {factors of 36} and Q = {factors of 48}; find:
(i) P ⋃ Q
(ii) P ⋂ Q
(iii) Q – P
(iv) P’ ⋂ Q
Solution
1 × 36 = 36, 1 × 48 = 48
2 × 18 = 36, 2 × 24 = 48
3 × 12 = 36, 3 × 16 = 48
4 × 9 = 36, 4 × 12 = 48
6 × 6 = 36, 6 × 8 = 48
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
P = {factors of 36}
= {1,2, 3, 4, 6, 9, 12, 18, 36}
Q = {factors of 48}
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
= {2, 3, 4, 5, 6, 7, 8}
A ⋂ (B ⋃ C) = {6, 7, 8, 9} ⋂ {2, 3, 4, 5, 6, 7, 8}
⇒ A ⋂ (B ⋃ C) = {6, 7, 8}
(ii) B ⋃ A = {3, 4, 5, 6, 7} ⋃ {6, 7, 8, 9}
= {3, 4, 5, 6, 7, 8, 9}
(B ⋃ A) ⋃ (B ⋃ C)
= {3, 4, 5, 6, 7, 8, 9} ⋂ {2, 3, 4, 5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}
(iii) (A ⋂ C) = {6, 7, 8, 9} ⋂ {2, 4, 6, 8}
= {6, 8}
B ⋃ (A ⋂ C) = {3, 4, 5, 6, 7} ⋃ {6, 8}
= {3, 4, 5, 6, 7, 8}
(iv) (A ⋃ B) = {6, 7, 8, 9} ⋂ {3, 4, 5, 6, 7}
= {6, 7}
∴ (A ⋂ B) ⋃ (A ⋂ C) = {6, 7} ⋃ {6, 8}
= {6, 7, 8}
6. If P = {factors of 36} and Q = {factors of 48}; find:
(i) P ⋃ Q
(ii) P ⋂ Q
(iii) Q – P
(iv) P’ ⋂ Q
Solution
1 × 36 = 36, 1 × 48 = 48
2 × 18 = 36, 2 × 24 = 48
3 × 12 = 36, 3 × 16 = 48
4 × 9 = 36, 4 × 12 = 48
6 × 6 = 36, 6 × 8 = 48
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
P = {factors of 36}
= {1,2, 3, 4, 6, 9, 12, 18, 36}
Q = {factors of 48}
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
(i) P ⋃ Q = {1, 2 , 3, 4, 6, 9, 12, 18, 36} ⋃ {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
= {1, 2, 3, 4, 6, 8, 9,12, 16, 18, 24, 36, 48}
(ii) P ⋂ Q = {1, 2, 3, 4, 6, 9, 12, 18, 36} ⋂ {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
= {1, 2, 3, 4, 6, 12}
(iii) Q – P = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} – {1, 2, 3, 4, 6, 9, 12, 18, 36}
= {8, 16, 24, 48}
(iv) P’ ⋂ Q = Only Q
= Q – P
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} – {1, 2, 3, 4, 6, 9, 12, 18, 36}
= {8, 16, 24, 48}
7. If A = {6, 7, 8, 9}, B = {4, 6, 8, 10} and C = {x : x ∈ N : 2 < x ≤ 7} find
(i) A – B
(ii) B – C
(iii) B – (A – C)
(iv) A – (B ⋃ C)
(v) B – (A ⋂ C)
(vi) B – B.
Solution
A = [6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
= {1, 2, 3, 4, 6, 8, 9,12, 16, 18, 24, 36, 48}
(ii) P ⋂ Q = {1, 2, 3, 4, 6, 9, 12, 18, 36} ⋂ {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
= {1, 2, 3, 4, 6, 12}
(iii) Q – P = {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} – {1, 2, 3, 4, 6, 9, 12, 18, 36}
= {8, 16, 24, 48}
(iv) P’ ⋂ Q = Only Q
= Q – P
= {1, 2, 3, 4, 6, 8, 12, 16, 24, 48} – {1, 2, 3, 4, 6, 9, 12, 18, 36}
= {8, 16, 24, 48}
7. If A = {6, 7, 8, 9}, B = {4, 6, 8, 10} and C = {x : x ∈ N : 2 < x ≤ 7} find
(i) A – B
(ii) B – C
(iii) B – (A – C)
(iv) A – (B ⋃ C)
(v) B – (A ⋂ C)
(vi) B – B.
Solution
A = [6, 7, 8, 9}
B = {4, 6, 8, 10}
C = {x : x ∈ N : 2 < x ≤ 7}
= {3, 4, 5, 6, 7}
(i) A - B = {6, 7, 8, 9} – {4, 6, 8, 10}
= {7, 9}
(ii) B – C = {4, 6, 8, 10} – {3, 4, 5, 6, 7}
= {8, 10}
(iii) A – C = {6, 7, 8, 9} - {3, 4, 5, 6, 7}
= {8, 9}
B – (A – C) = {4, 6, 8, 10} – {8, 9}
= {4, 6, 10}
(iv) B ⋃ C = {4, 6, 8, 10} ⋃ {3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7, 8, 10}
A – (B ⋃ C) = {6, 7, 8, 9} – {3, 4, 5, 6, 7, 8, 10}
= {9}
(v) A ⋂ C = {6, 7, 8, 9} ⋂ (3, 4, 5, 6, 7}
= {6, 7}
B – (A ⋂ C) = {4, 6, 8, 10} – {6, 7}
= {4, 8, 10}
(vi) B – B = {4, 6, 8, 10} – {4, 6, 8, 10}
= ɸ
8. If A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
and C = {3, 4, 5, 6}
Verify:
(i) A – (B ⋃ C) = (A – B) ⋂ (A – C)
(ii) A – (B ⋂ C) = (A – B) ⋃ (A – C)
Solution
A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
= {7, 9}
(ii) B – C = {4, 6, 8, 10} – {3, 4, 5, 6, 7}
= {8, 10}
(iii) A – C = {6, 7, 8, 9} - {3, 4, 5, 6, 7}
= {8, 9}
B – (A – C) = {4, 6, 8, 10} – {8, 9}
= {4, 6, 10}
(iv) B ⋃ C = {4, 6, 8, 10} ⋃ {3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7, 8, 10}
A – (B ⋃ C) = {6, 7, 8, 9} – {3, 4, 5, 6, 7, 8, 10}
= {9}
(v) A ⋂ C = {6, 7, 8, 9} ⋂ (3, 4, 5, 6, 7}
= {6, 7}
B – (A ⋂ C) = {4, 6, 8, 10} – {6, 7}
= {4, 8, 10}
(vi) B – B = {4, 6, 8, 10} – {4, 6, 8, 10}
= ɸ
8. If A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
and C = {3, 4, 5, 6}
Verify:
(i) A – (B ⋃ C) = (A – B) ⋂ (A – C)
(ii) A – (B ⋂ C) = (A – B) ⋃ (A – C)
Solution
A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
(i) B ⋃ C = {2, 4, 6, 8} ⋃ {3, 4, 5, 6}
= {2, 3, 4, 5, 6, 8}
A – (B ⋃ C) = {1, 2, 3, 4, 5} – {2, 3, 4, 5, 6, 8}
= {1}
A – B = {1, 2, 3, 4, 5} – {2, 4, 6, 8}
= {1, 3, 5}
A – C = {1, 2, 3, 4, 5} – {3, 4, 5, 6}
= {1, 2}
∴ (A – B) ⋂ (A – C) = {1, 3, 5} – {1, 2} = {1}
∴ A – (B ⋃ C) = (A – B) ⋂ (A – C)
(ii) B ⋂ C = {2, 4, 6, 8} ⋂ {3, 4, 5, 6}
= {4, 6}
A – (B ⋂ C} = {1, 2, 3, 4, 5} – {4, 6}
= {1, 2, 3, 5}
A – B = {1, 2, 3, 4, 5} – {2, 4, 6, 8}
= {1, 3, 5}
A – C = {1, 2, 3, 4, 5} – {3, 4, 5, 6}
= {1, 2}
(A – B) ⋃ (A – C) = {1, 3, 5} ⋃ {1, 2}
= {1, 2, 3, 5}
∴ A – (B ⋂ C) = (A – B) ⋃ (A – C)
9. Given A = {x ∈ N : x < 6}, B = {3, 6, 9} and C = {x ∈ N : 2x – 5 ≤ 8}.
= {2, 3, 4, 5, 6, 8}
A – (B ⋃ C) = {1, 2, 3, 4, 5} – {2, 3, 4, 5, 6, 8}
= {1}
A – B = {1, 2, 3, 4, 5} – {2, 4, 6, 8}
= {1, 3, 5}
A – C = {1, 2, 3, 4, 5} – {3, 4, 5, 6}
= {1, 2}
∴ (A – B) ⋂ (A – C) = {1, 3, 5} – {1, 2} = {1}
∴ A – (B ⋃ C) = (A – B) ⋂ (A – C)
(ii) B ⋂ C = {2, 4, 6, 8} ⋂ {3, 4, 5, 6}
= {4, 6}
A – (B ⋂ C} = {1, 2, 3, 4, 5} – {4, 6}
= {1, 2, 3, 5}
A – B = {1, 2, 3, 4, 5} – {2, 4, 6, 8}
= {1, 3, 5}
A – C = {1, 2, 3, 4, 5} – {3, 4, 5, 6}
= {1, 2}
(A – B) ⋃ (A – C) = {1, 3, 5} ⋃ {1, 2}
= {1, 2, 3, 5}
∴ A – (B ⋂ C) = (A – B) ⋃ (A – C)
9. Given A = {x ∈ N : x < 6}, B = {3, 6, 9} and C = {x ∈ N : 2x – 5 ≤ 8}.
Show that:
(i) A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)
(ii) A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C)
Solution
A = {x ∈ N : x < 6}
B = {1, 2, 3, 4, 5}
C = {x ∈ N : 2x -5 ≤ 8}
2x – 5 ≤ 8
⇒ 2x ≤ 8 + 5
⇒ 2x ≤ 13
⇒ x ≤ 13/2
⇒ x ≤ 6.5
∴ C = {1, 2, 3, 4, 5, 6}
(i) B ⋂ C = {3, 6, 9} ⋂ {1, 2, 3, 4, 5, 6}
= {3, 6}
∴ A ⋃ (B ⋂ C) = {1, 2, 3, 4, 5} ⋃ {3, 6}
= {1, 2, 3, 4, 5, 6}
A ⋃ B = {1, 2, 3, 4, 5} ⋃ {3, 6, 9}
= {1, 2, 3, 4, 5, 6, 9}
A ⋃ C = {1, 2, 3, 4, 5} ⋃ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
∴ (A ⋃ B) ⋂ (A ⋃ C)
= {1, 2, 3, 4, 5, 6, 9} ⋂ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
∴ A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)
(ii) B ⋃ C = {3, 6, 9} ⋃ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6, 9}
A ⋂ (B ⋃ C) = {1, 2, 3, 4, 5} ⋂ {1, 2, 3, 4, 5, 6, 9}
= {1, 2, 3, 4, 5}
Now A ⋂ C = {1, 2, 3, 4, 5} ⋂ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5}
A ⋂ B = {1, 2, 3, 4, 5} ⋂ {3, 6, 9}
= {3}
∴ (A ⋂ B) ⋃ (A ⋂ C) = {3} ⋃ {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
∴ A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C)
(i) A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)
(ii) A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C)
Solution
A = {x ∈ N : x < 6}
B = {1, 2, 3, 4, 5}
C = {x ∈ N : 2x -5 ≤ 8}
2x – 5 ≤ 8
⇒ 2x ≤ 8 + 5
⇒ 2x ≤ 13
⇒ x ≤ 13/2
⇒ x ≤ 6.5
∴ C = {1, 2, 3, 4, 5, 6}
(i) B ⋂ C = {3, 6, 9} ⋂ {1, 2, 3, 4, 5, 6}
= {3, 6}
∴ A ⋃ (B ⋂ C) = {1, 2, 3, 4, 5} ⋃ {3, 6}
= {1, 2, 3, 4, 5, 6}
A ⋃ B = {1, 2, 3, 4, 5} ⋃ {3, 6, 9}
= {1, 2, 3, 4, 5, 6, 9}
A ⋃ C = {1, 2, 3, 4, 5} ⋃ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
∴ (A ⋃ B) ⋂ (A ⋃ C)
= {1, 2, 3, 4, 5, 6, 9} ⋂ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
∴ A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)
(ii) B ⋃ C = {3, 6, 9} ⋃ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6, 9}
A ⋂ (B ⋃ C) = {1, 2, 3, 4, 5} ⋂ {1, 2, 3, 4, 5, 6, 9}
= {1, 2, 3, 4, 5}
Now A ⋂ C = {1, 2, 3, 4, 5} ⋂ {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5}
A ⋂ B = {1, 2, 3, 4, 5} ⋂ {3, 6, 9}
= {3}
∴ (A ⋂ B) ⋃ (A ⋂ C) = {3} ⋃ {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5}
∴ A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C)
Exercise 6 E
1. From the given diagram find:
(i) A ⋃ B
(ii) A’ ⋂ B
(iii) A – B
(iv) B – A
(v) (A ⋃ B)’
Solution
(i) A ⋃ B= {a, c, d, e} ⋃ {b, c, e, f}
⇒ A ⋃ B = {a, b, c, d, e, f}
(ii) A’ = {b, f, g, h}
A’ ⋂ B = {b, f, g, h} ⋂ {b, c, e, f}
⇒ A’ ⋂ B = {b, f}
(iii) A - B = {a, c, d, e} – {b, c, e, f}
⇒ A – B = {a, d}
(iv) B – A = {b, c, e, f} – {a, c, d, e}
= {b, f}
(v) A ⋃ B = {a, b, c, d, e, f}
∴ (A ⋃ B)’ = {h, g}
2. From the given diagram, find:
(i) A’
(ii) B’
(iii) A’ ⋃ B’
(iv) (A ⋃ B)’
Is A’ ⋃ B’ = (A ⋂ B)’?
Also, verify if A’ ⋂ B’ = (A ⋃ B)’.
Solution
(i) A = {1, 3, 4, 6}
∴ A’ = {2, 5, 7, 8, 9, 10}
(ii) B = {1, 2, 5}
∴ B’ = {3, 4, 6, 7, 8, 9, 10}
(iii) A’ ⋃ B’ = {2, 5, 7, 8, 9, 10} ⋃ {3, 4, 6, 7, 8, 9, 10}
= {2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) A ⋂ B = {1, 3, 4, 6} ⋂ {1, 2, 5}
= {1}
∴ (A ⋂ B)’ = {2, 3, 4, 5, 6, 7, 8, 9, 10}
From part (iii) and part (iv) we conclude
A’ ⋃ B’ = (A ⋂ B)’
Now A ⋂ B = {2, 5, 7, 8, 9, 10} ⋂ {3, 4, 6, 7, 8, 9, 10}
⇒ A’ ⋂ B’ = {7, 8, 9, 10} ...(i)
Now A ⋃ B = {1, 3, 4, 6} ⋃ {1, 2, 5}
= {1, 2, 3 4, 5, 6}
∴ (A ⋃ B’) = {7, 8, 9, 10} …(ii)
From I and II we conclude
A’ ⋃ B’ = (A ⋂ B)’
3. Use the given diagram to find:
(i) A ⋃ (B ⋂ C)
(ii) B – (A – C)
(iii) A – B.
(iv) A ⋂ B’
Is A ⋂ B’ = A – B?
Solution
(i) B ⋂ C = {d, e, f, g, h, j} ⋂ {h, i, j, k, l}
= {h, j}
∴ A ⋃ (B ⋂ C) = {a, b, c, d, g, h, i} ⋃ {h, j}
= {a, b, c, d, g, h, I, j}
(ii) A – C = {a, b, c, d, g, h, i} – {h, i, j, k, l}
= {a, b, c, d, g}
∴ B – (A – C) = {d, e, f, g, h, j} – {a, b, c, d, g}
= {e, f, h, j}
(iii) A – B = {a, b, c, d, g, h, i} – {d, e, f, g, h, i}
⇒ A – B = {a, b, c, i}
(iv) B’ = {a, b, c, i, k, l, m, n, p}
A ⋂ B’= {a, b, c, d, g, h, i} ⋂ {a, b, c, I, k, l, m, n, p}
⇒ A ⋂ B’ = {a, b, c, i} …..II
From I and II we can conclude A ⋂ B’ = A – B
4. Use the given Venn – diagram to find:
(i) B – A
(ii) A
(iii) B’
(iv) A ⋂ B
(v) A ⋃ B
Solution
(i) B – A = {1, 5} – {1, 5, 6, 7, 9}
= { }
(ii) A = {1, 5, 6, 7, 9}
(iii) B = {1, 5}
∴ B’ = {2, 3, 4, 6, 7, 8, 9, 10}
(iv) A ⋃ B = {1, 5, 6, 7, 9} ⋃ {1, 5}
= {1, 5, 6, 7, 9}
5. Draw a Venn – diagram to show the relationship between two overlapping sets A and B. Now shade the region representing:
(i) A ⋂ B
(ii) A ⋃ B
(iii) B – A
Solution
(i) A ⋂ B =
(ii) A ⋃ B =
(iii) B – A =
6. Draw a Venn –diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing:
(i) A ⋃ B
(ii) B’ ⋂ A
(iii) A ⋂ B
(iv) (A ⋃ B)’
Solution
(i) A ⋃ B =
(ii) B’ ⋂ A =
(iii) A ⋂ B =
(iv) (A ⋃ B)’
7. Two set A and B are are such that A ⋂ B = ɸ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing:
(i) A ⋃ B
(ii) (A ⋃ B)’
(iii) B - A
(iv) B ⋂ A’
Solution
(i) A ⋃ B =
(ii) (A ⋃ B)’ =
(iii) B – A
(iv) B ⋂ A’ =
8. State the sets represented by the shaded portion of following venn-diagrams:
(i)
(ii)
(iii)
Solution
(i) (A ⋃ B)’
(ii) B – A or A’ ⋃ B
(iii) (B - A)’
9. In each of the given diagrams, shade the region which represents the set given underneath the diagram:
(i)
(ii)
(iii)
(ii) B – (A ⋂ C)
(iii) (B ⋂ C) ⋃ A
Verify:
A – (B ⋂ C) = (A – B) ⋃ (A – C)
Solution
(i) A ⋃ B = {a, b, c, d} ⋃ {c, d, e, g}
= {a, b, c, d, e, g}
∴ (A ⋃ B) – C = {a, b, c, d, e, g} – {b, c, e, f}
= {a, d, g}
(ii) A ⋂ C = {a, b, c, d} ⋂ {b, c, e, f}
= {b, c}
∴ B – (A ⋂ C) = {c, d, e, g} – {b, c}
= {d, e, g}
(iii) B ⋂ C = {c, e, d, g} ⋂ {b, c, e, f}
= {c, e}
11. Using the given diagram, express the following sets in the terms of A and B.
(i) {a, d}
(ii) {a, d, c, f}
(iii) {a, d, c, f, g, h}
(iv) {a, d, g, h}
(v) {g, h}
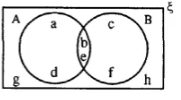Solution
(i) {a, d} = {a, b, e, d} – {b, c, e, f}
= A – B
(ii) {a, d, c, f} = (A ⋃ B) – {b, e}
= (A ⋃ B) – (A ⋂ B)
Also {a, d, c, f} – (A – B) ⋃ (B – A)
(iii) {a, d, c, f, g, h} = (A ⋂ B)’
[∵ {b, e} = A ⋂ B
(i) A ⋃ B
(ii) A’ ⋂ B
(iii) A – B
(iv) B – A
(v) (A ⋃ B)’
(i) A ⋃ B= {a, c, d, e} ⋃ {b, c, e, f}
⇒ A ⋃ B = {a, b, c, d, e, f}
(ii) A’ = {b, f, g, h}
A’ ⋂ B = {b, f, g, h} ⋂ {b, c, e, f}
⇒ A’ ⋂ B = {b, f}
(iii) A - B = {a, c, d, e} – {b, c, e, f}
⇒ A – B = {a, d}
(iv) B – A = {b, c, e, f} – {a, c, d, e}
= {b, f}
(v) A ⋃ B = {a, b, c, d, e, f}
∴ (A ⋃ B)’ = {h, g}
2. From the given diagram, find:
(i) A’
(ii) B’
(iii) A’ ⋃ B’
(iv) (A ⋃ B)’
Also, verify if A’ ⋂ B’ = (A ⋃ B)’.
Solution
(i) A = {1, 3, 4, 6}
∴ A’ = {2, 5, 7, 8, 9, 10}
(ii) B = {1, 2, 5}
∴ B’ = {3, 4, 6, 7, 8, 9, 10}
(iii) A’ ⋃ B’ = {2, 5, 7, 8, 9, 10} ⋃ {3, 4, 6, 7, 8, 9, 10}
= {2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) A ⋂ B = {1, 3, 4, 6} ⋂ {1, 2, 5}
= {1}
∴ (A ⋂ B)’ = {2, 3, 4, 5, 6, 7, 8, 9, 10}
From part (iii) and part (iv) we conclude
A’ ⋃ B’ = (A ⋂ B)’
Now A ⋂ B = {2, 5, 7, 8, 9, 10} ⋂ {3, 4, 6, 7, 8, 9, 10}
⇒ A’ ⋂ B’ = {7, 8, 9, 10} ...(i)
Now A ⋃ B = {1, 3, 4, 6} ⋃ {1, 2, 5}
= {1, 2, 3 4, 5, 6}
∴ (A ⋃ B’) = {7, 8, 9, 10} …(ii)
From I and II we conclude
A’ ⋃ B’ = (A ⋂ B)’
3. Use the given diagram to find:
(i) A ⋃ (B ⋂ C)
(ii) B – (A – C)
(iii) A – B.
(iv) A ⋂ B’
Is A ⋂ B’ = A – B?
(i) B ⋂ C = {d, e, f, g, h, j} ⋂ {h, i, j, k, l}
= {h, j}
∴ A ⋃ (B ⋂ C) = {a, b, c, d, g, h, i} ⋃ {h, j}
= {a, b, c, d, g, h, I, j}
(ii) A – C = {a, b, c, d, g, h, i} – {h, i, j, k, l}
= {a, b, c, d, g}
∴ B – (A – C) = {d, e, f, g, h, j} – {a, b, c, d, g}
= {e, f, h, j}
(iii) A – B = {a, b, c, d, g, h, i} – {d, e, f, g, h, i}
⇒ A – B = {a, b, c, i}
(iv) B’ = {a, b, c, i, k, l, m, n, p}
A ⋂ B’= {a, b, c, d, g, h, i} ⋂ {a, b, c, I, k, l, m, n, p}
⇒ A ⋂ B’ = {a, b, c, i} …..II
From I and II we can conclude A ⋂ B’ = A – B
4. Use the given Venn – diagram to find:
(i) B – A
(ii) A
(iii) B’
(iv) A ⋂ B
(v) A ⋃ B
(i) B – A = {1, 5} – {1, 5, 6, 7, 9}
= { }
(ii) A = {1, 5, 6, 7, 9}
(iii) B = {1, 5}
∴ B’ = {2, 3, 4, 6, 7, 8, 9, 10}
(iv) A ⋃ B = {1, 5, 6, 7, 9} ⋃ {1, 5}
= {1, 5, 6, 7, 9}
5. Draw a Venn – diagram to show the relationship between two overlapping sets A and B. Now shade the region representing:
(i) A ⋂ B
(ii) A ⋃ B
(iii) B – A
Solution
(i) A ⋂ B =
(ii) A ⋃ B =
(iii) B – A =
6. Draw a Venn –diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing:
(i) A ⋃ B
(ii) B’ ⋂ A
(iii) A ⋂ B
(iv) (A ⋃ B)’
Solution
(i) A ⋃ B =
(ii) B’ ⋂ A =
(iii) A ⋂ B =
(iv) (A ⋃ B)’
7. Two set A and B are are such that A ⋂ B = ɸ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing:
(i) A ⋃ B
(ii) (A ⋃ B)’
(iii) B - A
(iv) B ⋂ A’
Solution
(i) A ⋃ B =
(ii) (A ⋃ B)’ =
(iii) B – A
(iv) B ⋂ A’ =
8. State the sets represented by the shaded portion of following venn-diagrams:
(i)
(i) (A ⋃ B)’
(ii) B – A or A’ ⋃ B
(iii) (B - A)’
9. In each of the given diagrams, shade the region which represents the set given underneath the diagram:
(i)
Solution
(i) (B – A) =
(ii) (A ⋂ B)’ =
(iii) (P ⋃ Q)’ =
10. From the given diagram, find:
(i) (A ⋃ B) – C(ii) B – (A ⋂ C)
(iii) (B ⋂ C) ⋃ A
Verify:
A – (B ⋂ C) = (A – B) ⋃ (A – C)
(i) A ⋃ B = {a, b, c, d} ⋃ {c, d, e, g}
= {a, b, c, d, e, g}
∴ (A ⋃ B) – C = {a, b, c, d, e, g} – {b, c, e, f}
= {a, d, g}
(ii) A ⋂ C = {a, b, c, d} ⋂ {b, c, e, f}
= {b, c}
∴ B – (A ⋂ C) = {c, d, e, g} – {b, c}
= {d, e, g}
(iii) B ⋂ C = {c, e, d, g} ⋂ {b, c, e, f}
= {c, e}
11. Using the given diagram, express the following sets in the terms of A and B.
(i) {a, d}
(ii) {a, d, c, f}
(iii) {a, d, c, f, g, h}
(iv) {a, d, g, h}
(v) {g, h}
(i) {a, d} = {a, b, e, d} – {b, c, e, f}
= A – B
(ii) {a, d, c, f} = (A ⋃ B) – {b, e}
= (A ⋃ B) – (A ⋂ B)
Also {a, d, c, f} – (A – B) ⋃ (B – A)
(iii) {a, d, c, f, g, h} = (A ⋂ B)’
[∵ {b, e} = A ⋂ B
∴ (A ⋂ B)’ = {a, d, c, f, g, h}]
(iv) {a, d, g, h} = B’
[∵ {b, c, e, f} = B
(iv) {a, d, g, h} = B’
[∵ {b, c, e, f} = B
∴ B’ = {a, d, g, h}]
(v) {g, h} = (A ⋃ B)’
[∴ A ⋃ B = {a, b, c, d, e, f}
(v) {g, h} = (A ⋃ B)’
[∴ A ⋃ B = {a, b, c, d, e, f}
∴ (A ⋃ B)’ = {g, h}